基于实例的学习
文章目录
- 基于实例的学习
- 1 基本概念与最近邻方法
- 2 K-近邻(KNN)
- 3 距离加权 KNN
- 4 基于实例/记忆的学习器
- 5 局部加权回归
- 5 多种回归方式对比
- 6 懒惰学习与贪婪学习
动机:人们通过 记忆和行动来推理学习。
1 基本概念与最近邻方法
-
名词概念
-
参数化
设定一个特定的函数形式
优点:简单,容易估计和解释
可能存在很大的偏置:实际的数据分布可能不遵循假设的分布
-
非参数化:
分布或密度的估计是数据驱动的(data-driven)
需要事先对函数形式作的估计相对更少
-
-
基于实例的学习
无需构建模型一仅存储所有训练样例,直到有新样例需要分类才开始进行处理。
-
一个概念 c i c_i ci 可以表示为:
样例的集合 c i = e i 1 , e i 2 . . . c_i={e_{i1},e_{i2}...} ci=ei1,ei2...
一个相似度估计函数 f f f
一个阈值 θ \theta θ
-
一个实例 a a a 属于概念 c i c_i ci,当
a a a 和 c i c_i ci 中的某些 e j e_j ej 相似,并且 f ( e i , a ) > θ f(e_i,a)>\theta f(ei,a)>θ
-
-
最近邻方法
计算新的样例和每个样例的距离,找出最近距离的确定其分类。
距离度量:欧式距离 ∑ i = 1 n ( x i − y i ) 2 \sqrt{\sum_{i=1}^n(x_i-y_i)^2} ∑i=1n(xi−yi)2
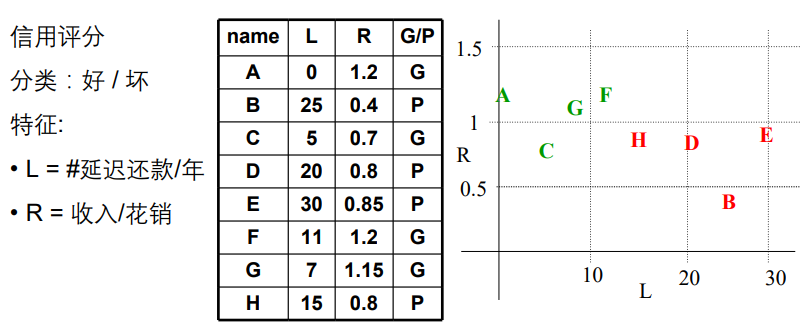
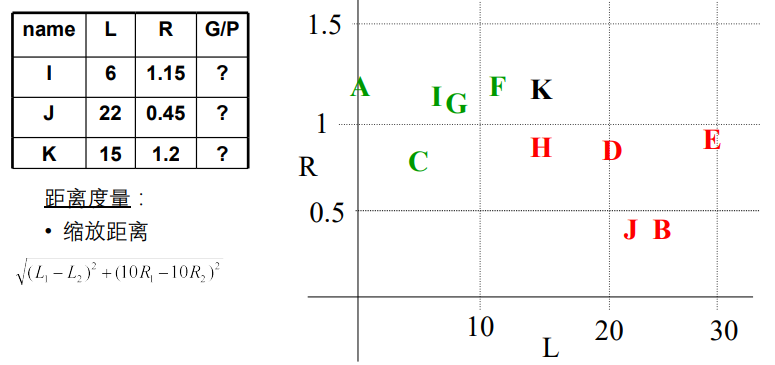
1-NN的错误率不大于Bayes方法错误率的2倍
-
最近邻的点是噪音怎么办?
用不止一个邻居,在邻居中进行投票→K近邻(KNN)
2 K-近邻(KNN)
-
距离度量
-
闵可夫斯基距离(Minkowski Distance)
这是一种广义的距离度量,它包含了欧氏距离、曼哈顿距离和切比雪夫距离等特例
d ( x , y ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 p d (x,y) = \left (\sum_{i=1}^n |x_i - y_i|^p \right )^{\frac {1} {p}} d(x,y)=(i=1∑n∣xi−yi∣p)p1
其中, x x x 和 y y y 是两个 n n n 维向量, x i x_i xi 和 y i y_i yi 是它们的第 i i i 个分量, p p p 是一个正数,表示距离的幂次。当 p = 2 p=2 p=2 时,就是欧氏距离;当 p = 1 p=1 p=1 时,就是曼哈顿距离;当 p = ∞ p=\infty p=∞ 时,就是切比雪夫距离。 -
欧氏距离(Euclidean Distance)
这是最常用的距离度量,它表示两个点在空间中的直线距离,计算公式为:
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 d (x,y) = \sqrt {\sum_{i=1}^n (x_i - y_i)^2} d(x,y)=i=1∑n(xi−yi)2
其中, x x x 和 y y y 是两个 n n n 维向量, x i x_i xi 和 y i y_i yi 是它们的第 i i i 个分量。 -
曼哈顿距离(Manhattan Distance)
又称街区距离,这是另一种常用的距离度量,它表示两个点在网格中的路径距离,计算公式为:
d ( x , y ) = ∑ i = 1 n ∣ x i − y i ∣ d (x,y) = \sum_{i=1}^n |x_i - y_i| d(x,y)=i=1∑n∣xi−yi∣
其中, x x x 和 y y y 是两个 n n n 维向量, x i x_i xi 和 y i y_i yi 是它们的第 i i i 个分量。 -
切比雪夫距离(Chebyshev Distance)
又称棋盘距离,这是一种极端的距离度量,它表示两个点在各个维度上的最大差值,计算公式为:
d ( x , y ) = max i = 1 n ∣ x i − y i ∣ d (x,y) = \max_{i=1}^n |x_i - y_i| d(x,y)=i=1maxn∣xi−yi∣
其中, x x x 和 y y y 是两个 n n n 维向量, x i x_i xi 和 y i y_i yi 是它们的第 i i i 个分量。 -
加权欧氏距离(Mean Censored Euclidean)
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2 n d (x,y) = \sqrt {\frac{\sum_{i=1}^n (x_i - y_i)^2}{n}} d(x,y)=n∑i=1n(xi−yi)2
在欧式距离中,如果维度很高那么最后的值会很大,加权欧式距离/n考虑的就是这个问题。 -
Bray-Curtis Dist
∑ k ∣ x i k − x j k ∣ ∑ k ( x i k + x j k ) \frac{\sum_k|x_{ik}-x_{jk}|}{\sum_k(x_{ik}+x_{jk})} ∑k(xik+xjk)∑k∣xik−xjk∣
在生物信息学上经常被使用,用来描述生物多样性。
-
-
属性
-
属性归一化
目的是消除不同属性之间的量纲和尺度的影响,使得数据更加统一和规范
归一化方法: log , min − max , s u m \log,\min-\max,sum log,min−max,sum
-
属性加权
无关的属性也会被使用进来,需要根据每个属性的相关性进行加权。
加权方法:互信息
KaTeX parse error: Expected 'EOF', got '&' at position 25: …(X)+H(Y)-H(X,Y)&̲\text{H:熵(entro…
-
-
连续取值目标函数
k个近邻训练样例的均值。
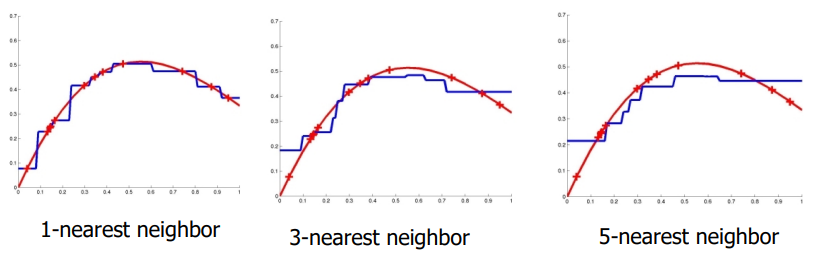
上图中红色:实例的真实值;蓝色:估计值
-
k的选择
-
多数情况下k=3
-
取决于训练样例的数目——更大的k不一定带来更好的效果
-
交叉验证
Leave-one-out:每次拿一个样例作为测试,所有其他的作为训练样例
-
KNN是稳定的——样例中小的混乱不会对结果有非常大的影响
-
-
打破平局
如果k=3并且每个近邻都属于不同的类。
- K值可以稍微比类别数大1或2,并且为奇数
- 取1-NN(最近邻)
- 随机选一个
-
关于效率
KNN算法把所有的计算放在新实例来到时,实时计算开销大
-
加速对最近邻居的选择
先检验临近的点,忽略比目前找到最近的点更远的点
-
通过 KD-tree 来实现
KD-tree: k 维度的树(数据点的维度是 k)
基于树的数据结构
递归地将点划分到和坐标轴平行的方形区域内
-
-
KD-Tree
-
构建 KD-Tree
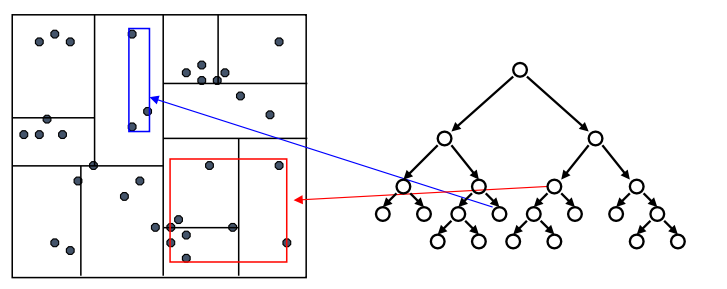
- 选择一个范围最宽的维度,选择一个切分点,根据该维度的数据的中位数,将数据集分成两个子集,使得切分点左边的数据都小于等于它,右边的数据都大于等于它;
- 递归地对左子树和右子树重复上述步骤,直到剩余的数据点少于 m,或者区域的宽度达到最小值
- 返回根节点,完成 KD-Tree 的构建。
在每个叶节点维护一个额外信息:这个节点下所有数据点的 (紧) 边界
-
查询
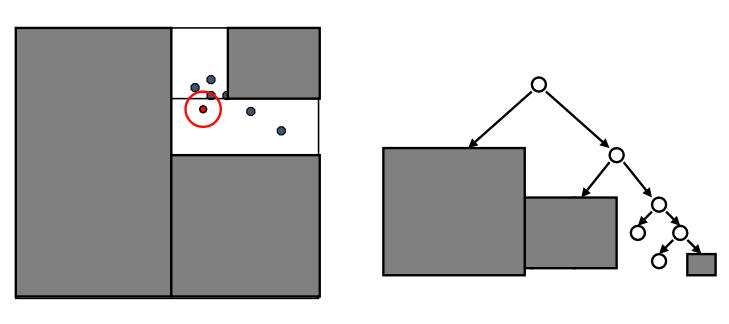
-
先检验临近的点:关注距离所查询数据点最近的树的分支
-
达到一个叶节点后:计算节点中每个数据点距离目标点的距离
-
接着回溯检验我们访问过的每个树节点的另一个分支,每次找到一个最近的点,就更新距离的上界
-
利用最近距离以及每个树节点下数据的边界信息,对一部分不可能包含最近邻居的分支进行剪枝
-
-
-
KNN 优缺点
-
优点:
-
概念上很简单,但可以处理复杂的问题
-
通过对k-近邻的平均,对噪声数据更鲁棒
-
容易理解:预测结果可解释
-
训练样例中呈现的信息不会丢失,样例本身被显式地存储下来
-
实现简单、稳定、没有参数(除了 k)
-
-
缺点
- 内存开销大:需要存储所有样例
- CPU 开销大:分类新样本需要更大时间
- 很难确定一个合适的距离函数
- 不相关的特征 对距离的度量有负面的影响
-
3 距离加权 KNN
-
加权函数
w i = K ( d ( x i , x q ) ) w_i=K(d(x_i,x_q)) wi=K(d(xi,xq))
其中 d ( x i , x 1 ) d(x_i,x_1) d(xi,x1)是查询数据点与 x i x_i xi 之间的关系; K ( ⋅ ) K(·) K(⋅) 是决定每个数据点权重的核函数。 -
输出
predict = ∑ w i y i ∑ w i \text{predict}=\frac{\sum w_iy_i}{\sum w_i} predict=∑wi∑wiyi -
对比加权前后效果
-
KNN
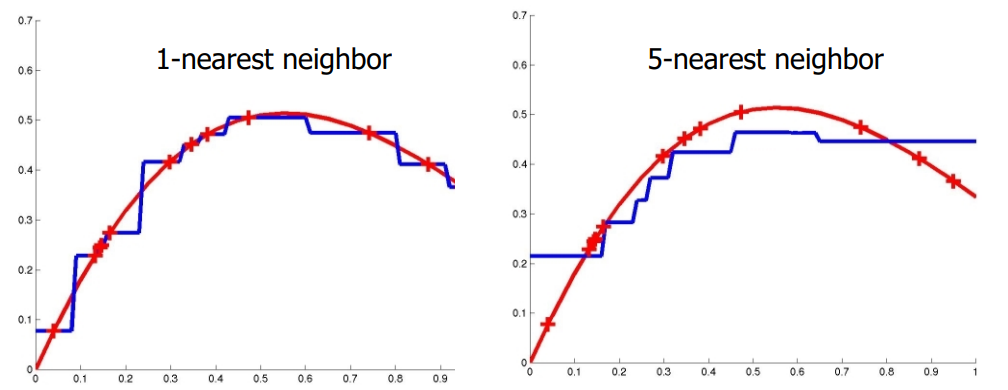
-
距离加权KNN
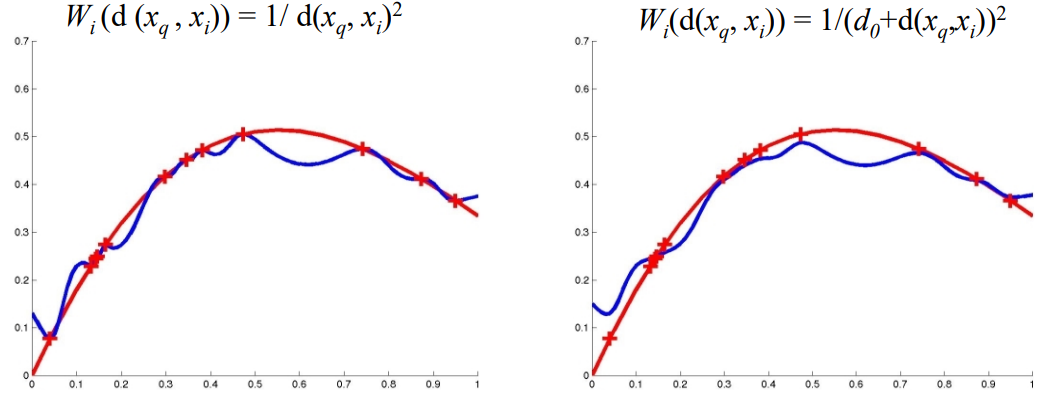
高斯核函数:曲线更加平滑。

-
4 基于实例/记忆的学习器
- 1-NN
- 距离度量:欧式距离
- 使用多少个邻居:一个
- 加权函数(加权):无
- 如何使用已知的邻居节点:和邻居节点相同
- K-NN
- 距离度量:欧式距离
- 使用多少个邻居:K 个
- 加权函数(加权) :无
- 如何使用已知的邻居节点:K 个邻居节点投票
- 距离加权 KNN
- 距离度量:缩放的欧式距离
- 使用多少个邻居:所有的,或K 个
- 加权函数(加权) :高斯核函数
- 如何使用已知的邻居节点:每个输出的加权平均
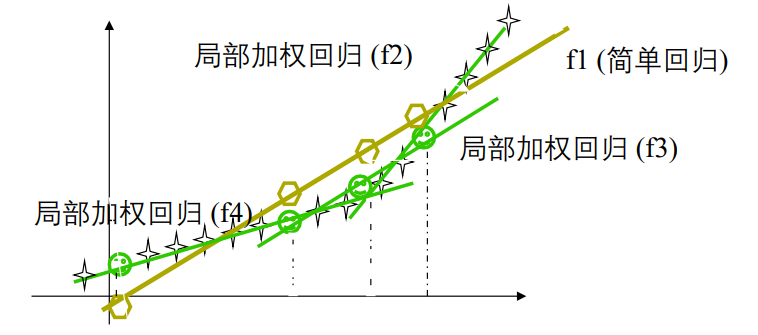
5 局部加权回归
-
距离度量:缩放的欧式距离
-
使用多少个邻居:所有的,或K 个
-
加权函数(加权) :高斯核函数
-
如何使用已知的邻居节点:首先构建一个局部的线性模型。拟合 β 最小化局部的加权平方误差和
β = arg min β ∑ k = 1 N w k 2 ( y k − β ⊤ X k ) 2 \beta = \mathop{\arg\min}_\beta \sum_{k=1}^Nw_k^2(y_k-\beta^\top X_k)^2 β=argminβk=1∑Nwk2(yk−β⊤Xk)2
5 多种回归方式对比
-
线性回归
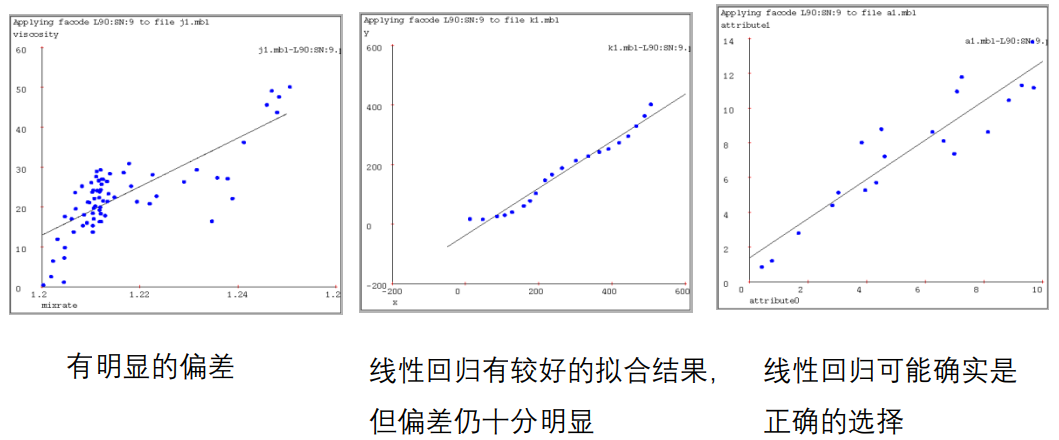
-
连接所有点
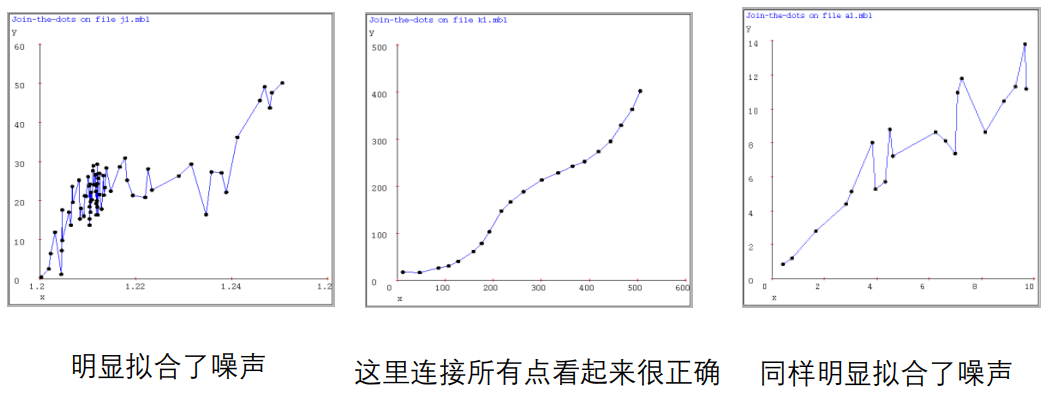
-
1-近邻
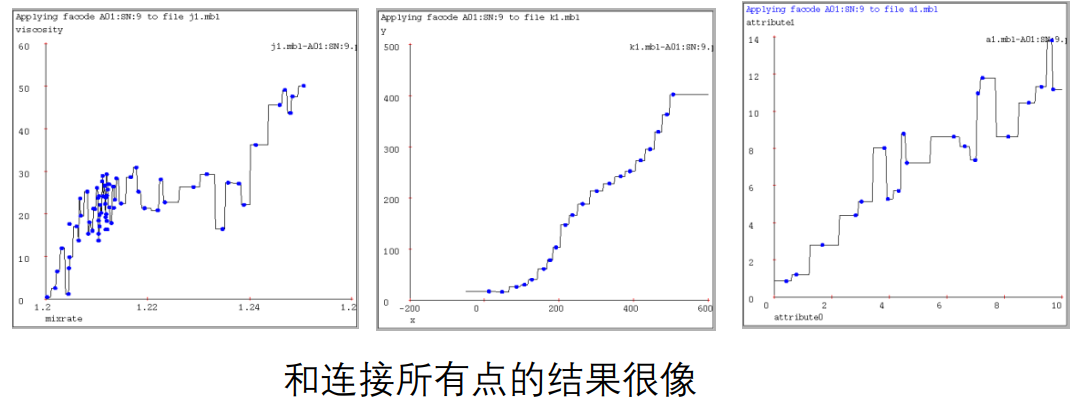
-
k-近邻(k=9)
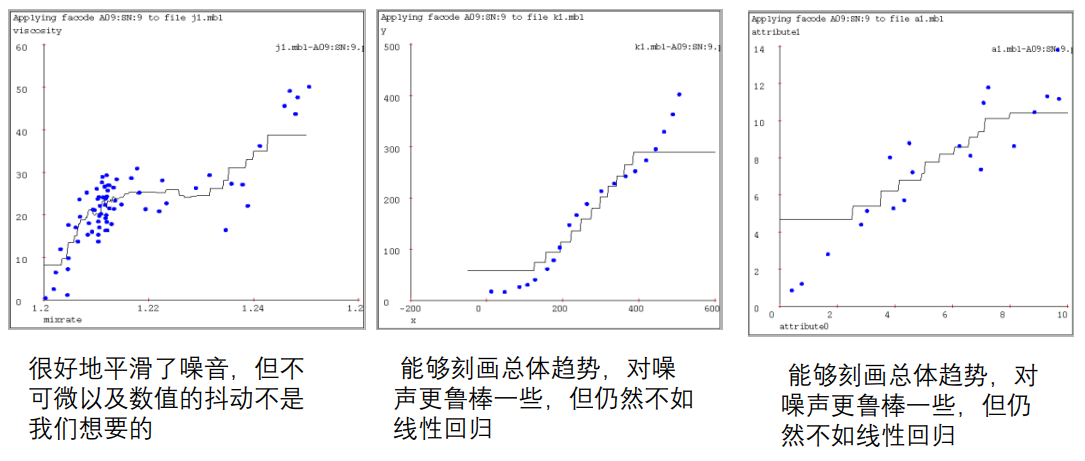
-
距离加权 KNN(核回归)
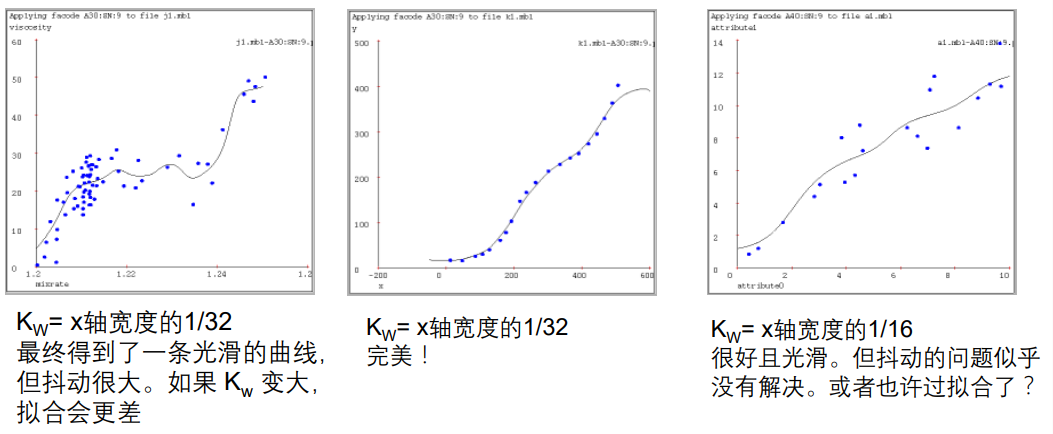
选择一个合适的 K w K_w Kw 非常重要,不仅是对核回归,对所有局部加权学习器都很重要。
-
局部加权回归
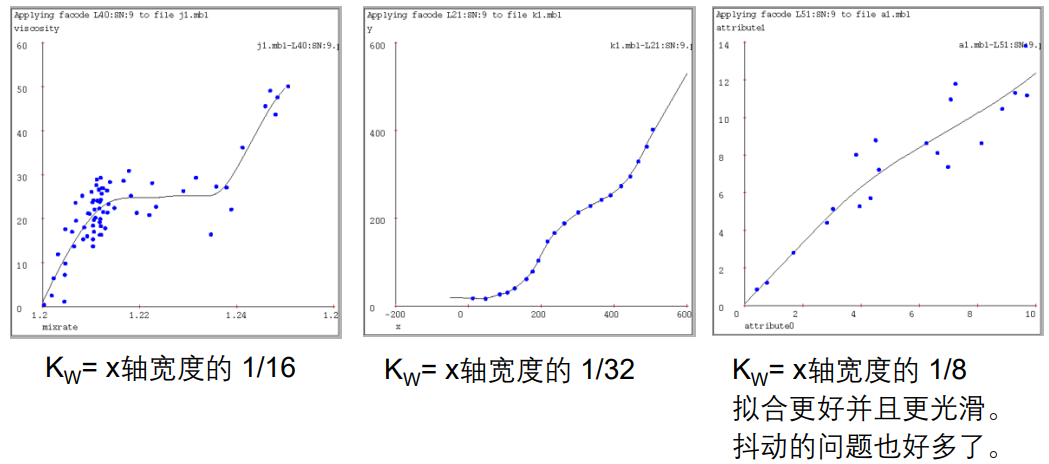
6 懒惰学习与贪婪学习
- 贪婪学习:查询之前就泛化
- 训练时间长,测试时间短
- 对于每个查询使用相同模型,倾向于给出全局估计
- 懒惰学习:等待查询再泛化
- 训练时间短,测试时间长
- 可以得到局部估计
如果它们共享相同的假设空间,懒惰学习可以表示更复杂的函数





![[word] word如何打印背景和图片? #微信#其他#经验分享](https://img-blog.csdnimg.cn/img_convert/8e46bdb2025f7b692459ac16f8ff36d8.jpeg)