回归分析：研究X和Y之间相关性的分析

回归分析是数据分析中最基础也是最重要的分析工具，绝大多数的数据分析问题，都可以使用回归的思想来解决。回归分析的任务就是，通过研究自变量X和因变量Y的相关关系，尝试去解释Y的形成机制，进而达到通过X去预测Y的目的。

三个关键词: 相关性 X：自变量 Y：因变量 （X:解释变量 Y：被解释变量） 相关性 ≠ 因果性

连续值型变量 0-1型变量 定序遍历 计数变量 生存变量

在实际应用中，Y常常是我们需要研究的那个核心变量。

（1）经济学家研究经济增长的决定因素，那么Y可以选取GDP增长率（连续数值型变量）。

（2）P2P公司要研究借款人是否能按时还款，那么Y可以设计成一个二值变量，Y=0时代表可以还Y=1时代表不能还款（0‐1型变量）。

（3）消费者调查得到的数据（1表示非常不喜欢，2表示有点不喜欢，3表示一般般，4表示有点喜欢，5表示非常喜欢）（定序变量）。

（4）管理学中RFM模型：F代表一定时间内，客户到访的次数，次数其实就是一个非负的整数。（计数变量）

（5）研究产品寿命、企业寿命甚至是人的寿命（这种数据往往不能精确的观测，例如现在要研究吸烟对于寿命的影响，如果选取的样本中老王60岁，现在还活的非常好，我们不可能等到他去世了再做研究，那怎么办呢？直接记他的寿命为60+，那这种数据就是截断的数据）（生存变量）

回归分析的使命：

使命1：回归分析要去识别并判断：哪些X变量是同Y真的相关，哪些不是。统计学中有一个非常重要的领域，叫做“变量选择”。（逐步回归法）

使命2：去除了那些同Y不相关的X变量，那么剩下的，就都是重要的、有用的X变量了。接下来回归分析要回答的问题是：这些有用的X变量同Y的相关关系是正的呢，还是负的？

使命3：在确定了重要的X变量的前提下，我们还想赋予不同X不同的权重，也就是不同的回归系数，进而我们可以知道不同变量之间的相对重要性。

这就是回归分析要完成的三个使命：

第一、识别重要变量；

第二、判断相关性的方向；

第三、要估计权重（回归系数）。

回归分析的分类：

数据的分类：

横截面数据 ： 在某一时点收集的不同对象的数据

例如：

（1）我们自己发放问卷得到的数据

（2）全国各省份2018年GDP的数据

（3）大一新生今年体测的得到的数据

时间序列数据：对同一对象在不同时间连续观察所取得的数据。

例如：

（1）从出生到现在，你的体重的数据（每年生日称一次)。

（2）中国历年来GDP的数据。

（3）在某地方每隔一小时测得的温度数据。

面板数据：横截面数据与时间序列数据综合起来的一种数据资源。

例如：

2008‐2018年，我国各省份GDP的数据。

不同数据类型的处理方法：

建模比赛中，前两种数据类型最常考到；面板数据较为复杂，是经管类学生在中级计量经济学中才会学到的模型。

横截面数据往往可以使用回归来进行建模，我们通过回归可以得到自变量与因变量之间的相关关系以及自变量的重要程度。

时间序列数据往往需要进行我们进行预测，时间序列模型的选择也很多，大家需要选择合适的模型对数据进行建模

数据的收集：

因为提供数据的网站容易失效，所以大家可以直接在知乎上搜索“数据查找”来获取最新的数据网站

一元线性回归：

线性假定并不要求初始模型都呈上述的严格线性关系，自变量与因变量可通过变量而转化成线性模型

使用线性回归模型进行建模前，需要对数据进行预处理。用Excel、Matlab、Stata等软件都可以

回归系数的解释：

可以看到，引入了新的自变量价格后，对回归系数的影响非常大！！！

原因：遗漏变量导致的内生性

内生性的探究：

包含了所有与y相关，但未添加到回归模型中的变量

如果这些变量和我们已经添加的自变量相关，则存在内生性

核心解释变量和控制变量：

无内生性（no endogeneity）要求所有解释变量均与扰动项不相关。这个假定通常太强，因为解释变量一般很多（比如，5‐15个解释变量），且需要保证它们全部外生。

是否可能弱化此条件？答案是肯定的，如果你的解释变量可以区分为核心

解释变量与控制变量两类。

核心解释变量：我们最感兴趣的变量，因此我们特别希望得到对其系数的一致估计（当样本容量无限增大时，收敛于待估计参数的真值 ）。

控制变量：我们可能对于这些变量本身并无太大兴趣；而之所以把它们也放入回归方程，主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素。

在实际应用中，我们只要保证核心解释变量与𝝁不相关即可。

什么时候取对数：

目前，对于什么时候取对数还没有固定的规则，但是有一些经验法则：

（1）与市场价值相关的，例如，价格、销售额、工资等都可以取对数；

（2）以年度量的变量，如受教育年限、工作经历等通常不取对数；

（3）比例变量，如失业率、参与率等，两者均可；

（4）变量取值必须是非负数，如果包含0，则可以对y取对数ln(1+y);

取对数的好处：（1）减弱数据的异方差性（2）如果变量本身不符合正态分布，取了对数后可能渐近服从正态分布（3）模型形式的需要，让模型具有经济学意义。

四类模型回归系数的解释：

特殊的自变量：虚拟变量X

如果自变量中有定性变量，例如性别、地域等，在回归中要怎么处理呢？

例如：我们要研究性别对于工资的影响(性别歧视）。

为了避免完全多重共线性的影响，引入虚拟变量的个数一般是分类数减1。

可以利用stata软件

拟合优度R的平方较低怎么办：

（1）回归分为解释型回归和预测型回归。

预测型回归一般才会更看重𝑅的平方 。

解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著

性即可。

（2）可以对模型进行调整，例如对数据取对数或者平方后再进行回归。

（3）数据中可能有存在异常值或者数据的分布极度不均匀。

补充：关于拟合优度和调整后的拟合优度：

我们引入的自变量越多，拟合优度会变大。但我们倾向于使用调整后的拟合优度，

如果新引入的自变量对SSE的减少程度特别少，那么调整后的拟合优度反而会减小。（可以放在论文中）

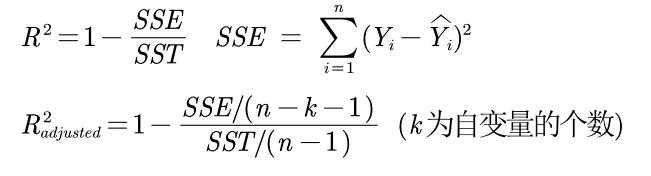
标准化回归系数：

为了更为精准的研究影响评价量的重要因素（去除量纲的影响）

我们可考虑使用标准化回归系数。

对数据进行标准化，就是将原始数据减去它的均数后，再除以该变量的标准差，计算得到新的变量值，新变量构成的回归方程称为标准化回归方程，回归后相应可得到标准化回归系数。

标准化系数的绝对值越大，说明对因变量的影响就越大（只关注显著的回归系数哦）。

扰动项要满足的条件：

在之前的回归分析中，我们都默认了扰动项是球型扰动项。

球型扰动项：满足“同方差”和“无自相关”两个条件。

横截面数据容易出现异方差的问题；时间序列数据容易出现自相关的问题。

异方差：

如果扰动项存在异方差：

（1）OLS估计出来的回归系数是无偏、一致的。

（2）假设检验无法使用（构造的统计量失效了）。

（3）OLS估计量不再是最优线性无偏估计量（BLUE）。

注意：这里的信息和熵权法里面确定权重时的信息不是一个意思。异方差这里出现的信息可以理解为对于模型的稳定程度所做的贡献，异方差是指各个扰动项的方差不相同，那么方差较大的扰动项破坏模型稳定性的程度就较大，我们就说它包含的信息量减少。而在熵权法中，方差越大，说明这个指标对于不同个体而言的变化程度就大，那么我们在评价时就不能轻易忽视这个变量。

怎么解决异方差：

（1）使用OLS + 稳健的标准误

（2）广义最小二乘估计法GLS

原理：方差较小的数据包含的信息较多，我们可以给予信息量大的数据更大的权

重（即方差较小的数据给予更大的权重）

拟合值出现负数的原因：

有75%的奶粉品牌的评价量小于1109，评价量超过17000的只有10%不到，而样本均值却达到了15800。这说明评价量的分布极度不平衡，大多数个体的评价量都较小。从右图中也直观的说明了绝大部分品牌的评价量都较小这一特征。

逐步回归分析：

向前逐步回归Forward selection： 将自变量逐个引入模型，每引入一个自变量后都要进行检验，显著时才加入回归模型。

(缺点：随着以后其他自变量的引入，原来显著的自变量也可能又变为不显著了，但是，并没有将其及时从回归方程中剔除掉。)

向后逐步回归Backward elimination： 与向前逐步回归相反，先将所有变量均放入模型，之后尝试将其中一个自变量从模型中剔除，看整个模型解释因变量的变异是否有显著变化，之后将最没有解释力的那个自变量剔除；此过程不断迭代，直到没有自变量符合剔除的条件。（缺点：一开始把全部变量都引入回归方程，这样计算量比较大。若对一些不重要的变量，一开始就不引入，这样就可以减少一些计算。当然这个缺点随着现在计算机的能力的提升，已经变得不算问题了）

逐步回归的说明：