今日主要总结一下动态规划的一道题目,583. 两个字符串的删除操作
题目:583. 两个字符串的删除操作
Leetcode题目地址
题目描述:
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
示例 1:
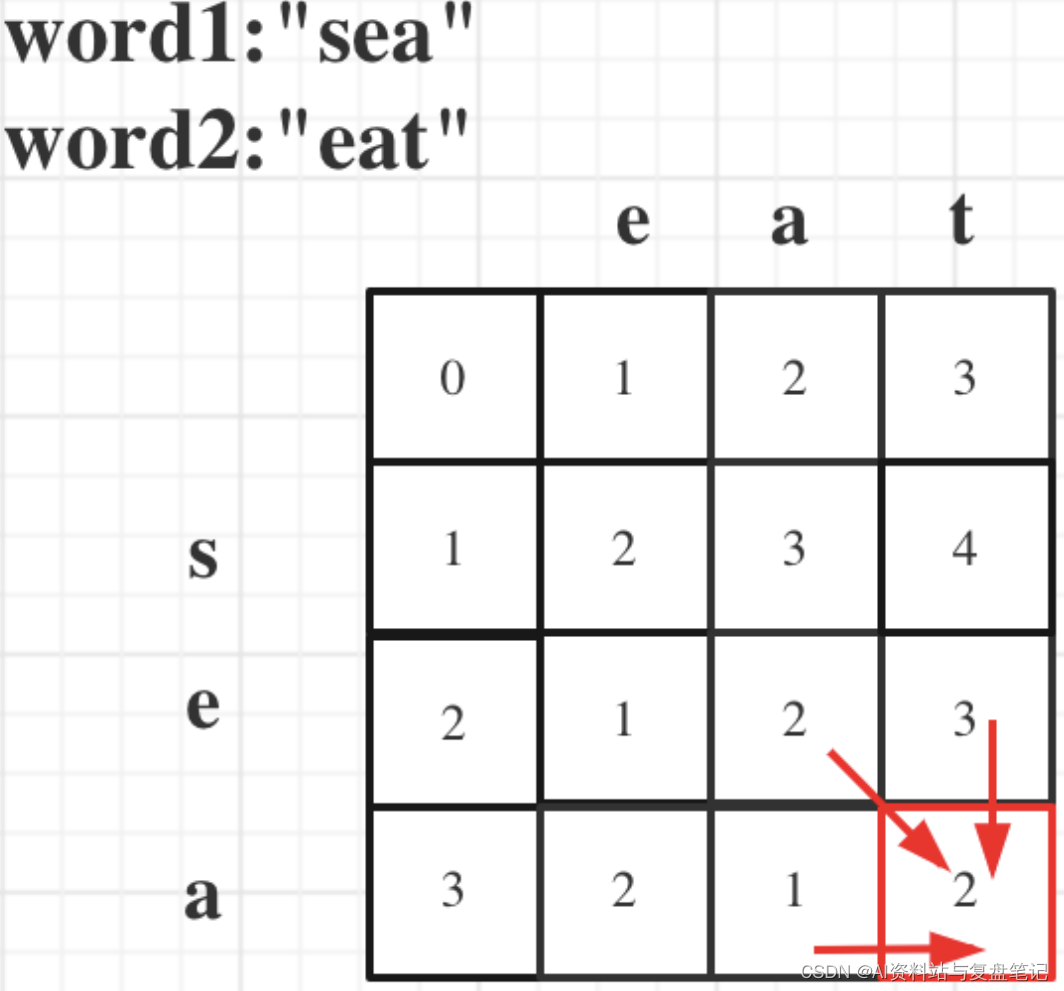
输入: word1 = “sea”, word2 = “eat”
输出: 2
解释: 第一步将 “sea” 变为 “ea” ,第二步将 "eat "变为 “ea”
示例 2:
输入:word1 = “leetcode”, word2 = “etco”
输出:4
提示:
1 <= word1.length, word2.length <= 500
word1 和 word2 只包含小写英文字母
动态规划方法一:
本题和一文搞懂动态规划之115. 不同的子序列问题相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。
这次是两个字符串可以相互删了,这种题目也知道用动态规划的思路来解,动规五部曲,分析如下:
-
确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
这里dp数组的定义有点点绕,大家要撸清思路。 -
确定递推公式
当word1[i - 1] 与 word2[j - 1]相同的时候
当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
因为dp[i - 1][j - 1] + 1等于 dp[i - 1][j] 或 dp[i][j - 1],所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1); -
dp数组如何初始化
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
dp[0][j]的话同理,所以代码如下:
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
-
确定遍历顺序
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。 -
如果有什么问题别忘记打印dp数组
C++代码
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>>dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for(int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j <= word2.size(); j++){
if(word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
else{
dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2));
}
}
}
return dp[word1.size()][word2.size()];
}
};
动态规划方法二:
另一个比较巧妙的思路就是本题和一文搞懂动态规划之1143. 最长公共子序列问题基本相同,只要求出两个字符串的最长公共子序列长度即可,那么除了最长公共子序列之外的字符都是必须删除的,最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。
C++代码
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>>dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
for(int i = 1; i <= word1.size(); i++){
for(int j = 1; j <= word2.size(); j++){
if(word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()];
}
};
总结
动态规划
英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的
对于动态规划问题,可以拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
本题提供了两种动态规划的思路解法:
-
解法一和一文搞懂动态规划之115. 不同的子序列问题相比,其实就是两个字符串都可以删除了,情况虽说复杂一些,但整体思路是不变的。
-
解法二的思路就是本题和一文搞懂动态规划之1143. 最长公共子序列问题基本相同,只要求出两个字符串的最长公共子序列长度即可,那么除了最长公共子序列之外的字符都是必须删除的,最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。
本题其实是动规解决的经典题目,我们只要想到 用二维数组可以记录两个字符串的所有比较情况,这样就比较好推导递推公式了!
欢迎大家关注本人公众号:编程复盘与思考随笔
(关注后可以免费获得本人在csdn发布的资源源码)