一、gumbel-softmax的使用

gumbel-softmax里面的 $\tau$值越接近无穷获得的向量越接近一个均匀分布的向量；$\tau$值越接近0获得的向量越接近一个one-hard vector；$\tau$值越接近1则gumbel-softmax就和softmax越类似

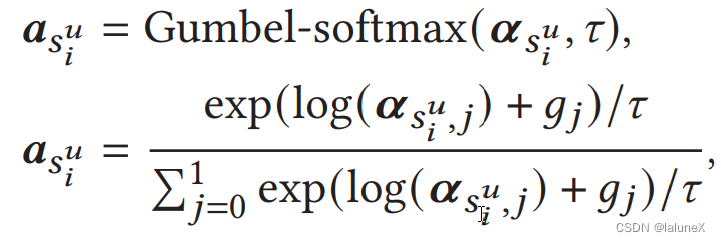
# score：代表序列内每个item的sorce，这里的分数不是one-hard的，需要gumbel来将其转化为one-hard vector，batchsize*max_seq_len*2
# mask：这个序列的mask矩阵，batchsize*max_seq_len*1
# gumbel_tau：温度参数

mask = mask.squeeze()

# 获得one-hard vector的score，batchsize*max_seq_len*2
score_gumbel_softmax = F.gumbel_softmax(score, tau=self.gumbel_tau, hard=True)

# 获取序列每个item的neg_flag和pos_flag
neg_flag = score_gumbel_softmax[:, :, 1] * mask
pos_flag = (1 - neg_flag) * mask

二、课程学习的使用

这里用到了课程学习（从易到难），最后得到经过课程学习筛选的loss和。因为我们是从易到难，所以是先删除loss较大的值，然后再逐步减小被删除值的个数。 当然也可以从难到易，代码同从易到难

r"""
loss_list：重构loss，batchsize*max_seq_len
drop_rate：课程学习的μ，代表需要删除比例
"""

# 将整个序列loss的最后一维进行升序排序
# loss_list_sorted代表被排序好的值
# loss_index_sorted代表被排序的loss值的索引
loss_list_sorted, loss_index_sorted = torch.sort(loss_list, descending=False, dim=-1)

# 获得loss的保留率
remind_rate = 1 - drop_rate

# 获得需要保留多少个loss
remind_num = int(remind_rate * len(loss_list))

# 先删除loss较大的值，保留loss较小的值
processed_loss_list_sorted = loss_list_sorted[:remind_num]

# 将获得的loss相加，获得这一个batch里面的loss总和
recommender_ce_loss = torch.sum(processed_loss_list_sorted)

三、有监督的对比学习的使用

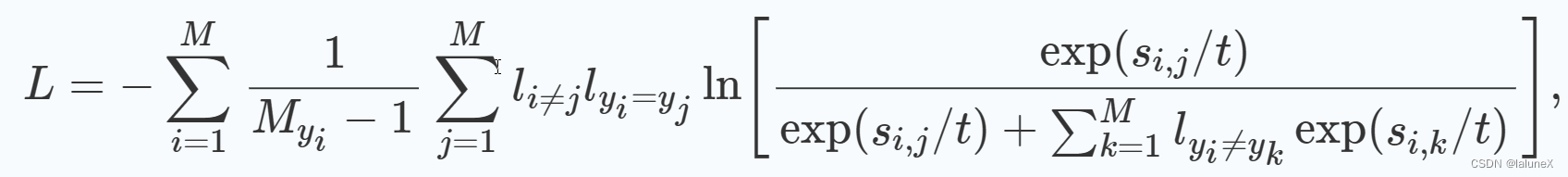
上图为有监督的对比学习，而下面的代码是我根据有监督的对比学习和推荐项目进行修改的版本，具体公式为：
$\mathcal{L}=-\sum _{i=1}^M\frac{1}{M_{y_i}-1}\sum _{j=1}^P{l}_{y_j=+}\ln \left(\frac{\exp \left(\text{sim}\left(s_i,s_j\right)/\tau \right)}{\exp \left(\text{sim}\left(s_i,s_j\right)/\tau \right)+\sum _{k=1}^P{l}_{y_j=-}\exp \left(\text{sim}\left(s_i,s_k\right)/\tau \right)}\right)$
这里的P是句子的长度

# seq_emb：
# item_seq_emb：序列的emb，batsize*max_seq_len*feat_dim
# item_pos_flag：序列内正样本的mask
# mask：序列的mask矩阵
# tau：温度参数

item_seq_emb = item_seq_emb * mask

target_seq_emb = seq_emb.unsqueeze(1).expand_as(
    item_seq_emb
).to(torch.float)
# 这步得到它的相似度矩阵
similarity_matrix = F.cosine_similarity(item_seq_emb, target_seq_emb, dim=2)

# 这步给相似度矩阵求exp, 并且除以温度参数T, 注意要乘mask
similarity_matrix_after_exp = torch.exp(similarity_matrix / tau) * mask.squeeze()

# 这步产生了正样本（五噪音item）的相似度矩阵，其他位置都是0
sim = item_pos_flag * similarity_matrix_after_exp

# 用原先的相似度矩阵减去正样本矩阵得到负样本（噪音item）的相似度矩阵
no_sim = similarity_matrix_after_exp - sim
# 把负样本矩阵按行求和，得到的是对比损失的分母(还差一个与分子相同的那个相似度，后面会加上)
no_sim_sum = torch.sum(no_sim, dim=1, keepdim=True)

'''
将上面的矩阵扩展一下，再转置，加到sim（也就是正样本矩阵上），然后再把sim矩阵与sim_num矩阵做除法。
至于为什么这么做，就是因为对比损失的分母存在一个正样本的相似度，就是分子的数据。
'''
no_sim_sum_expend = no_sim_sum.expand_as(item_pos_flag)
sim_sum = sim + no_sim_sum_expend

# 为了防止自监督对比学习的分母为0
zero_anomaly_process = sim_sum.le(0.).float() * 1e-10
anomaly_process_sim_sum = sim_sum + zero_anomaly_process

sim_div = torch.div(sim, anomaly_process_sim_sum)

'''
由于loss矩阵中，存在0数值，那么在求-log的时候会出错。这时候，我们就将loss矩阵里面为0的地方
全部加上1，然后再去求loss矩阵的值，那么-log1 = 0 ，就是我们想要的。
'''
sim_div_sum = sim_div + sim_div.eq(0)

# 接下来就是算一个批次中的sup_con_loss了
sim_div_sum_log = -torch.log(sim_div_sum)  # 求-log

# 返回一个一维的张量
sup_con_loss = torch.sum(
    torch.sum(sim_div_sum_log, dim=1) / (torch.sum(item_pos_flag, dim=-1))
)

四、无监督的对比学习的使用

${\mathcal{L}}_{i,j}=-\log \frac{\exp \left(\text{sim}\left({\mathbf{z}}_i,{\mathbf{z}}_j\right)/\tau \right)}{\sum _{k=1,k\ne i}^{2N}\exp \left(\text{sim}\left({\mathbf{z}}_i,{\mathbf{z}}_k\right)/\tau \right)}$
$L=\frac{1}{2N}\sum _{k=1}^N\left[l\left(2k-1,2k\right)+l\left(2k,2k-1\right)\right]$

def contrastiveLoss(
        target_emb,  # (bs, dim)
        class_prototype_emb,    # (class_num, dim)
        prototype_mask,  # (bs, class_num)
        tau,
):
    target_emb_normalize = F.normalize(target_emb, dim=1)  # (bs, dim)  --->  (bs, dim)
    class_prototype_emb_normalize = F.normalize(class_prototype_emb, dim=1)  # (class_num, dim)  --->  (class_num, dim)

    target_seq_emb_repeat = target_emb_normalize.unsqueeze(1).repeat(
        1, class_prototype_emb.shape[0], 1
    ).to(torch.float)   # (bs, class_num, dim)
    class_prototype_emb_repeat = class_prototype_emb_normalize.unsqueeze(0).repeat(
        target_emb.shape[0], 1, 1
    ).to(torch.float)   # (bs, class_num, dim)

    similarity_matrix = F.cosine_similarity(target_seq_emb_repeat, class_prototype_emb_repeat,
                                            dim=2)

    # 这步给相似度矩阵求exp, 并且除以温度参数T, 注意要乘mask
    similarity_matrix_after_exp = torch.exp(similarity_matrix / tau)

    # 这步产生了正样本（五噪音item）的相似度矩阵，其他位置都是0
    sim = prototype_mask * similarity_matrix_after_exp

    # 用原先的相似度矩阵减去正样本矩阵得到负样本（噪音item）的相似度矩阵
    no_sim = similarity_matrix_after_exp - sim

    # 把负样本矩阵按行求和，得到的是对比损失的分母(还差一个与分子相同的那个相似度，后面会加上)
    no_sim_sum = torch.sum(no_sim, dim=1, keepdim=True)

    '''
    将上面的矩阵扩展一下，再转置，加到sim（也就是正样本矩阵上），然后再把sim矩阵与sim_num矩阵做除法。
    至于为什么这么做，就是因为对比损失的分母存在一个正样本的相似度，就是分子的数据。
    '''
    no_sim_sum_expend = no_sim_sum.expand_as(prototype_mask)
    sim_sum = sim + no_sim_sum_expend

    sim_div = torch.div(sim, sim_sum)

    '''
    由于loss矩阵中，存在0数值，那么在求-log的时候会出错。这时候，我们就将loss矩阵里面为0的地方
    全部加上1，然后再去求loss矩阵的值，那么-log1 = 0 ，就是我们想要的。
    '''
    sim_div_sum = sim_div + sim_div.eq(0)

    # 接下来就是算一个批次中的con_loss了
    sim_div_sum_log = -torch.log(sim_div_sum)  # 求-log
    con_loss = torch.sum(
        torch.sum(sim_div_sum_log, dim=1)
    )

    return con_loss

或者使用现成的库

class SupervisedContrastiveLoss(nn.Module):
    def __init__(self, temperature=0.1):
        super(SupervisedContrastiveLoss, self).__init__()
        self.temperature = temperature

    def forward(self, feature_vectors, labels):
        # Normalize feature vectors
        feature_vectors_normalized = F.normalize(feature_vectors, p=2, dim=1)
        # Compute logits
        logits = torch.div(
            torch.matmul(
                feature_vectors_normalized, torch.transpose(feature_vectors_normalized, 0, 1)
            ),
            self.temperature,
        )
        return losses.NTXentLoss(temperature=0.07)(logits, torch.squeeze(labels))

criterion = SupervisedContrastiveLoss(temperature=0.5).to('cuda:0') # Custom Implementation