文章目录

• 计数排序
• 基数排序

计数排序

计数排序也是非比较排序的一种，在之前的博客介绍的都是比较排序，跟之前的比较排序相比计数排序并不是很常用，不常用的原因也是它的局限性耗费空间很大，只能对整数进行排序，并且数据在范围太大的时候计数排序也是不太行。
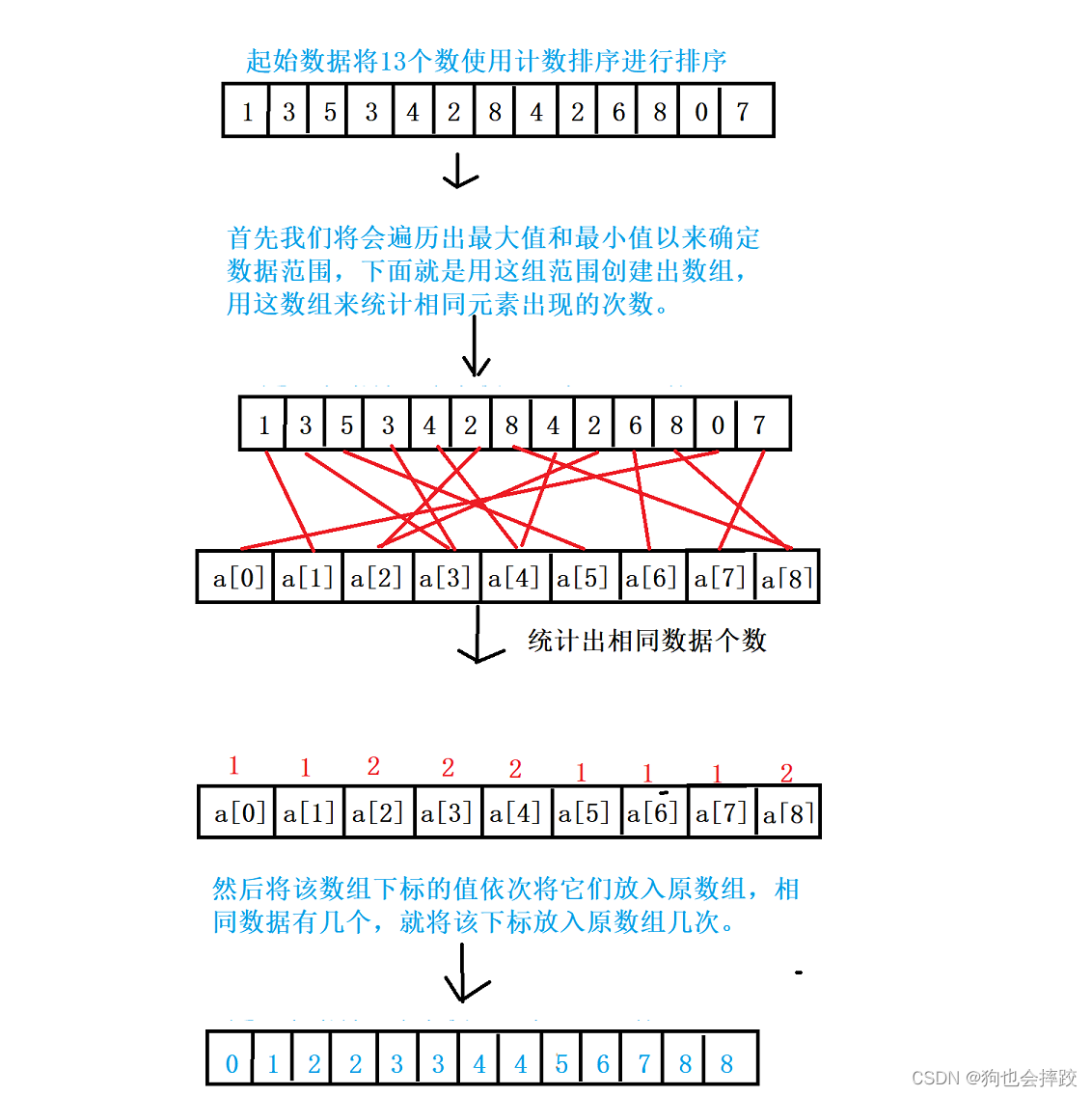
计数排序思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。
操作步骤：

1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
   
   代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

void CountSort(int* a, int n)
{
	int max = a[0];
	int min = a[0];
	for (int i = 1; i < n; i++)
	{
		if (max < a[i])
		{
			max = a[i];
		}
		if (min > a[i])
		{
			min = a[i];
		}
	}
	int range = max - min+1;
	int* tmp = (int* )calloc(range,sizeof(int));
	if (tmp == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	//memset(tmp, 0, range*sizeof(int));

	for (int j = 0; j < n; j++)
	{
		tmp[a[j]-min]++;
	}

	int ret = 0;
	for (int k = 0; k < range; ++k)
	{
		while (tmp[k]--)
		{
			a[ret++] = k + min;
			//tmp[k]--;
		}
	}
	free(tmp);
}

void Print(int *a,int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ",a[i]);
	}
	printf("\n");
}

int main()
{
	int arr[] = {1,5,3,3,5,9,2,5,7,8};
	CountSort(arr,sizeof(arr)/sizeof(int));
	Print(arr,sizeof(arr)/sizeof(int));
	return 0;
}

计数排序的特性总结：

1. 计数排序在数据范围集中时，效率很高，但是适用范围及场景有限。
2. 时间复杂度：O(range(范围)+N)
3. 空间复杂度：O(range(范围))
4. 稳定性：稳定

#############################################################
#############################################################
#############################################################
#############################################################
#############################################################

基数排序

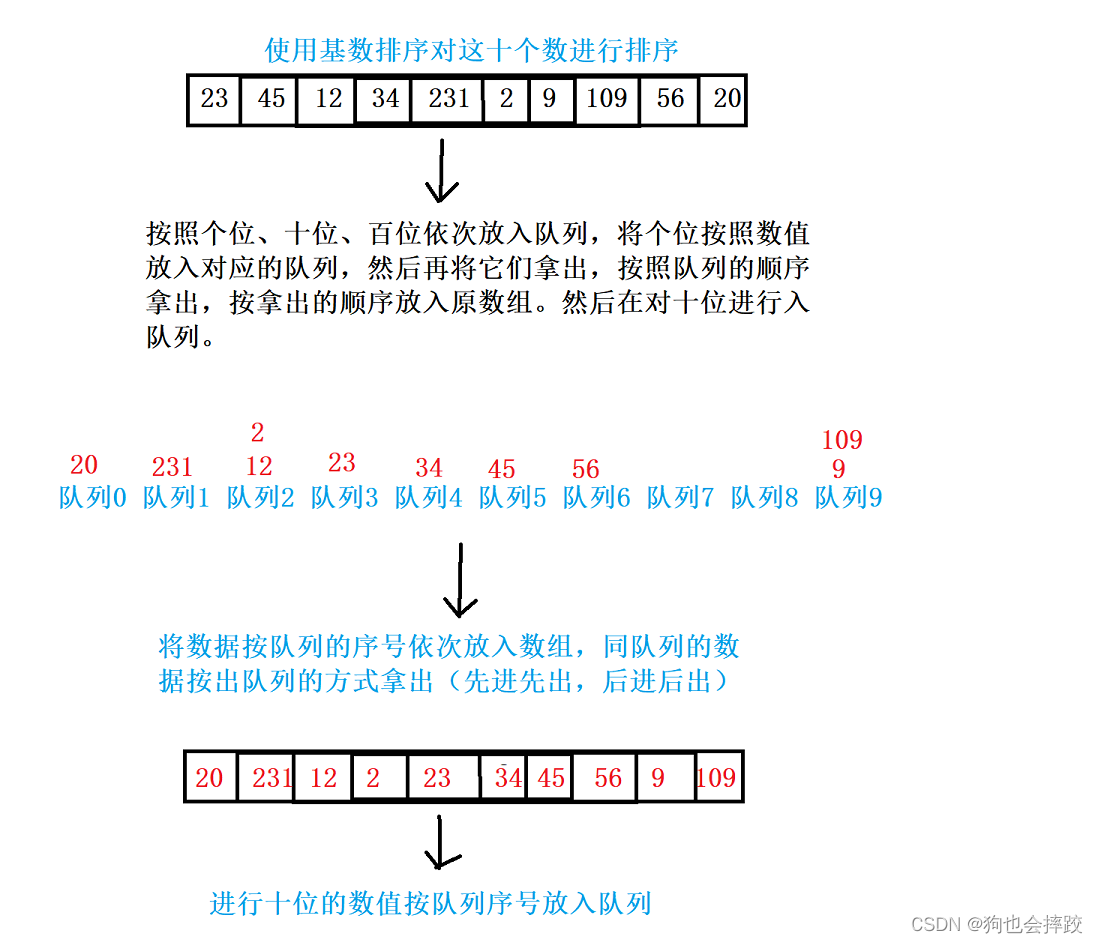
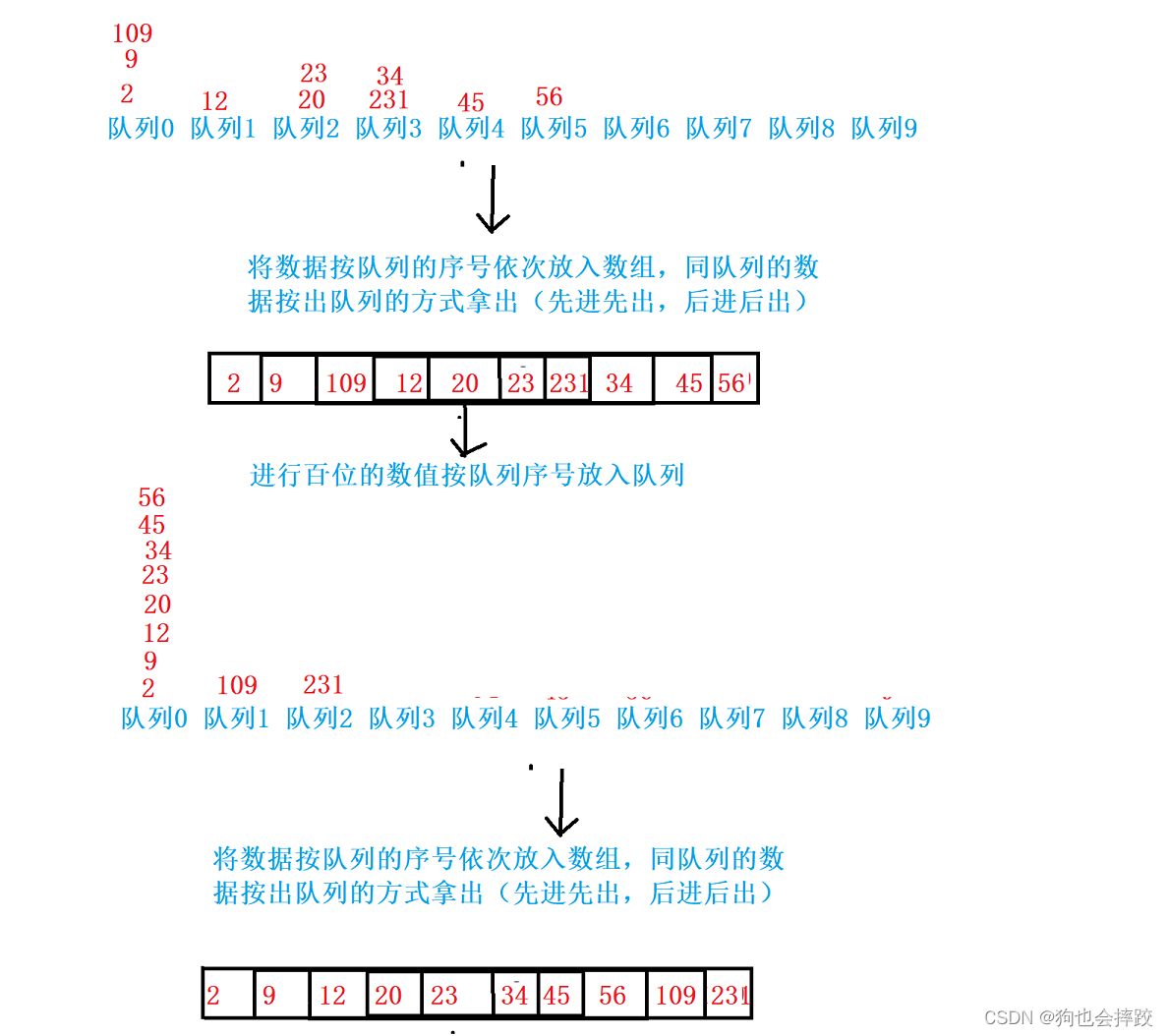
基数和计数排序是属于一类，同样是非交换排序。上面得知计数排序就不是常用的排序，而基数排序比计数排序还不常用，所以在这里只是介绍一下思想，并不展示代码了。
基数排序思想：
这里是需要借助队列，因为所有数字都是由0-9组成的所以这里需要创建十个队列。