引言
数据科学的一个中心假设是,紧密度表明相关性。彼此“接近”的数据点是相似的。如果将年龄、头发数量和体重绘制在空间中,很可能许多人会聚集在一起。这就是 k 均值聚类背后的直觉。
我们随机生成 K 个质心,每个簇一个,并将每个数据点分配给与该数据点最近的质心对应的簇。然后,我们生成新的质心,每个质心都是属于该簇的所有点的平均值。然后重复这个过程直到收敛。
我们可以使用欧几里德距离作为距离度量并计算每个数据点与质心之间的距离。
def cross_euclidean_distance(x, y=None):
y = x if y is None else y
assert len(x.shape) >= 2
assert len(y.shape) >= 2
return euclidean_distance(x[..., :, None, :], y[..., None, :, :])这样我们就可以执行 K 均值聚类算法的核心了。
def fit(self, X):
cluster_ind = np.repeat(0, X.shape[0])
idx = np.random.randint(X.shape[0], size=self.m_clusters)
self.centroids = X.loc[idx].to_numpy()
cross_dist = cross_euclidean_distance(X.to_numpy(), self.centroids)
cluster_ind = np.argmin(cross_dist, axis = 1)
for _ in range(self.max_iter):
#Calculating new centroids
for i in range(self.m_clusters):
X_i = X[cluster_ind == i]
self.centroids[i] = X_i.mean(axis = 0).to_numpy()
#Assigne data points to new cluster and check if cluster assignment chenges
cross_dist = cross_euclidean_distance(X.to_numpy(), self.centroids)
cluster_ind_new = np.argmin(cross_dist, axis = 1)
if not (cluster_ind_new == cluster_ind).any():
break
cluster_ind = cluster_ind_newK-means算法保证收敛,但可能不会收敛到全局最优。相反,它经常陷入局部最优。本文的其余部分将致力于解决这个问题。

根据种子的不同,算法可能会陷入局部最优
关注公众号 [小Z的科研日常] ,查看最新技术分享。
简单的解决方案
最简单的解决方案就是使用不同的起始质心多次运行算法,然后选择最佳的聚类分配。
为了有效地做到这一点,我们需要一种衡量方法来量化集群分配的好坏。其中一种衡量标准是欧几里得畸变。每个点到质心的平均距离对应于它们分配到的簇。运行该算法几次并保存欧几里得失真最低的算法,并希望它是全局最优的。
def euclidean_distortion(X, z):
X, z = np.asarray(X), np.asarray(z)
assert len(X.shape) == 2
assert len(z.shape) == 1
assert X.shape[0] == z.shape[0]
distortion = 0.0
for c in np.unique(z):
Xc = X[z == c]
mu = Xc.mean(axis=0)
distortion += ((Xc - mu) ** 2).sum()
return distortion更智能的采样
幸运的是,我们可以做得更好。这种方法的主要问题是计算成本较高。为了缓解这个问题,我们可以调整起始条件,以便我们更有可能找到全局最优值。为了了解如何实现,让我们看一个玩具问题。

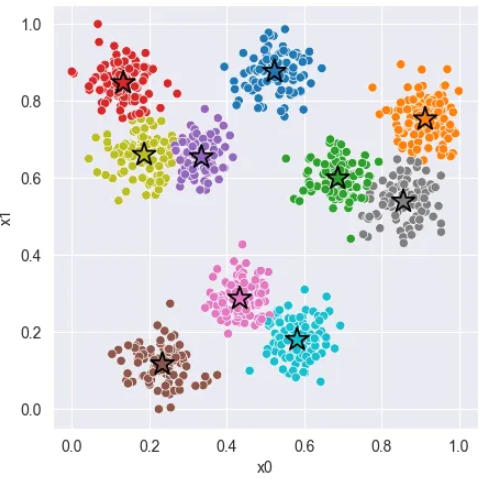
我们希望我们的算法找到总共 10 个数据组。看起来有 10 个不同的簇。当我们运行算法时,我们发现我们可能会得到一个或两个集群错误。

使用 K = 10 运行 K 均值聚类后的聚类分配。我们看到分配并不完美。紫色簇太大,而黄色和青绿色簇争夺同一组。
两个组成为一个超级集群,而另一个组则由两个集群共享。发生这种情况可能是因为两个初始质心靠得太近。为了减少这种情况发生的可能性,我们可以在如何对初始质心进行采样方面变得更加智能。
我们可以不从数据中均匀采样质心,而是从加权分布中顺序采样质心,其中每个权重由到已采样质心的距离决定。这确保了我们不太可能对接近已采样质心的质心进行采样。其算法很简单。在这里,我简单地将概率视为每个数据点到最近质心的归一化距离。这确保我们不会对同一个数据点进行两次采样。
idx = np.random.choice(range(X.shape[0]), size=1)
centroids = X.loc[idx].to_numpy()
while len(centroids)<self.m_clusters:
distances = cross_euclidean_distance(centroids, X.to_numpy())
prob_vec = distances.min(axis = 0)
prob_vec = prob_vec**2/np.sum(prob_vec**2)
#Note: zero proability that new centorid is allready a centroid
idx = np.append(idx, np.random.choice(X.shape[0], size=1, p = prob_vec))
centroids = X.loc[idx].to_numpy()
self.centroids = centroids智能分配
然而,上述方法可能仍然有些不足。我们只是增加了不出现错误初始配置的机会。为了确保我们得到全局最大值的分配,我们仍然需要运行算法多次。这样做的问题是,每次重新启动算法时,我们都会丢弃进度。更好的方法是找出我们当前任务的问题所在以及如何改进。考虑这个集群分配。

这个簇分配非常糟糕,有两个超级簇和两对质心,彼此距离太近。
黄色和青绿色的簇占据了太多的空间,而棕色、紫色、粉色和橙色的簇则占据了很少的空间。通过智能分配算法,我们可以识别两个最近的质心,并将其中一个移动到最需要的位置。
也就是说,到距质心最远的点。如果我们进行了太多的跳跃,我们只需保存最佳的收敛统计数据,就像之前的重复过程一样。这个的实现是在下面的代码中完成的。
n_worst = int(round(X.shape[0]*self.worst_prec))
best_reroll_centroids = self.centroids
best_reroll_distortion = euclidean_distortion(X, cluster_ind)
for i in range(self.n_rerolls):
# Caculate new centroids
for i in range(self.m_clusters):
X_i = X[cluster_ind == i]
self.centroids[i] = X_i.mean(axis = 0).to_numpy()
# Find the two centroids that are closest and pick the centoid with the lowest average distance to other centroids
centroid_dist = cross_euclidean_distance(self.centroids)
cetorid_dist_inf = centroid_dist + np.diag(np.repeat(np.inf, centroid_dist.shape[0])) # Add inf to diag
worst_pair = np.unravel_index((cetorid_dist_inf).argmin(), cetorid_dist_inf.shape) # Find indexes of worst pair
worst_ind = worst_pair[0] if (np.mean(centroid_dist[worst_pair[0]])<np.mean(centroid_dist[worst_pair[1]])) else worst_pair[1]
# Assign the old centroid to be the one closest to the poinst that are furthest away from the current centroids
min_dists = np.min(cross_dist, axis = 1)
high_dists_ind = np.argpartition(min_dists, -n_worst)[-n_worst:]
X_high = X.loc[high_dists_ind]
self.centroids[worst_ind] = X_high.mean(axis = 0).to_numpy()
# Itterate until convergence
for _ in range(self.max_iter):
#Calculating new centroids
for i in range(self.m_clusters):
X_i = X[cluster_ind == i]
self.centroids[i] = X_i.mean(axis = 0).to_numpy()
#Assigne data points to new cluster and check if cluster assignment chenges
cross_dist = cross_euclidean_distance(X.to_numpy(), self.centroids)
cluster_ind_new = np.argmin(cross_dist, axis = 1)
if not (cluster_ind_new == cluster_ind).any():
break
cluster_ind = cluster_ind_new
distortion = euclidean_distortion(X, cluster_ind)
if distortion<best_reroll_distortion:
best_reroll_distortion = distortion
best_reroll_centroids = self.centroids
self.centroids = best_reroll_centroids 下图显示了正在运行的算法。首先,粉红色的簇被移动。

粉红色的质心已经跳到绿松石色的星团上
我们看到粉红色的质心已经跳到绿松石色的星团上。此配置仍远未达到最佳状态。紫色和粉红色的簇所占的量太少,而黄色和绿松石色的簇所占的量太多。这可以通过重复该过程几次来解决。

可以观察到紫色质心跳到粉色簇

可以观察到紫色质心跳转到黄色质心
通过最后的跳跃,我们可以简单地运行直到收敛,最终获得接近最佳的集群分配。


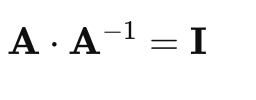



![[ESP32 IDF]web server](https://img-blog.csdnimg.cn/direct/486795c983a341e69b62f562d1de125d.png)
