一、说明

        机器学习是一个引人入胜的领域，它使计算机能够从数据中学习并做出预测或决策，而无需明确编程。然而，在幕后，有一个坚实的数学和线性代数基础，构成了机器学习算法的支柱。在本文中，我们将探讨在深入研究机器学习之前应该熟悉的关键数学概念和线性代数基础知识。

二、机器学习的数学：

2.1. 微积分：

        微积分在理解机器学习基础的优化算法方面起着至关重要的作用。梯度下降是一种广泛使用的优化算法，它依赖于函数的导数。让我们举一个简单的例子：

f（x） = x²

为了找到导数 f′（x），我们可以使用 Python：

import sympy as sp

x = sp.symbols('x')
f = x**2
derivative = sp.diff(f, x)
print("Derivative of f(x) =", derivative)

        这将输出导数 f′（x）=2x。微积分帮助我们了解函数如何变化并指导机器学习中的优化过程。

2.2. 概率与统计：

        概率和统计是机器学习的支柱，特别是在理解不确定性、分布和根据数据做出明智的决策方面。例如，正态分布的概率密度函数：

Python 允许我们使用 NumPy 和 SciPy 等库处理概率分布。

概率密度函数

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

mu, sigma = 0, 1
x = np.linspace(-5, 5, 1000)
plt.plot(x, norm.pdf(x, mu, sigma))
plt.title('Normal Distribution')
plt.show()

三、机器学习中的线性代数：

线性代数是机器学习的语言，提供有效理解和操作数据的工具。

3.1. 向量和矩阵：

向量和矩阵是线性代数的构建块。向量可以表示为：

矩阵如下：

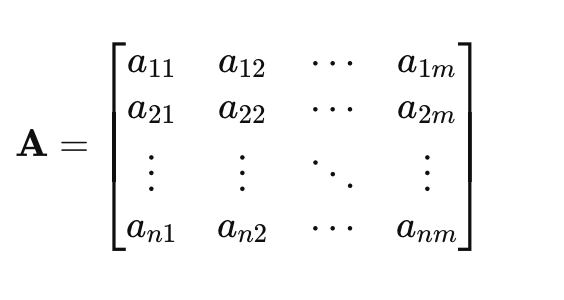
3.2. 矩阵乘法：

矩阵乘法是机器学习中的一项基本操作。给定两个矩阵 A 和 B，乘积 C = A ⋅ B 计算公式为：

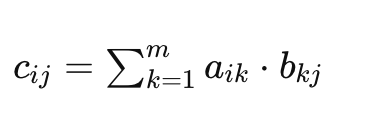
矩阵乘法

让我们在 Python 中实现它：

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

C = np.dot(A, B)
print("Matrix Multiplication Result:")
print(C)

3.3. 特征分解：

        特征分解是另一个关键概念。给定一个方阵 A，它可以分解为其特征值 （λ） 和特征向量 （v）：

Av= λv

        这通常用于降维技术，如主成分分析 （PCA）。

四、导数和梯度下降：

        我们之前讨论过寻找导数，现在让我们在梯度下降的上下文中使用导数。梯度下降是一种优化算法，用于迭代最小化函数。例如：

f（x） = x³− 3x² + 2x + 1

        我们可以通过使用梯度迭代更新 x 来找到最小值：

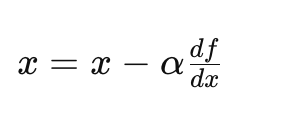
        减去梯度

其中 α 是学习率。让我们在 Python 中实现它：

import sympy as sp

x = sp.symbols('x')
f = x**3 - 3*x**2 + 2*x + 1
derivative = sp.diff(f, x)

# Gradient Descent
alpha = 0.1
x_val = 2  # Initial value of x
iterations = 10

for _ in range(iterations):
    x_val = x_val - alpha * derivative.subs(x, x_val)

print("Minimum value of f(x) at x =", x_val)

4.1. 集成：

        积分是另一个基本概念，特别是在概率等领域，其中积分概率密度函数给出累积分布函数。让我们集成一个简单的函数：

∫（ 3x²+ 2x ）dx

integral_result = sp.integrate(3*x**2 + 2*x, x)
print("Integral result =", integral_result)

4.2. 求解方程：

        求解方程是一项常见的任务，尤其是在线性代数和优化中。让我们求解一个简单的方程：

2x+5=0

solution = sp.solve(2*x + 5, x)
print("Solution for 2x + 5 =", solution)

4.3. 矩阵反转：

        矩阵反演对于求解线性方程组至关重要。给定矩阵 A 及其逆矩阵 A−，乘积应为单位矩阵 I：

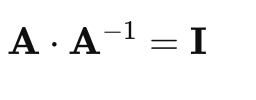
        让我们在 Python 中演示一下：

A = np.array([[2, 1], [1, 3]])
A_inv = np.linalg.inv(A)
identity_matrix = np.dot(A, A_inv)

print("Original Matrix A:")
print(A)
print("\nInverse of A:")
print(A_inv)
print("\nProduct of A and A_inv (should be the identity matrix):")
print(identity_matrix)

五、结论：

        坚实的数学和线性代数基础对于任何潜入机器学习的人来说都是必不可少的。了解用于优化的微积分、用于处理数据不确定性的概率和统计以及用于高效数据操作的线性代数是释放机器学习算法全部潜力的关键。Python 凭借其丰富的库生态系统，提供了一个强大的平台，可以在机器学习的背景下实现和试验这些数学概念。祝您学习愉快！