一、题目描述
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值 0 代表空单元格;
- 值 1 代表新鲜橘子;
- 值 2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例
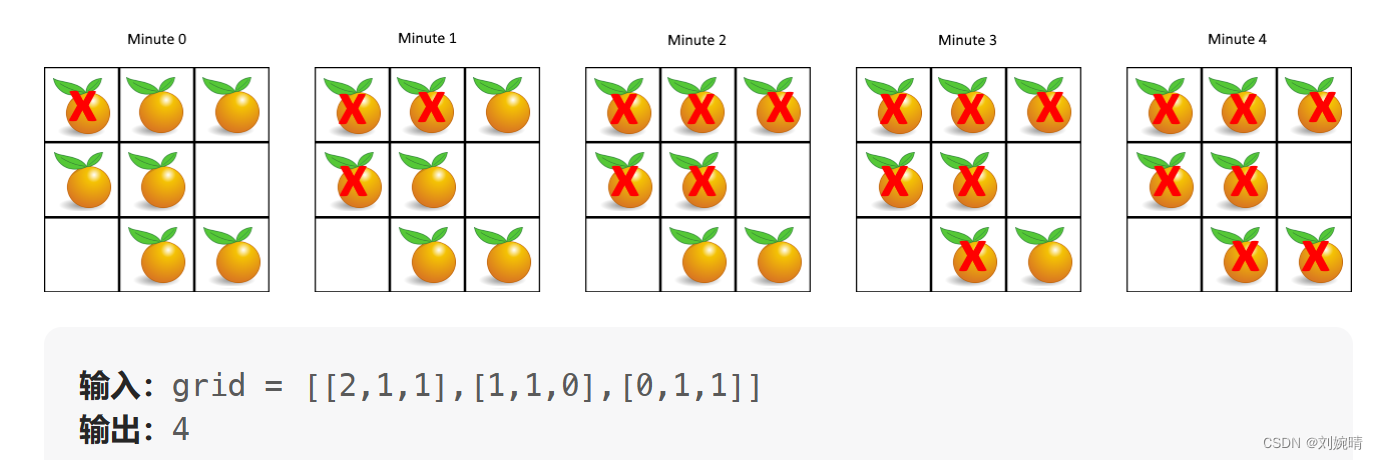
二、思路
总体思路 —— 肯定是对每个感染的橘橘,向四周感染,因此是广度优先搜索遍历
问题转化 ——求最短感染时间 ? nonono~~ 求的是 共可以感染多少层 后结束 (这就是最短时间)
代码实现思路: ——
- 我们第一次把所有感染的橘子放在一起加入队列中,作为第一层
- 然后我们把第一层的每个橘橘向四周感染,然后把第一层的橘橘移除队列,把感染后的橘橘加入队列,作为第二层
- 对每一层的橘橘,如果其能向四周感染至少一个橘橘,就把结果 count++ (结果计数)—— 然后把这一层的感染橘橘的四周都感染一遍
- 重复上述步骤,直至队列为空
- 队列为空说明不能再往下感染了,然后我们判断还有没有没感染的橘橘,这样的橘橘永远不会被感染到(幸运的橘橘~~)
图解:

三、代码实现
1. 一些巧思
(1)队列中存放的元素
对存放每一层感染橘橘的队列,我们应该存放的是感染橘橘的坐标,但是这样很占用空间,因此优化如下:
—— 队列中元素为:temp = i * n + j ,其中 i 为橘橘所在行,j 为橘橘所在列,n 为每列多少个元素
—— 根据 i * n + j 反推得到当前橘橘所在的行与列
i = temp / n;
j = temp % n;
(2) 向当前感染橘橘四周搜索的代码
我们得到了当前的感染橘橘坐标为 x , y ,对向其四周搜索我们完全可以写四个方向,但是这样非常复杂,因此我们可以定义如下坐标跃迁数组:
int[] rowStep = {-1, 1, 0, 0}; // 上下走
int[] colStep = {0, 0, -1, 1}; // 左右走
这样在向四周遍历时,我们就可以通过如下的方式得到四个方向的坐标,并对其进行判断和相应操作:
// 向四周遍历
for(int k=0; k<4; k++){
// 得到当前要遍历的坐标
int x = xTemp + rowStep[k];
int y = yTemp + colStep[k];
if(x>=0 && x<m && y>=0 && y<n){ // 保证得到的坐标不越界
// 相应操作
// .....
}
}
2. 完整代码
题外话: 写这个代码时候,往二叉树的层次遍历去想,嘿嘿嘿,太像了不是嘛,就是一模一样鸭,就是对每层进行操作,二叉树的层次遍历是对每层中元素操作其左右节点,这个是操作其四周的节点,一模一样,一模一样了~
// 994. 腐烂的橘子
public int orangesRotting(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0;
int[] rowStep = {-1, 1, 0, 0}; // 上下走
int[] colStep = {0, 0, -1, 1}; // 左右走
// 初始化队列 —— 第一层
Queue<Integer> queue = init(grid);
// 广度优先搜索
while(!queue.isEmpty()){
// 当前层感染的橘橘数量
int size = queue.size();
// 是否含有新鲜的橘橘可以被感染
boolean hasFresh = false;
// 对当前层的每个感染的橘橘, 把它的周围都感染一圈
for(int i=0; i<size; i++){
int temp = queue.poll();
int xTemp = temp / n;
int yTemp = temp % n;
// 感染该橘橘的上下左右
for(int k=0; k<4; k++){
int x = xTemp + rowStep[k];
int y = yTemp + colStep[k];
if(x>=0 && x<m && y>=0 && y<n){
if(grid[x][y] == 1){
hasFresh = true; // 有可以感染的橘橘
grid[x][y] = 2;
queue.offer(x * n + y);
}
}
}
}
if(hasFresh) res += 1; // 有可以感染的橘橘才结果才加一
}
if (hasFreshFinal(grid)) return -1;
return res;
}
// 队列初始化 —— 加入所以感染的橘橘作为第一层
public Queue<Integer> init(int[][] grid){
Queue<Integer> queue = new LinkedList<>();
int m = grid.length;
int n = grid[0].length;
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
if(grid[i][j] == 2){
queue.add(i * n + j);
}
}
}
return queue;
}
// 判断最后还有没有没感染的橘橘
public Boolean hasFreshFinal(int[][] grid){
int m = grid.length;
int n = grid[0].length;
for(int i=0; i<m; i++){
for(int j=0; j<n; j++){
if(grid[i][j] == 1){
return true;
}
}
}
return false;
}