8. 第 1 讲(选修):反向传播_哔哩哔哩_bilibili
Gradient Descent
neual work基本架构已经学过了
backpropagation(反向传播)可以帮助我们有效的进行渐变迭代计算(帮助计算梯度)。
假设网络有一大堆参数:
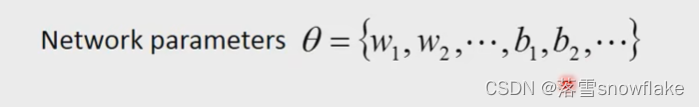
首先选一个初始的参数,

然后计算对 Loss function的gradient

也就是计算每一个loss function中的参数,如下:

计算出这个vector之后更新参数:

如何有效的计算出 vector,就是用backpropagation。

唯一有效的是backparopagation,它其中比较高深的就是数学Chain Rule。
Chain Rule
case1 假设有2个function,y=g(x),z=h(y), x会影响y,y会影响z

case2 如图三个函数,其中s的变化影响x和y,x和y的变化影响z。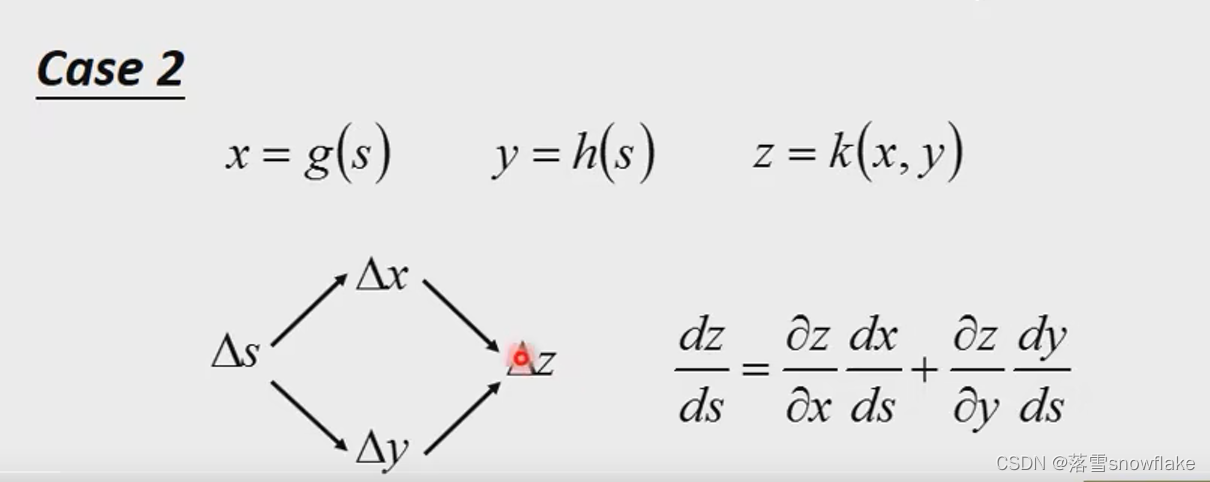
第一种情况下,一元复合函数求导,内部求导与外部求导的乘积。
第二种情况下,多元复合函数求导,划分求导路径,不同路径求导后加和就行了。
回到neual work training
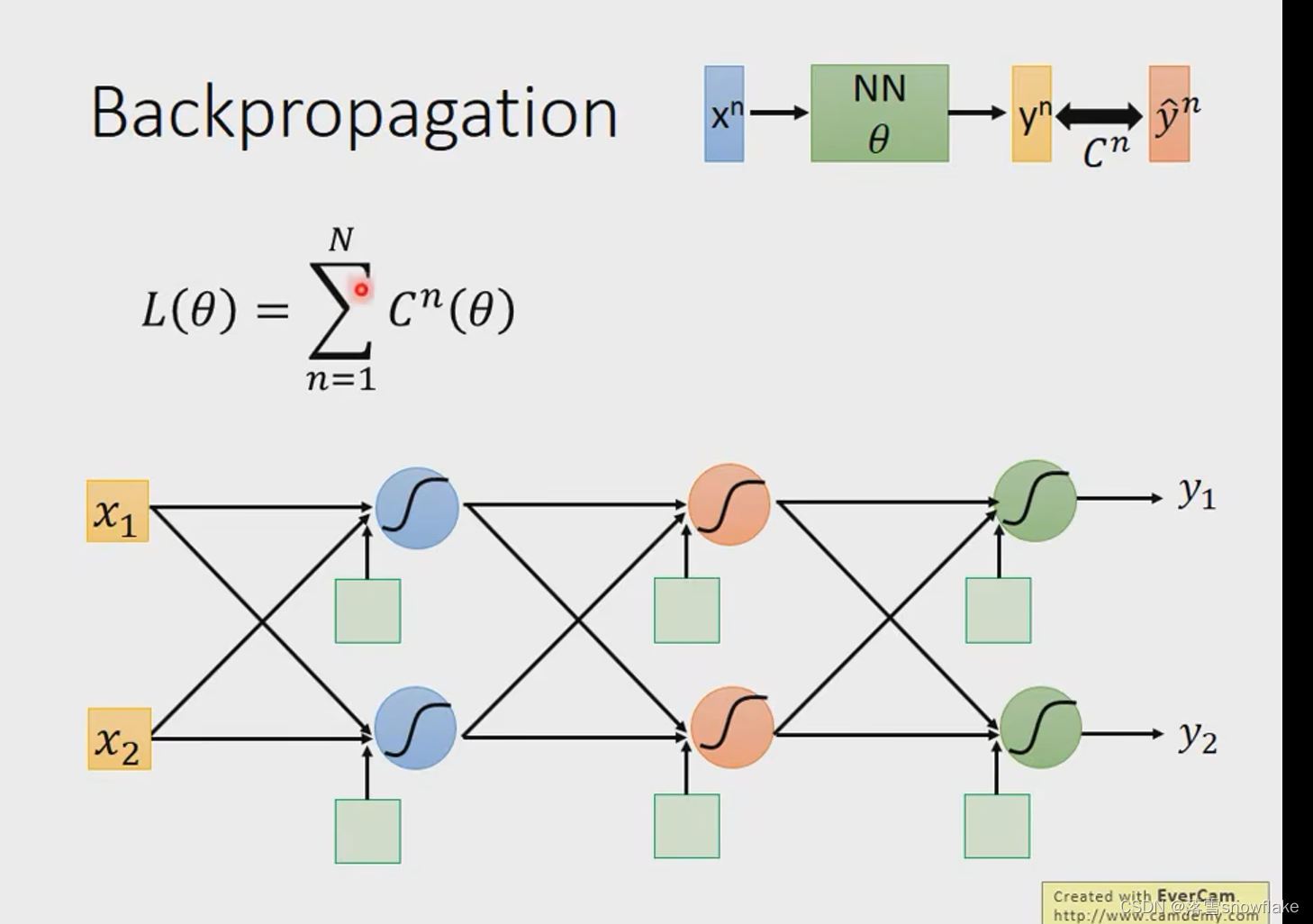
定义一个loss,看图中的Loss Function,是求和所有trainning data的某一个loss值c,

j将带到 neual network中得到一个
, neual network的希望得到值
就是最正确的,
定义和
之间的距离就是
,然后L对w偏微分
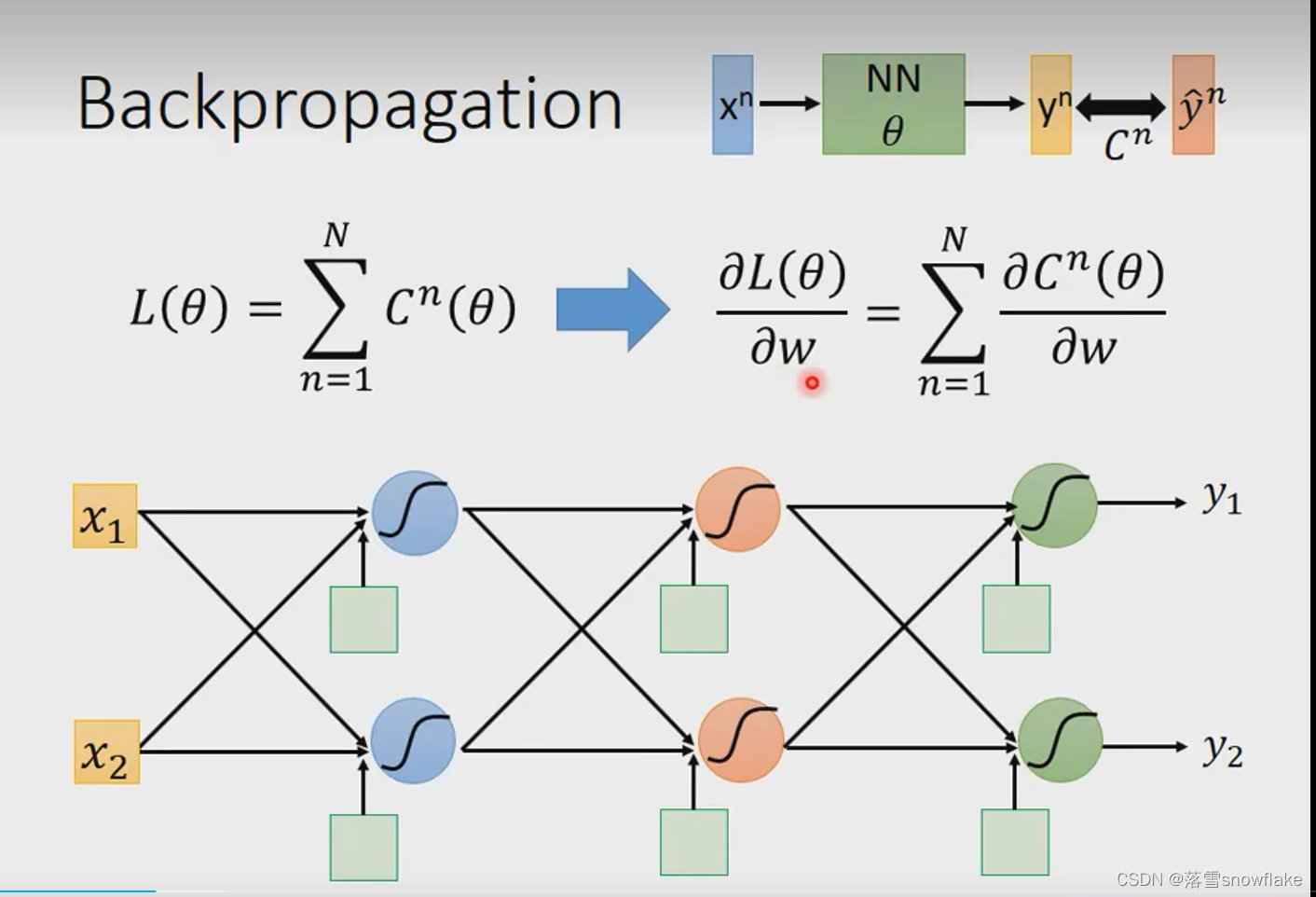
如何计算,先求每一个c对w偏微分,再求和。
先考虑某一个neual,
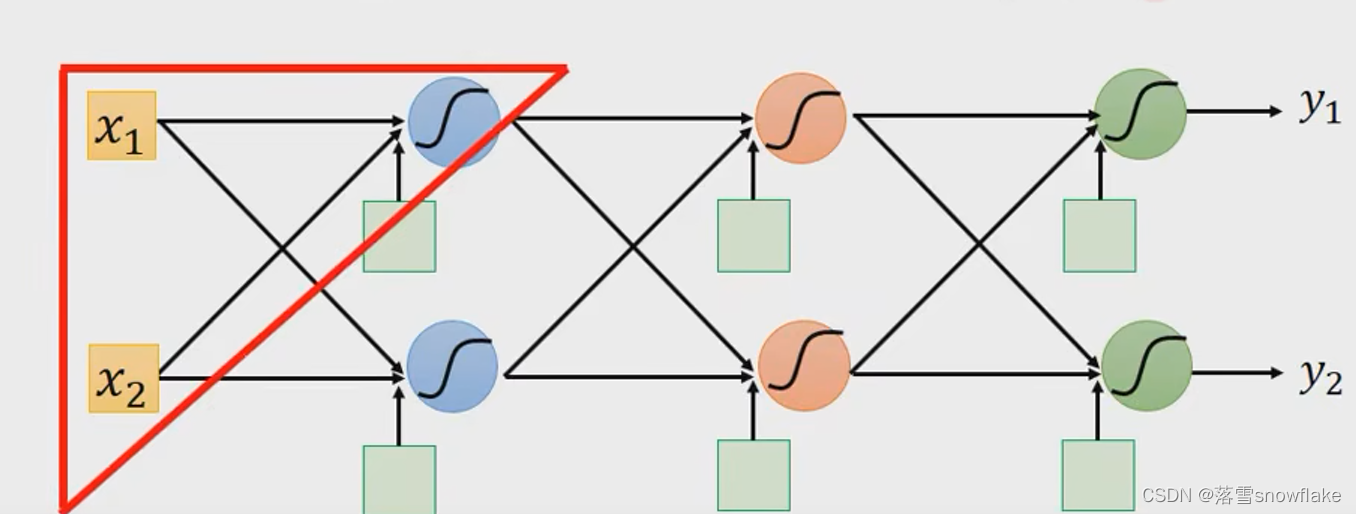
在计算损失函数函数的时候,总的损失函数可以写成每一个训练样本所构成的损失函数之和。而每一个样本所构成的损失函数为这个样本经模型输出后,模型的预测值与样本实际值之间的差距。不管是交叉熵还是均方误差都是在衡量这个差距。
那么为了分析总的损失函数,对总的损失函数求导,我们可以对每个样本的损失函数进行求导进行分析,之后进行求和分析就行了。先对上图中红色三角形的一个小的逻辑回归进行分析。
第一个layer的neual

拿w作为例子计算:计算,就是转化为求
.
Forward pass :计算
对一个逻辑回归进行分析,每个逻辑回归先进行一个线性的运算过程,在进行一个sigmoid函数处理过程,当然激活函数也是可以选择其他激活函数的。
那么对损失函数求导就可以拆成两项分布求导的积,如图,一项是损失函数对z求导(z为逻辑回归中的线性方程),一项是z对我们需要梯度下降的参数w的求导。
z对w求导称为前向传播,损失函数对z求导称为反向传播。

Backpropagation-Forward pass
先看如何计算,
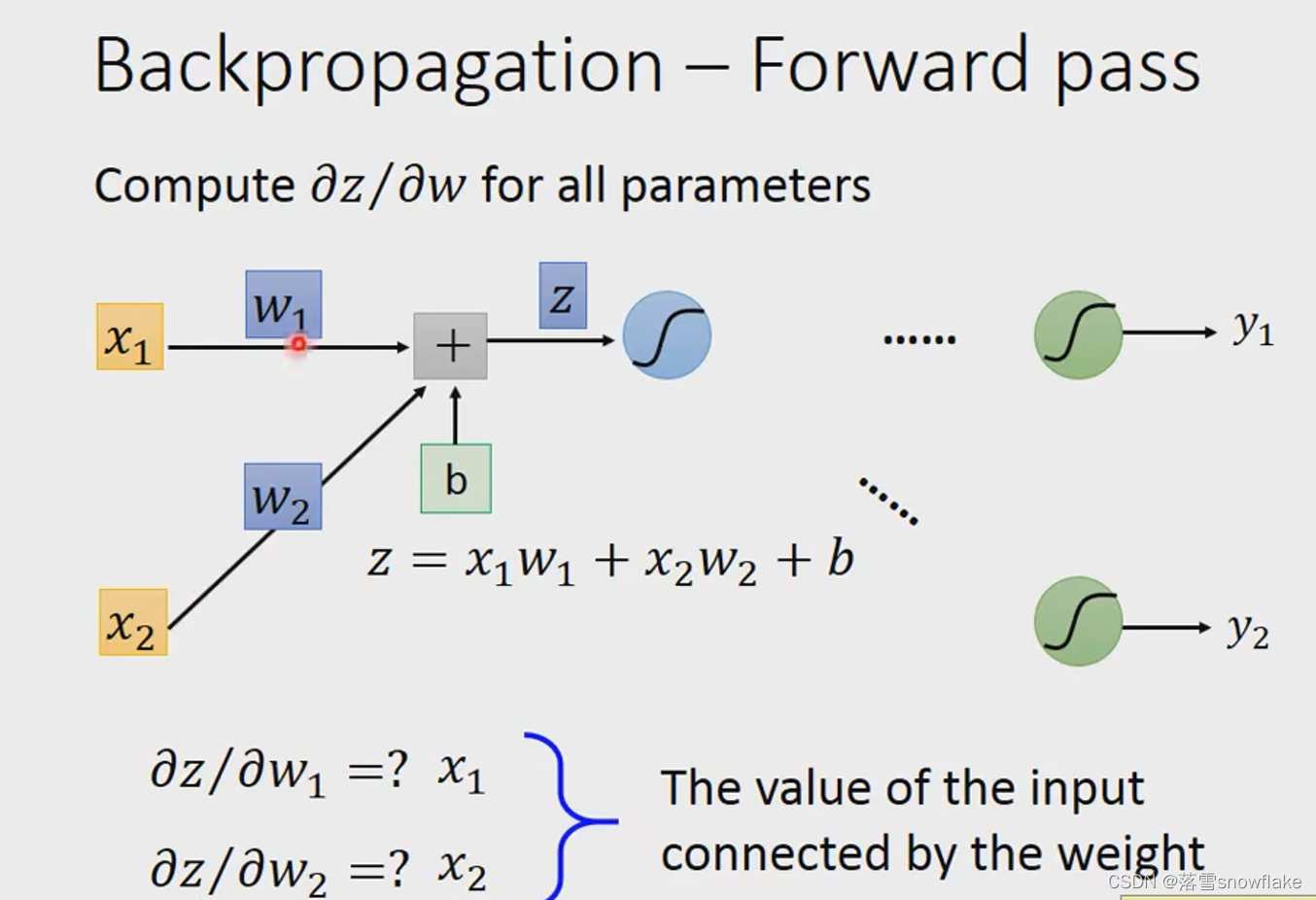
规律是看w前面接的是什么,w1再上图中接的是x1,w2接的是x2;也就是看它的input,input是什么偏微分就是什么。



最后得到的是:
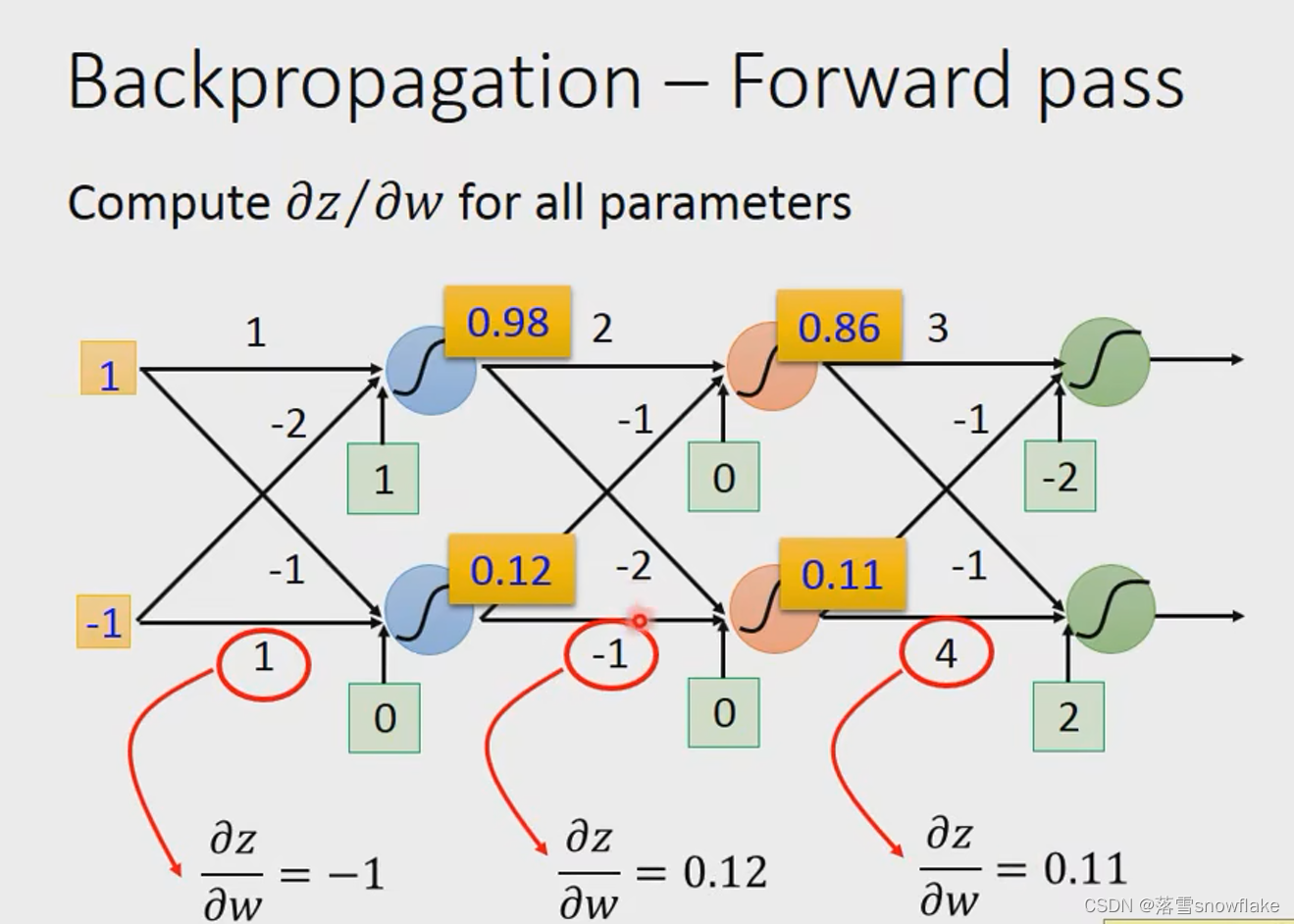
那么我们就能够很容易理解前向传播了,对于前向传播中的偏微分,这个值应该是上一级的输出值,这也代表了前向传播中某一个参数的权重。
Backpropagation-Backward pass
求,

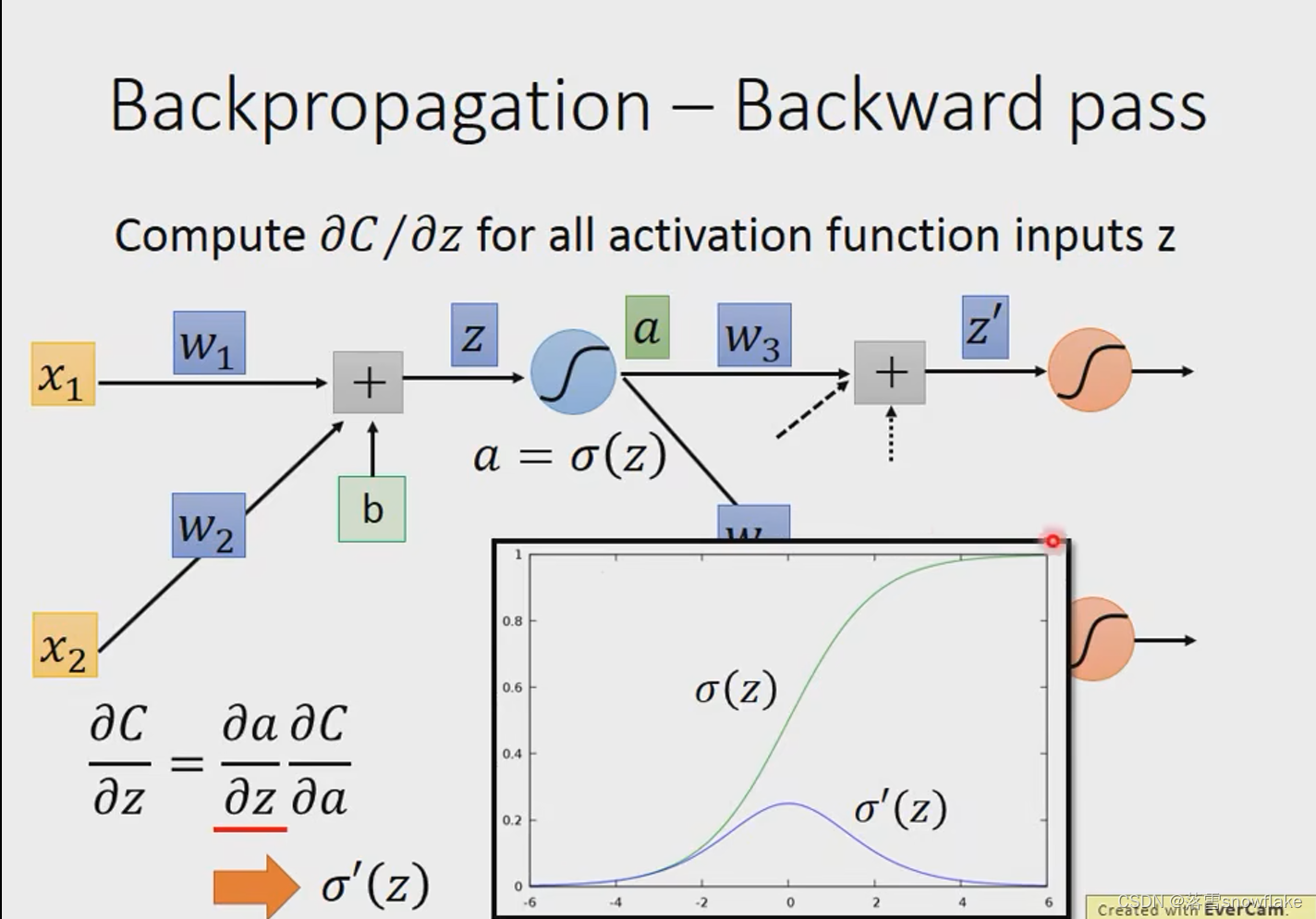
接下来对反向传播进行求解分析,如上图。从这一节神经元向之后的神经元看过去,对z需要进行一个激活函数的运算(这个例子假设是sigmoid函数),后作为下一级的输入。那我们的反向传播的偏微分就可以写成图中的相乘的形式,由损失函数对激活函数偏导乘激活函数对z偏导。


那么另一部分怎么求解呢?假设我们这个模型是下一级只连接了两个神经元(更多神经元如果理解这个后也就明白了),那么我们的输出结果就会对之后的两个神经元产生影响,那么我们可以用求导的链式法则去表示出上一步我们需要求解的部分,如上图。我们发现图中的两个部分还是没有求解出来。
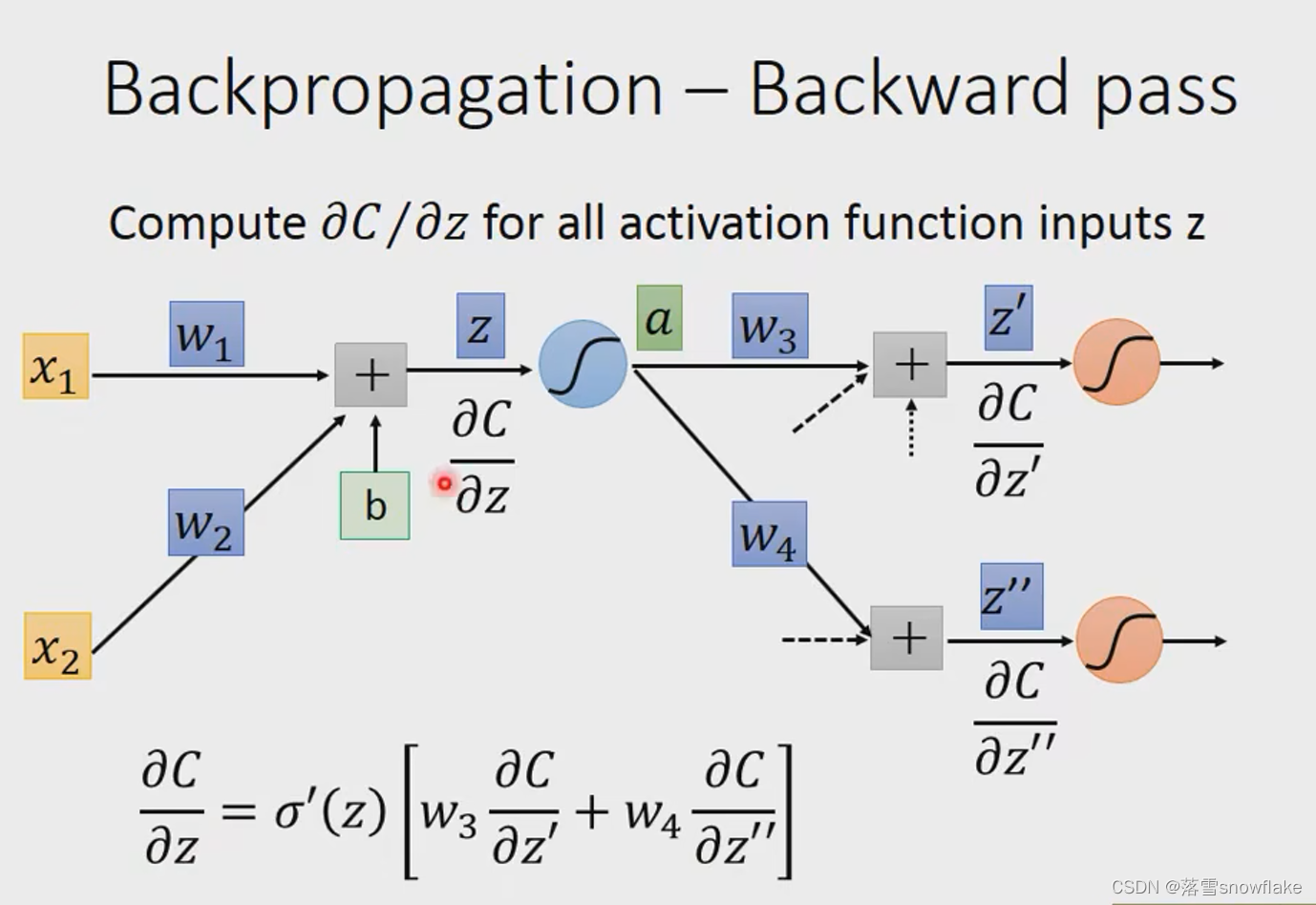
另外一个neural,

换一种思路去更好的理解反向传播,如上图。可以看成是一个新的网络,这个网络是和我们刚才的网络输入输出是相反的。这个网络输入了下图中的偏导数,经过上文中介绍的处理方式,得到了之前一级的偏导数,这就是一种反向传播。
而对于σ(z)函数的偏导,z在输入的时候就已经确定了具体的大小,所以σ(z)函数的偏导也就是确定的常数了
最终计算下图中的红方块值


如上图,当下一层为输出层的时候,由于我们在输入样本时是可以计算出输出值y1和y2,所以这部分的偏导数也是可以很容易做出来的。

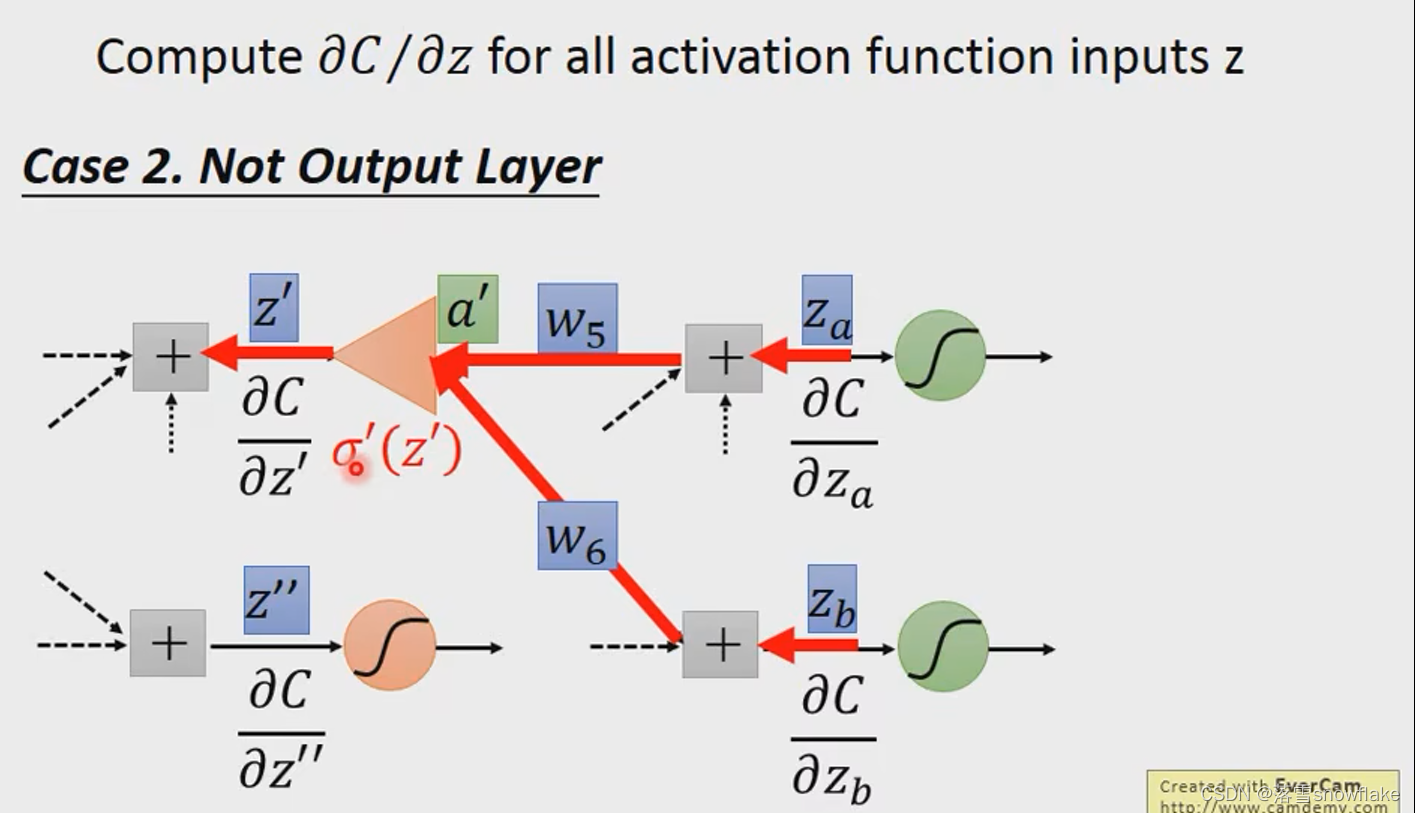

这种情况下,我们很容易想到,如果知道下一层的微分值,那么不是可以很容易求解出这一层的微分值嘛?
这时大家肯定想到了递归的思想,不断的递归就可以推到输出层从而计算出我们想要的结果。
一直推到outputlayer。
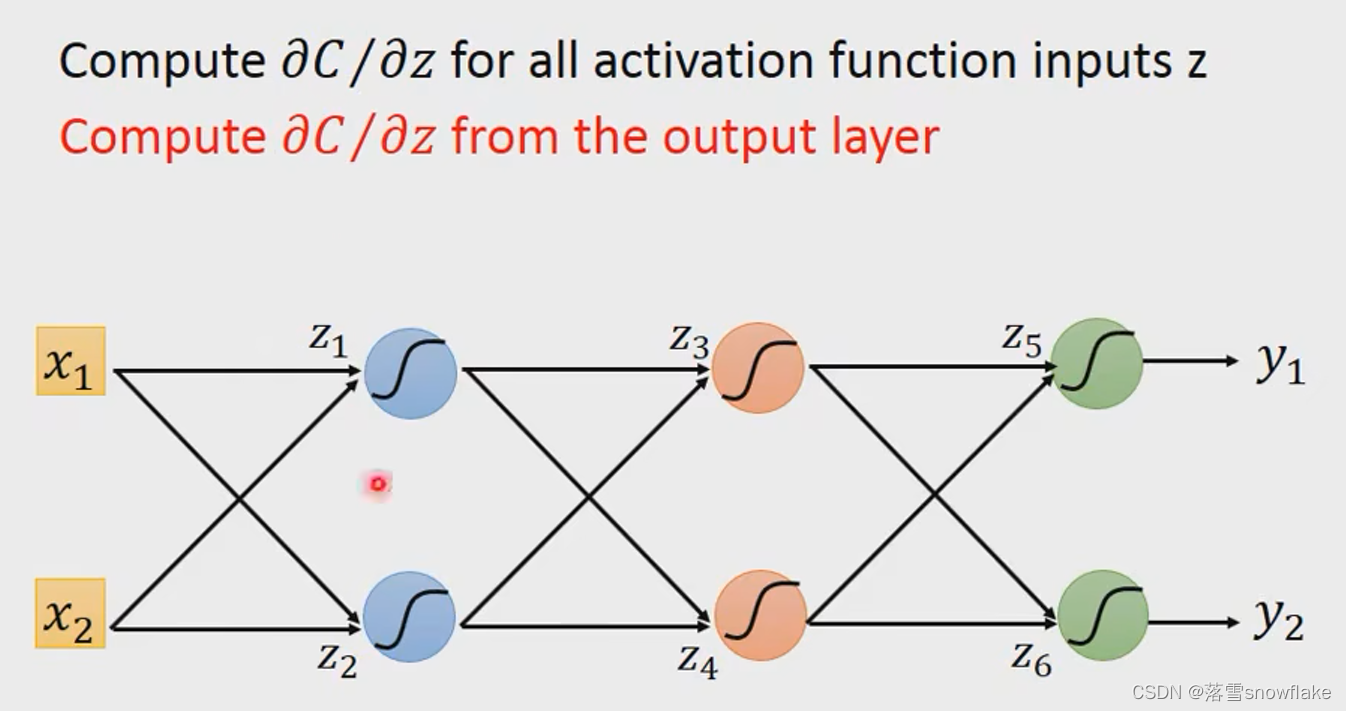

从后往前比从前往后更加有效率
建立一个新的反向的neual work运算
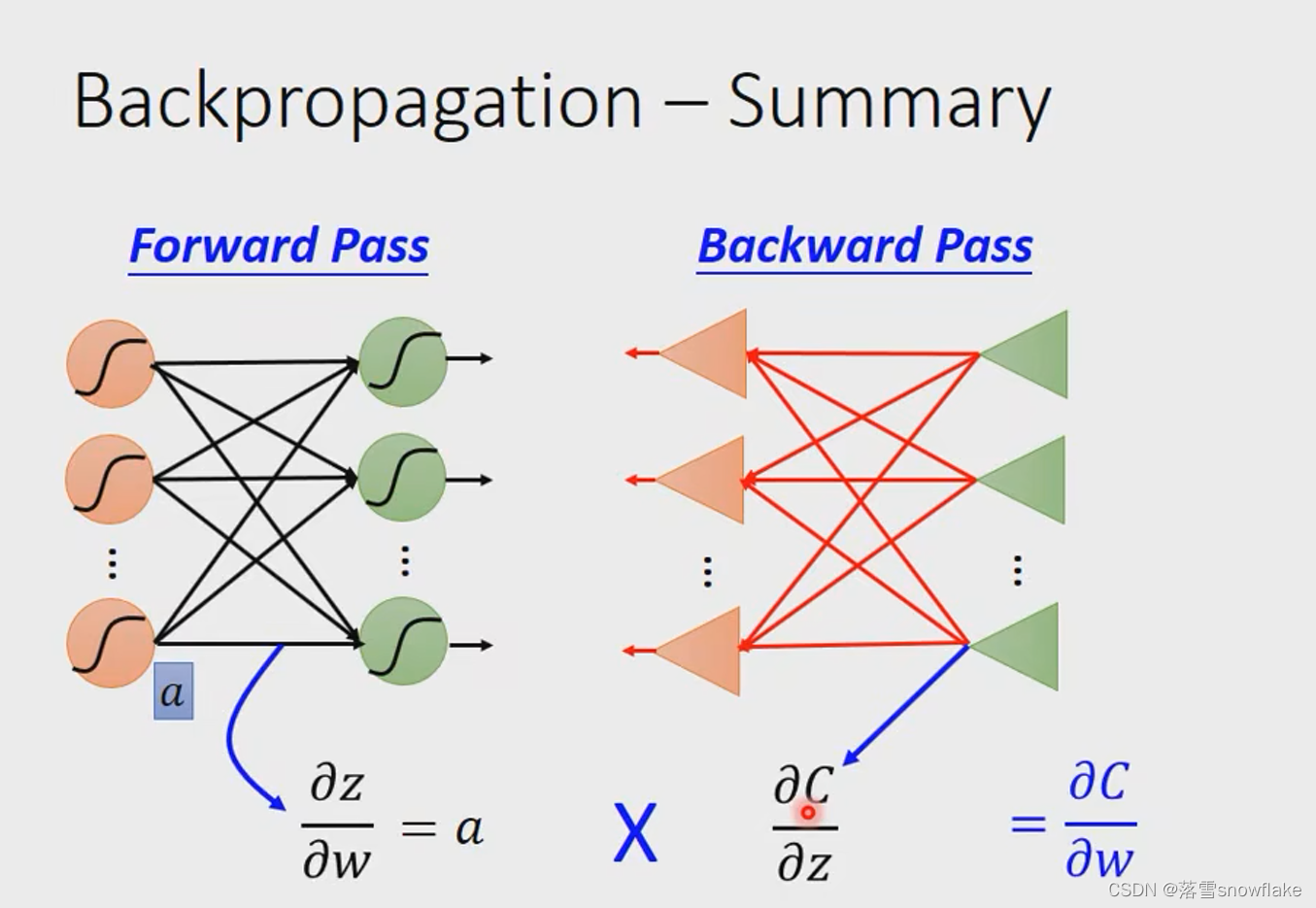
最后在这个部分总结下bp,bp是为了简化对神经网络做梯度下降时带来的运算量巨大的问题。bp主要分为反向传播和前向传播。
前向传播很容易,主要传播的就是神经网络的输入。这个每一级的输入都会作为我们的偏导数来供我们去做梯度下降。
反向传播传播的是损失函数对z的偏导(z是每一级线性方程的输出),这个偏导数可以通过,从输出层到输入层的反向求解,使得运算达到进一步的简化。