125 · 背包问题（二）LintCode 炼码

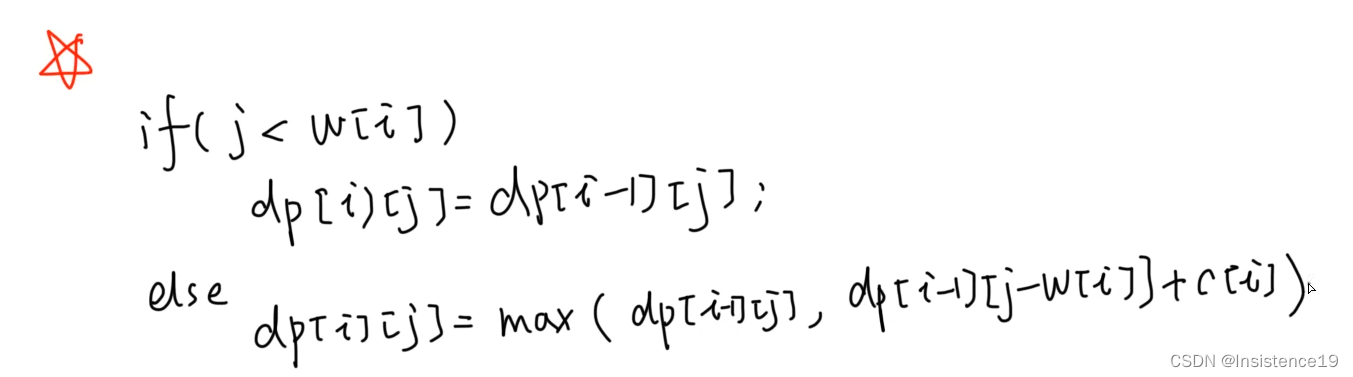
class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param a: Given n items with size A[i]
     * @param v: Given n items with value V[i]
     * @return: The maximum value
     */
    int backPackII(int m, vector<int> &a, vector<int> &v) {
        // write your code here
        int n = a.size();
        vector<vector<int>> dp(n+1, vector<int> (m+1, 0));
        for(int i = 1; i <= n; ++i)
        {
            for(int j = 1; j <= m; ++j)
            {
                if(j<a[i-1])
                {
                    dp[i][j] = dp[i-1][j];
                }
                else
                {
                    dp[i][j] = max(dp[i-1][j], dp[i-1][j-a[i-1]]+v[i-1]);
                }
            }
        }
        return dp[n][m];
    }
};

0-1背包滚动数组优化

滚动数组思想（后无效性原则）

滚动数组是DP中的一种编程思想。简单的理解就是让数组滚动起来,每次都使用固定的几个存储空间,来达到压缩,节省存储空间的作用。起到优化空间,主要应用在递推或动态规划中(如01背包问题)。因为DP题目是一个自底向上的扩展过程,我们常常需要用到的是连续的解,前面的解往往可以舍去。

注意:背包剩余容量需要从最大值开始推不然物品的小容量值会被这个物品的小容量值覆盖

将二维数组利用滚动数组思想转入一维数组，每次都对一个一维数组进行操作，这里注意的是需要每次从数组的最后一个元素开始处理，因为如果从左往右就会出现后面元素利用本次处理后的结果，我们应该是希望对上一轮循环的结果进行重新处理，而不是使用本轮循环所更改的元素。

class Solution {
public:
    int backPackII(int m, vector<int> &a, vector<int> &v) {
        // write your code here
        int n = a.size();
        vector<int> dp(m+1, 0);
        for(int i = 1; i <= n; ++i)
        {
            // 为了防止数据被覆盖每次从最后一个元素开始算起
            for(int j = m; j >= 0; --j)
            {
                if(j>=a[i-1])
                {
                    dp[j] = max(dp[j], dp[j-a[i-1]]+v[i-1]);
                }
            }
        }
        return dp[m];
    }
};

0-1背包问题（一）LintCode 炼码

【解法一】二维数组

class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param a: Given n items with size A[i]
     * @return: The maximum size
     */
    int backPack(int m, vector<int> &a) {
        // write your code here
        int n = a.size();
        vector<vector<int>> dp(n+1, vector<int> (m+1, 0));
        for(int i = 1; i <= n; ++i)
        {
            for(int j = 1; j <=m; j++)
            {
                if(j<a[i-1])
                {
                    dp[i][j] = dp[i-1][j];
                }
                else
                {
                    dp[i][j] = max(dp[i-1][j], dp[i-1][j-a[i-1]]+a[i-1]);
                }
            }
        }
        return dp[n][m];
    }
};

【解法二】滚动数组

class Solution {
public:
    int backPack(int m, vector<int> &a) {
        // write your code here
        int n = a.size();
        vector<int> dp(m+1, 0);
        for(int i=1; i<=n; ++i)
            for(int j=m; j>=1; j--)
                if(j>=a[i-1])
                dp[j] = max(dp[j], dp[j-a[i-1]]+a[i-1]);
        return dp[m];
    }
};

#include<iostream>
using namespace std;
#include<vector>
int dp[35][205];
int w[35], c[35];

class Solution {
public:
    /**
     * @param m: An integer m denotes the size of a backpack
     * @param a: Given n items with size A[i]
     * @param v: Given n items with value V[i]
     * @return: The maximum value
     */
    int backPackII(int m, vector<int>& a, vector<int>& v) {
        // write your code here
        int n = a.size();
        vector<int> dp(m + 1, 0);
        for (int i = 1; i <= n; ++i)
        {
            for (int j = m; j >= 0; j--)
            {
                if (j >= a[i - 1])
                {
                    dp[j] = max(dp[j], dp[j - a[i - 1]] + v[i - 1]);
                }
            }
            for (int k = 1; k <= m; k++)
                cout << dp[k] << " ";
            cout << endl;
        }
        return dp[m];
    }
};