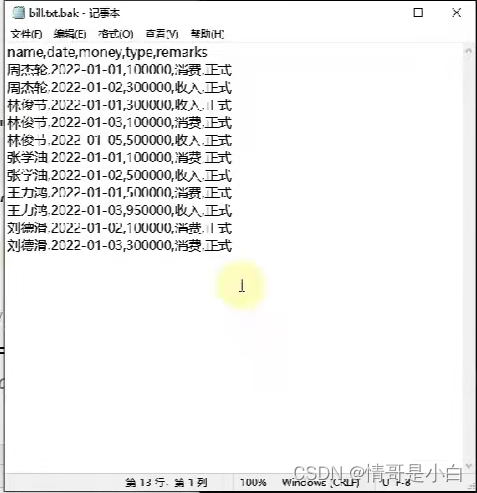
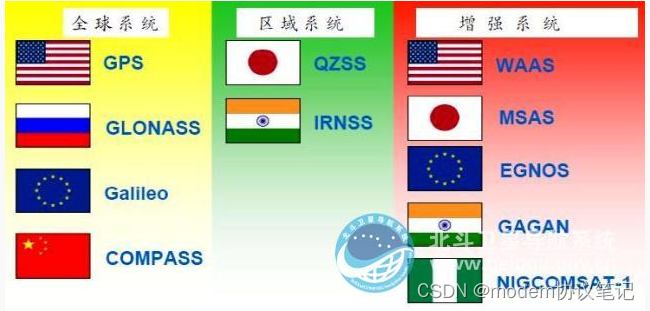
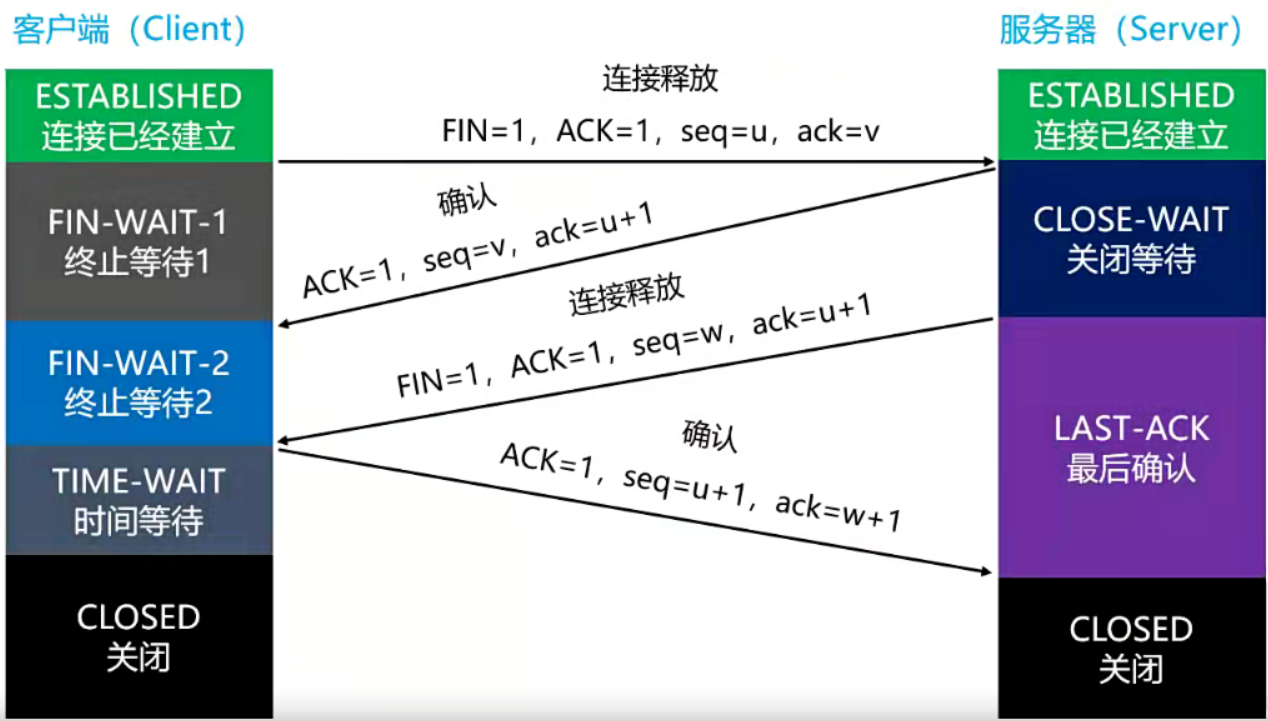
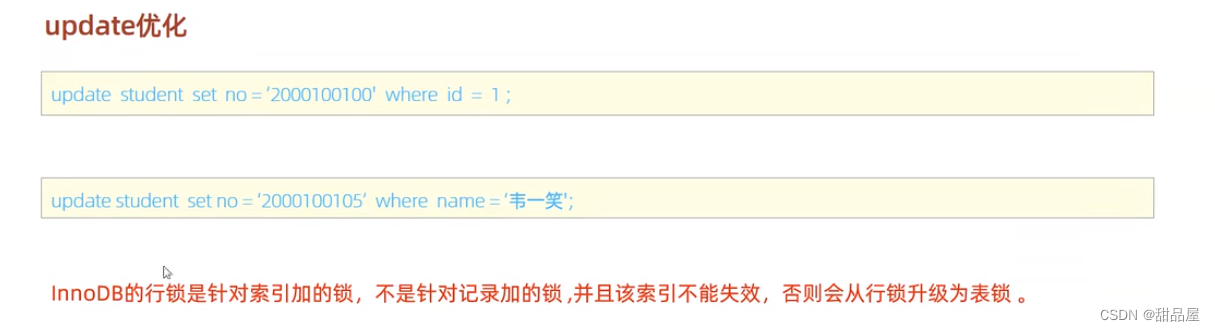
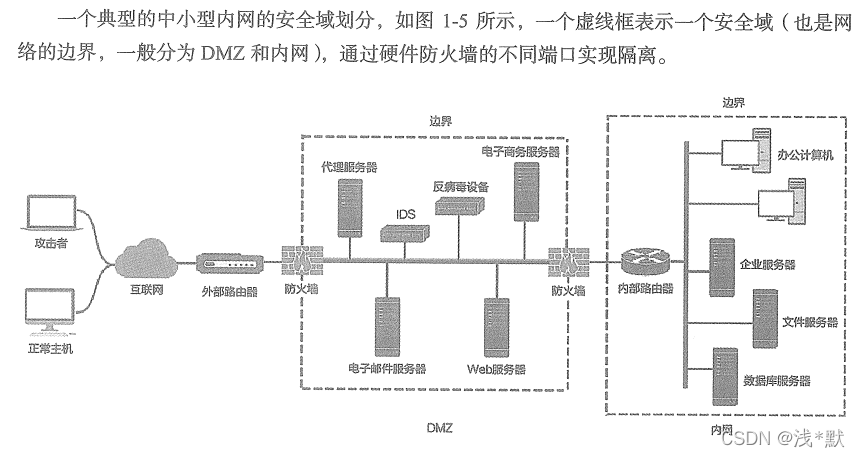
文章目录
- 例题
- 1. 804.n的阶乘
- 2. 805.x和y的最大值
- 3. 808.最大公约数
- 4. 811.交换数值
- 5. 812.打印数字
- 6. 813.打印矩阵
- 7. 819.递归求阶乘
- 8. 820.递归求斐波那契数列
例题
1. 804.n的阶乘
Acwing 804.n的阶乘
#include<iostream>
using namespace std;
int fact(int n)
{
if(n == 1) return 1;
return n * fact(n - 1);
}
int main()
{
int n;
cin >> n;
cout << fact(n) <<endl;
return 0;
}
2. 805.x和y的最大值
Acwing 805.x和y的最大值
#include<iostream>
using namespace std;
int max(int x,int y)
{
return x>y?x:y;
}
int main()
{
int n, m;
cin >> n >> m;
cout << max(n,m) << endl;
return 0;
}
3. 808.最大公约数
Acwing 808.最大公约数
#include<iostream>
using namespace std;
int gcd(int a, int b)
{
for(int i = 1000; i > 0; i--)// 直接进行计算
if(a % i == 0 && b % i == 0)
return i;
return 0;
}
int main()
{
int n, m;
cin >> n >> m;
cout << gcd(n, m) << endl;
return 0;
}
4. 811.交换数值
Acwing 811.交换数值
#include<iostream>
using namespace std;
void swap(int &x, int &y)
{
int t = x;
x = y;
y = t;
}
int main()
{
int n, m;
cin >>n >> m;
swap(n, m);
cout << n << ' '<< m << endl;
return 0;
}
5. 812.打印数字
Acwing 812.打印数字
#include<iostream>
using namespace std;
const int N = 1010;
int a[N];
void print(int a[], int size)
{
for(int i = 0; i < size;i ++)
cout << a[i] << ' ';
cout << endl;
}
int main()
{
int n, size;
cin >> n >> size;
for(int i = 0; i < n; i++) cin >> a[i];
print(a,size);// 这里直接写数组名就可以
return 0;
}
6. 813.打印矩阵
Acwing 813.打印矩阵
#include<iostream>
using namespace std;
void print2D(int a[][100], int row, int col)
{
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
cout << a[i][j] << ' ';
}
cout << endl;
}
}
int main()
{
int row, col;
cin >> row >> col;
int a[100][100];
for(int i = 0; i < row; i++)
for(int j = 0; j < col; j++)
cin >> a[i][j];
print2D(a, row, col);
return 0;
}
7. 819.递归求阶乘
Acwing 819.递归求阶乘
#include<iostream>
using namespace std;
int fact(int n)
{
if(n == 1) return 1;
else return n * fact(n - 1);
}
int main()
{
int n;
cin >> n;
cout << fact(n) << endl;
return 0;
}
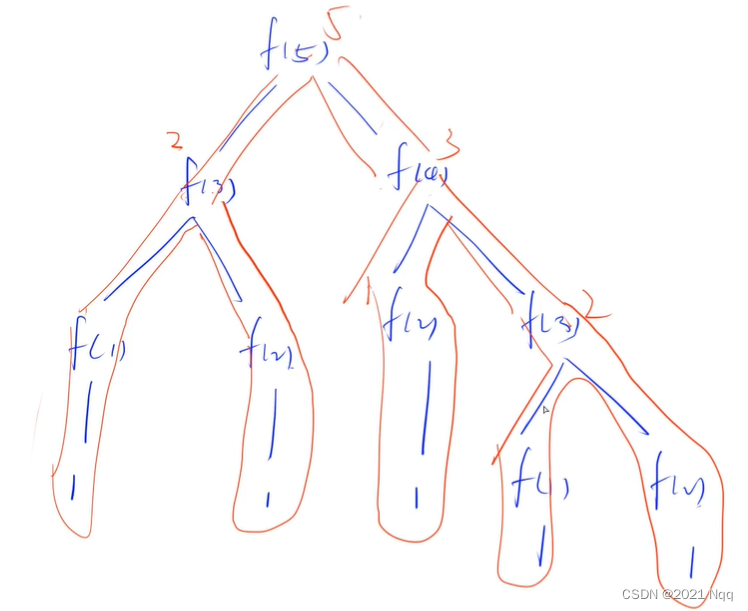
8. 820.递归求斐波那契数列
Acwing 820 .递归求斐波那契数列
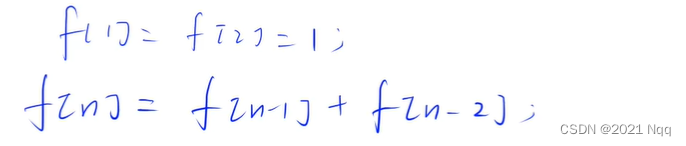
- 树的深度优先遍历
#include<iostream>
using namespace std;
int f(int n)
{
if(n <= 2) return 1;
return f(n - 1) + f(n - 2);
}
int main()
{
int n;
cin >> n;
cout << f(n) << endl;
return 0;
}