文章目录
- 前言
- 非参数检验
- 两个独立样本的Mann-Whitney检验
- 练习
前言
本片是对非参数检验最后的介绍。
非参数检验
两个独立样本的Mann-Whitney检验
Mann -Whitney检验也称为Mann- Whitney U检验(Mann-Whitney U test)或称为 Wilcoxon秩和检验,它是由 Henry B.Mann和D.R. Whitney于1947年提出的。用于确定两个总体间是否存在差异的一种非参数检验方法,该检验是两个独立样本t检验(或者z检验)的一种替代方法(参数方法),但它不需要诸如总体服从正态分布且方差相等之类的假设,唯一的要求是两个独立随机样本的数据至少是顺序数据。
Mann -Whitney检验与Wilcoxon符号秩检验不同,它不基于相关样本,而是使用两个独立样本。

H0 :两个总体相同,H1 :两个总体不相同
或等价于
H0:Mx=My ;H1:Mx≠My
当Mann -Whitney检验拒绝H0时,可以得出两个总体不同的结论,但并不能证实它们究竟在哪些方面
是不同的,两个总体可能有不同的均值、不同的方差,或者不同的分布形式。
Mann -Whitney-检验也可以用于判断两个总体在中心位置上是否相同,也就是考察总体X的中位数
和总体Y的中位数 是否相等,因此也可提出如下形式的假设
H0:Mx=My ;H1:Mx≠My
H0:Mx=My ;H1:Mx≠My
如果H0为真,那么将m个x和n个y的数据混合在一起,并从小到大排列,这m+n=N个数据能够看作来
自相同总体的一个随机样本.若大部分的x大于y,或大部分的y大于x,则不能证明这n+m=N个数据来
自同一个总体,因此应拒绝H0
检验步骤
把两组数据混合在一起,得到m+n=N个数据,将N个数据从小到大排列,并找出N个数据的秩。
分别对样本(x1,x2,…,xm)和(y1,y2,…,yn)的秩求出平均秩,得到两个平均秩 和 ,并对平均秩的差距进行比较:若二者相差甚远,意味着一组样本的秩普遍偏小,另一组样本的秩普遍偏大,此时原假设有可能不成立,计算样本(x1,x2,…,xm)中每个秩大于样本(y1,y2,…,yn)的每个秩的个数 ,以及样本(y1,y2,…,yn)中每个秩大于样本(x1,x2,…,xm)中每个秩的个数,并对 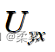 和
和 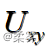 进行比较,如果相差较大,此时原假设有可能不成立。
进行比较,如果相差较大,此时原假设有可能不成立。

例题:
(数据: example6_6. RData)沿用例6-6。假定不知道两家企业生产的灯泡的使用寿命服从何种分布,检验两家企业生产的灯泡的使用寿命是否相同( 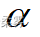 =0.05)
=0.05)
解:将甲企业作为一个总体X,乙企业作为另一个总体Y,要检验两家企业生产的灯泡的使用寿命是否相同,就是检验两个总体的位置参数是否相等。因此提出如下假设:
H0:M甲=M乙;H1:M甲≠M乙
首先将两组数据混合在一起,得到20+20=40个数据,将40个数据从小到大排列,并找出它们的秩。然后计算检验统计量,并根据P值做出决策。检验的R代码和结果如下所示
函数wilcox.test(x,y,)中的x和y是两个样本。 paired=true表示进行配对检验,默认 paired=FALSE。
load("C:/example/ch6/example6_6.RData")
attach(example6_6)
wilcox.test(甲企业,乙企业)
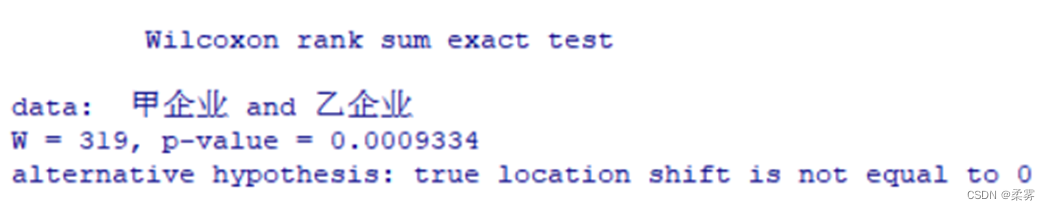
结论:在该项检验中,统计量W=319,P=0.009334,P<0.05,拒绝H0,有证据显示两家企业灯泡的使用寿命有显著差异。
注:函数wilcox.test(x,y,)中的x和y是两个样本。 paired=true表示进行配对检验,默认 paired=FALSE。
Wilcoxon符号秩检验是配对样本t检验(参数方法)的一种替代方法,该检验只要
求两个样本的数据之差服从对称分布。
检验两个总体的分布是否相同,或者说两个总体的中位数是否相同
设X,Y是两个连续的总体,且具有对称分布,两个总体分别随机抽取n个观察值,
组成n个数对(x1,y1),(x2,y2),…(xn,yn),每个数对的差记为di=xi-yi
若X,Y是具有相同分布的总体,则有P(di>0)=P(di<0),即xi>yi的概率与xi<yi
的概率相等,这也意味着差值di的中位数等于0。用Md表示差值di的中位数,如果关
心两个总体的分布是否相同,或者说两个总体的中位数是否相同,可以建立如下假
设: H0: Md=0 ;H1: Md≠0 (Md表示差值的中位数)
检验步骤
计算各数据对的差值di,并取绝对值,排序后求出秩,最小的|di|秩为1,最大的|di|秩为n。如果有相同的|di|则取各点秩的均值 。
计算检验统计量W或z:
对于正的di的秩和负的di的秩分别加总,得到正秩的总和 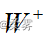 与负秩的总和
与负秩的总和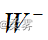 Wilcoxon符号秩检验的统计量是
Wilcoxon符号秩检验的统计量是 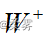 和
和 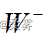 中的较小者。对于双侧检验H0: Md=0 ;H1: Md≠0;在H0为真时
中的较小者。对于双侧检验H0: Md=0 ;H1: Md≠0;在H0为真时 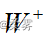 与
与 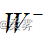 的大小应该近似相等,如果二者差异较大应怀疑H0,根据P值作出决策。
的大小应该近似相等,如果二者差异较大应怀疑H0,根据P值作出决策。

例题:
(数据: example6_7. RData)沿用例6-7。检验消费者对两种饮料的评分是否有显著差异( =0.05)
解:设消费者对新款饮料的评分为X,对旧款饮料的评分为Y
提出如下假设:
H0:X=Y;H1:X≠Y
load("C:/example/ch6/example6_7.RData")
attach(example6_7)
wilcox.test(旧款饮料,新款饮料,paired=TRUE)

结论:在该项检验中,在该项检验中,V=5.5,P=0.04759,P<0.05,拒绝H0,有证据显示消费者对新旧饮料的评分有显著差异。
练习
1、(exercise6_9.RData)为了解一种节能灯的使用寿命,随机抽取了10只灯泡,测得其使用寿命(单位:小时)如exercise6_9.RData所示,采用 Wilcoxon符号秩检验检验该种节能灯使用寿命的中位数是否等于6000小时(α=0.05)。
设:M1代表该种节能灯使用寿命的中位数;M2 代表该种节能灯使用寿命的中位数为6000
H0:M1=M2 H1:M1 ≠M2
wilcox.test(exercise6_9$寿命,m=6000)
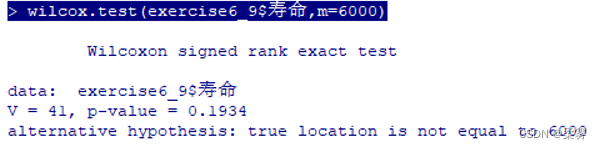
结论:在该项检验中,V=41,P=0.1934,P>0.05,不拒绝H0,故有证据表明该种节能灯使用寿命的中位数为6000小时。
2、(exercise6_10.RData)某种品牌的彩电在两个城市销售,在A城市和B城市各有8个商场销售。exercise6_10.RData记载了各商场一年的销售量(单位:台)。采用Mann- Whitney检验分析两个城市的销售量是否有显著差异(α=0.05)。
设:设:μ1为A城市一年销售量的中位数;μ2为A城市一年销售量的中位数
H0:μ1=μ2 H1:μ1 ≠μ2
attach(exercise6_10)
wilcox.test(A城市,B城市)

结论:在该项检验中,V=26.5,P=0.5992,P>0.05,不拒绝H0,故有证据表明两个城市的销售量有显著差异。
3、(exercise6_11.RData)为分析股票的每股盈利状况,在某证券市场上随机抽取10只股票,得到上年度和本年度的每股盈利(单位:元)数据如exercise6_11.RData所示。采用 Wilcoxon符号秩检验分析:本年度与上年度相比,每股盈利是否有显著提高(α=0.05)。
设Md为上年度每股盈利的中位数与本年度每股盈利的中位数的差值。
H0:Md>=0 H1:Md < 0
wilcox.test(exercise6_11$上年度,exercise6_11$本年度,alt=”less”,paired=T)
结论:在该项检验中,P= 0.04147,P<0.05,拒绝原假设,有证据表明,本年度与上年度相比,每股盈利有显著提高。