两种实现方式
循环式
一般对于一维的DP问题可以应用。
for(len = 1; len <= n; len++)
for(l = 1; l + len-1 <= n; l++)
r = l + len - 1;
//枚举方案数
记忆化搜索式
一般在二维DP中使用
循环也倒是可以,但是层数太多,所以使用记忆化进行实现。
常见策略
环形变链
原理:
- 对于一个环形的DP,(例如石子合并),每合并一次,就相当于在石子之间连了一条边。总共需要 n − 1 n-1 n−1次合并,所以还有一条边没有连。所以理所应当可以在缺口处断开。
- 由于有n个缺口,所以要枚举缺口的位置(时间复杂度 O ( N 4 ) O(N^4) O(N4)),不可行
- 但是如果把原来的链复制一份,拼在后面,这样的话,做一次DP,就可以得到从所有缺口处断开的值,时间复杂度 O ( ( 2 N ) 3 ) O( \space (2N)^3 \space ) O( (2N)3 )
1068. 环形石子合并
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入样例:
4
4 5 9 4
输出样例:
43
54
#include <bits/stdc++.h>
using namespace std;
#define N 402
int a[N];
int s[N];
int f[N][N];
int g[N][N];
int n;
int main()
{
scanf("%d", &n);
for(int i =1; i <= n; i++)
{
scanf("%d", a+i);
a[i+n] = a[i];
}
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= 2 *n; i++) f[i][i] = 0;
for(int i = 1; i <= 2 * n; i ++){
s[i] = s[i - 1] + a[i];
}
for(int len = 1; len <= n; len ++){
for(int l = 1; l + len - 1 <= 2 * n; l++){
int r = l + len - 1;
for(int k = l; k < r; k++){
f[l][r] = min(f[l][r], f[l][k] + f[k+1][r] + s[r] - s[l - 1]);
g[l][r] = max(g[l][r], g[l][k] + g[k+1][r] + s[r] - s[l - 1]);
}
}
}
int maxv = 0, minv = 0x3f3f3f3f;
for(int i = 1; i <= n; i++){
maxv = max(maxv, g[i][i + n - 1]);
minv = min(minv, f[i][i + n - 1]);
}
printf("%d\n%d", minv, maxv);
return 0;
}
320. 能量项链
在Mars星球上,每个Mars人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是Mars人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为m,尾标记为r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 mrn(Mars单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设N=4,4颗珠子的头标记与尾标记依次为(2,3) (3,5) (5,10) (10,2)。
我们用记号⊕表示两颗珠子的聚合操作,(j⊕k)表示第 j,k 两颗珠子聚合后所释放的能量。则
第4、1两颗珠子聚合后释放的能量为:(4⊕1)=1023=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为((4⊕1)⊕2)⊕3)= 1023+1035+10510=710。
输入格式
输入的第一行是一个正整数 N,表示项链上珠子的个数。
第二行是N个用空格隔开的正整数,所有的数均不超过1000,第 i 个数为第 i 颗珠子的头标记,当i<N时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第1颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
输入样例
4
2 3 5 10
输出样例
710
其实就是类似于算法书上的矩阵连乘的优化。
#include <bits/stdc++.h>
using namespace std;
#define N 204
int a[N];
int f[N][N];
int n;
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", a+i);
a[i+n] = a[i];
}
a[1+2*n] = a[1];
for(int len = 2; len <= n; len++)
{
for(int l = 1; l + len - 1 <= n * 2; l++){
int r = l + len - 1;
for(int k = l; k <r; k++){
f[l][r] = max(f[l][r], f[l][k] + f[k+1][r] + a[l]*a[k+1]*a[r+1]);
}
}
}
int maxv = 0;
for(int i = 1; i<= n; i++){
maxv = max(maxv, f[i][i + n - 1]);
}
printf("%d", maxv);
return 0;
}
1069. 凸多边形的划分
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 N,表示顶点数量。
第二行包含 N 个整数,依次为顶点 1 至顶点 N 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N≤50
数据保证所有顶点的权值都小于
1
0
9
10^9
109
输入样例:
5
121 122 123 245 231
输出样例:
12214884
这一道题目根本不需要当成环,然后拆开来复制一份!!!
相关基本原理
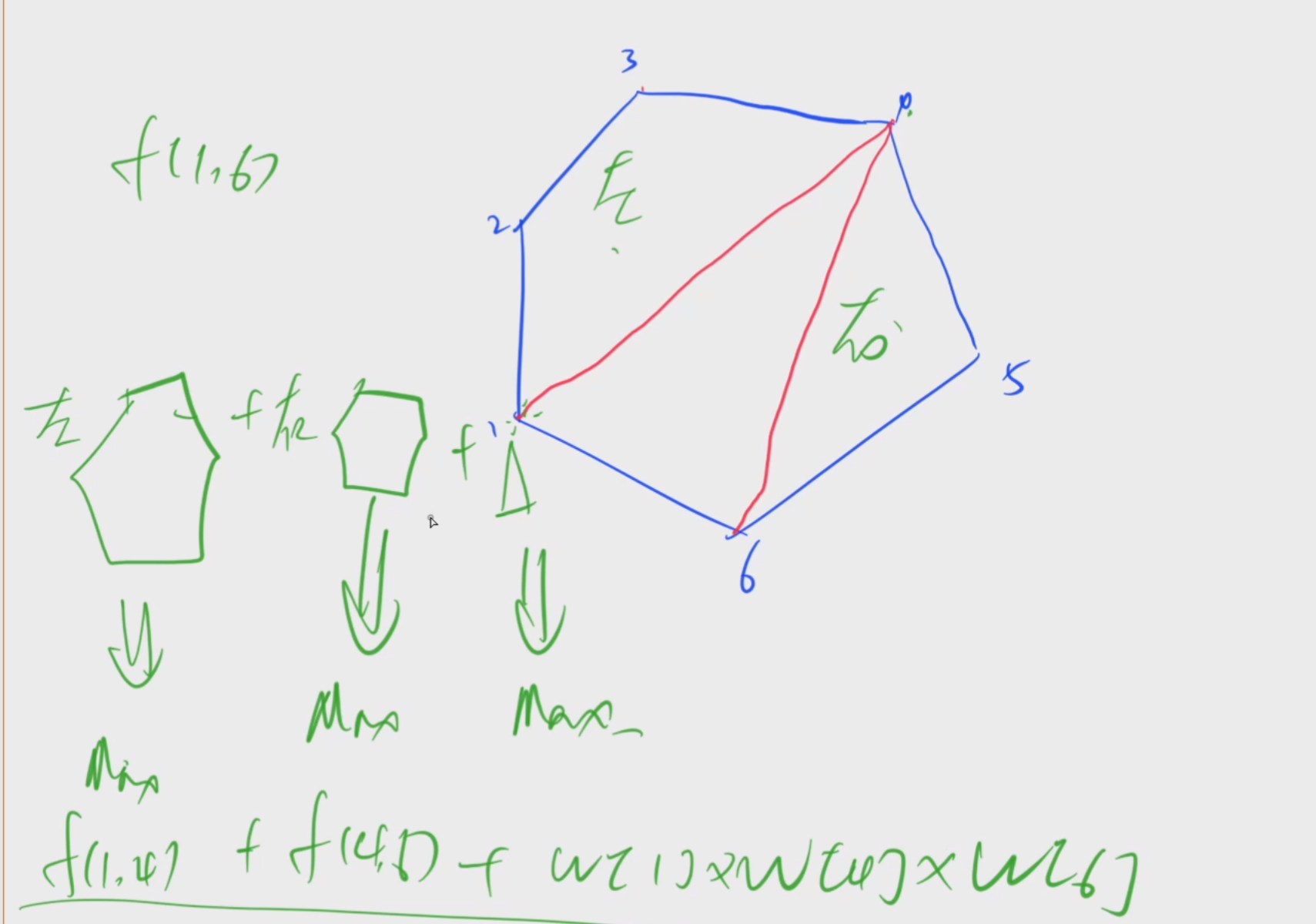
- 要是把这一个多边形剖分以后,每一个外面的边都是一个三角形的边。所以我随便取一条边开始。
- 通过这条边,取异于这一条边的两个端点的中间的点,连起来,就是一个三角形。
- 这个三角形,把原来的分成了两部分,一部分是左面,一部分是右面,还有一部分是中间的三角形。
首先,据说java还有高精度,所以我先尝个鲜
import java.util.Scanner;
import java.math.BigInteger;
public class Main {
static final int N = 55;
static BigInteger f[][] = new BigInteger[N][N];
static int n;
static int []w = new int[N];
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
n = scan.nextInt();
for(int i = 1; i <= n; i++) w[i] = scan.nextInt();
for(int i = 0; i <= n; i++) {
for(int j = 0; j <= n; j++) {
f[i][j] = BigInteger.valueOf(0);
}
}
for(int len = 3; len <= n; len ++) {
for(int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
f[l][r] = f[l][l+1].add(f[l+1][r]).add(BigInteger.valueOf(w[l]).multiply(BigInteger.valueOf(w[l+1])).multiply(BigInteger.valueOf(w[r])) );
for(int k = l + 2; k < r; k++) {
BigInteger tmp1 = f[l][k].add(f[k][r]);
BigInteger tmp2 = tmp1.add(BigInteger.valueOf(w[l]).multiply(BigInteger.valueOf(w[k])).multiply(BigInteger.valueOf(w[r])));
if(f[l][r].compareTo(tmp2) == 1) f[l][r] = tmp2;
}
}
}
System.out.println(f[1][n]);
}
}
java这么繁琐,快把老夫累死,还不如C++手搓高精度
手搓办法:首先假装不是高精度,然后再认为是高精度(这样成功率高一点)
第一步:先把样例过了
#include <bits/stdc++.h>
using namespace std;
#define N 55
typedef long long ll;
ll a[N];
long long f[N][N];
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%lld", a+i);
for(int len = 3; len <= n; len ++)
{
for(int i = 1; i + len - 1 <= n; i++){
int j = i + len - 1;
f[i][j] = 0x3f3f3f3f;
for(int k = i + 1; k < j; k++){
f[i][j] = min(f[i][j], f[i][k] + f[k][j] + a[i]*a[j]*a[k]);
}
}
}
cout << f[1][n];
return 0;
}
第二步:使用数组造一个高精度
第三步:最终代码
#include <bits/stdc++.h>
using namespace std;
#define N 55
typedef long long ll;
ll w[N];
#define M 35
ll f[N][N][M];
void add(ll a[], ll b[])
{
static ll c[M];
memset(c, 0, sizeof c);
ll t = 0;
for(int i = 0; i < M; i++){
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
void mul(ll *a, ll b)
{
static ll c[M];
memset(c, 0, sizeof c);
ll t = 0;
for(int i = 0; i < M; i ++)
{
t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof(c));
}
inline int cmp(ll a[], ll b[])
{
for(int i = M-1; i >= 0; i--)
{
if(a[i] > b[i]) return 1;
else if(a[i] < b[i]) return -1;
}
return 0;
}
void Print(ll *a)
{
int k = M-1;
while(k && !a[k]) k--;
while(k >= 0) {
printf("%d", a[k--]);
}
}
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%lld", w+i);
for(int len = 3; len <= n; len ++)
{
for(int i = 1; i + len - 1 <= n; i++){
int j = i + len - 1;
f[i][j][M-1] = 1;
for(int k = i + 1; k < j; k++){
static ll tmp[M];
memset(tmp, 0, sizeof tmp);
tmp[0] = 1;
mul(tmp, w[i]);
mul(tmp, w[j]);
mul(tmp, w[k]);
add(tmp, f[i][k]);
add(tmp, f[k][j]);
if(cmp(tmp, f[i][j]) == -1){
memcpy(f[i][j], tmp, sizeof tmp);
}
}
}
}
Print(f[1][n]);
return 0;
}
输出具体方案
479. 加分二叉树
设一个 n 个节点的二叉树 tree 的中序遍历为(1,2,3,…,n),其中数字 1,2,3,…,n 为节点编号。
每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为 1。
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树 tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第 1 行:一个整数 n,为节点个数。
第 2 行:n 个用空格隔开的整数,为每个节点的分数(0<分数<100)。
输出格式
第 1 行:一个整数,为最高加分(结果不会超过int范围)。
第 2 行:n 个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
数据范围
n<30
输入样例:
5
5 7 1 2 10
输出样例:
145
3 1 2 4 5
这里我使用了g[]数组进行了记录,其实也可以不记录,然后再DFS里面搜索从哪里转移就行。
#include <bits/stdc++.h>
using namespace std;
#define N 35
int f[N][N];
int g[N][N];
int w[N];
int n;
void dfs(int l, int r)
{
if(l > r){
return ;
}
int root = g[l][r];
printf("%d ", root);
dfs(l, root - 1);
dfs(root + 1, r);
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", w+i);
for(int len = 1; len <= n; len ++){
for(int l = 1; l + len - 1 <= n; l++){
int r = l + len - 1;
if(len == 1) {
f[l][r] = w[l];
g[l][r] = l;
}
else
{
for(int k = l; k <= r; k++){
int left = k == l ? 1 : f[l][k-1];
int right = k == r? 1 : f[k+1][r];
int t = left * right + w[k];
if(t > f[l][r]){
f[l][r] = t;
g[l][r] = k;
}
}
}
}
}
cout << f[1][n] << "\n";
dfs(1, n);
return 0;
}
二维区间DP
321. 棋盘分割
将一个 8×8 的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了 (n−1) 次后,连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
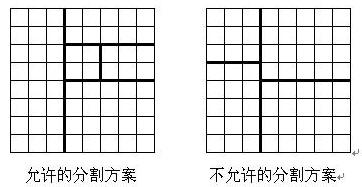
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n 块矩形棋盘,并使各矩形棋盘总分的均方差最小。

请编程对给出的棋盘及 n,求出均方差的最小值。
输入格式
第 1 行为一个整数 n。
第 2 行至第 9 行每行为 8个小于 100 的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出格式
输出最小均方差值(四舍五入精确到小数点后三位)。
数据范围
1<n<15
输入样例:
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
输出样例:
1.633
题解
在这一道题目中可以看到分治的影子。
切完一个之后转移到下一个小的区域。
在这里,是需要求解标准差差的最小值,等价于求解方差的最小值。
由于分母上的 n 已经给定,并且 x ˉ \bar{x} xˉ的值已经固定,所以仅仅需要让 ( x i − x ˉ ) 2 (x_i - \bar{x})^2 (xi−xˉ)2最小就可以了。
采用记忆化搜索:f[x1][y1][x2][y2][k]表示左上角坐标为(x1, y1),右下角坐标为(x2, y2)的区域,进行了
n
−
k
+
1
n - k + 1
n−k+1次剖分之后的
(
x
i
−
x
ˉ
)
2
(x_i - \bar{x})^2
(xi−xˉ)2的最小值。
#include <bits/stdc++.h>
using namespace std;
int n;
int a[10][10];
double f[10][10][10][10][18];
double avg = 0;
int s[10][10];
double count(int x1, int y1, int x2, int y2)
{
double res = 0;
res = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
return (res - avg)*(res - avg) / n;
}
double dfs(int x1, int y1, int x2, int y2, int k)
{
double &p = f[x1][y1][x2][y2][k];
if(p >= 0) return p;
if(k == 1){
p = count(x1, y1, x2, y2);
return p;
}
double minv = 1e30;
for(int i = x1; i < x2; i++){
minv = min(minv, dfs(x1, y1, i, y2, k - 1) + count(i + 1, y1, x2, y2));
minv = min(minv, dfs(i + 1, y1, x2, y2, k - 1) + count(x1, y1, i, y2));
}
for(int i = y1; i < y2; i++){
minv = min(minv, dfs(x1, y1, x2, i, k - 1) + count(x1, i + 1, x2, y2));
minv = min(minv, dfs(x1, i + 1, x2, y2, k - 1) + count(x1, y1, x2, i));
}
p = minv;
return p;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= 8; i++)
{
for(int j = 1; j <= 8; j ++){
scanf("%d", &a[i][j]);
}
}
for(int i = 1; i <= 8; i++){
for(int j = 1; j <= 8; j ++){
s[i][j] = a[i][j] + s[i][j-1] + s[i - 1][j] - s[i - 1][j - 1];
}
}
avg = (double)s[8][8] / n;
memset(f, -1, sizeof f);
printf("%.3lf\n", sqrt(dfs(1, 1, 8, 8, n)));
return 0;
}
改BUG记录:有时候觉得自己写的逻辑没有问题,这时候就要关注是不是某一个字母写成了另一个字母