基于R的Bilibili视频数据建模及分析——变量相关性分析篇

---

---

0、写在前面

实验环境

• Python版本：Python3.9
• Pycharm版本：Pycharm2021.1.3
• R版本：R-4.2.0
• RStudio版本：RStudio-2021.09.2-382

该实验一共使用4个数据集，但文章讲述只涉及到一个数据集，并且对于每个数据集的分析，数据大小在110条左右

• 数据来源于和鲸社区

https://www.heywhale.com/mw/dataset/62a45d284619d87b3b2b9147/file

数据字段描述说明

• title：视频的标题
• duration：视频时长
• publisher：视频作者
• descriptions：视频描述信息
• pub_time：视频发布时间
• view：视频播放量
• comments：视频评论数
• praise：视频点赞量
• coins：视频投币数
• favors：视频收藏数
• forwarding：视频转发量

1、数据分析

数据分析阶段一共分为三个角度进行分析，分别是变量相关性分析、聚类分析、建模-因子分析

下文先讲述变量相关性分析阶段

1.1 变量相关性分析

该阶段分为单元数据直观展示、多元数据直观展示以及多元数据与回归分析

1.2 单元数据直观展示

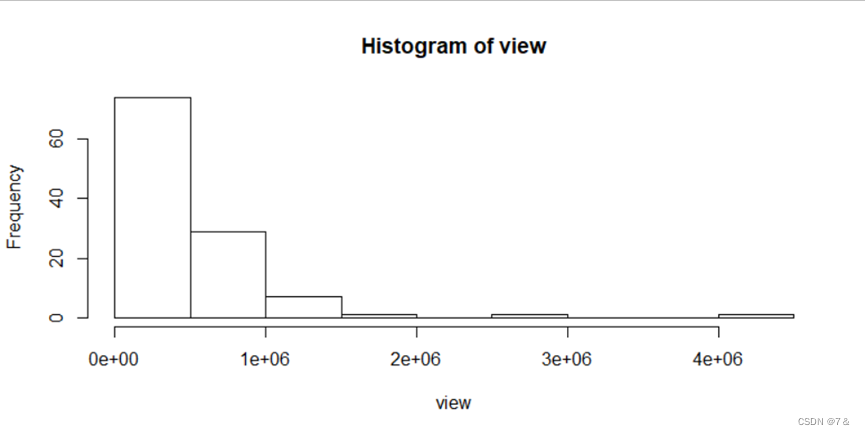
数据集1（单机游戏区）播放量view直方图：

data1 = read.csv("clipboard", header = T)
head(data1)
summary(data1)
attach(data1)
# view直方图
hist(view)

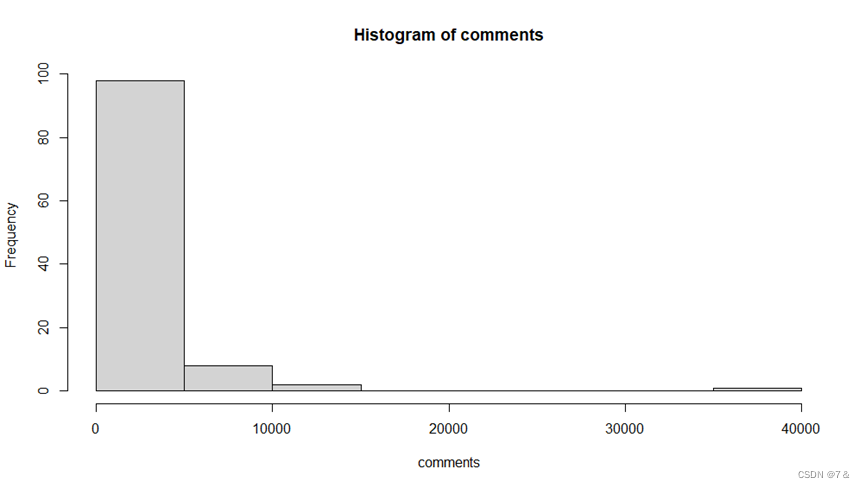
数据集2（搞笑生活区）评论数comments直方图：

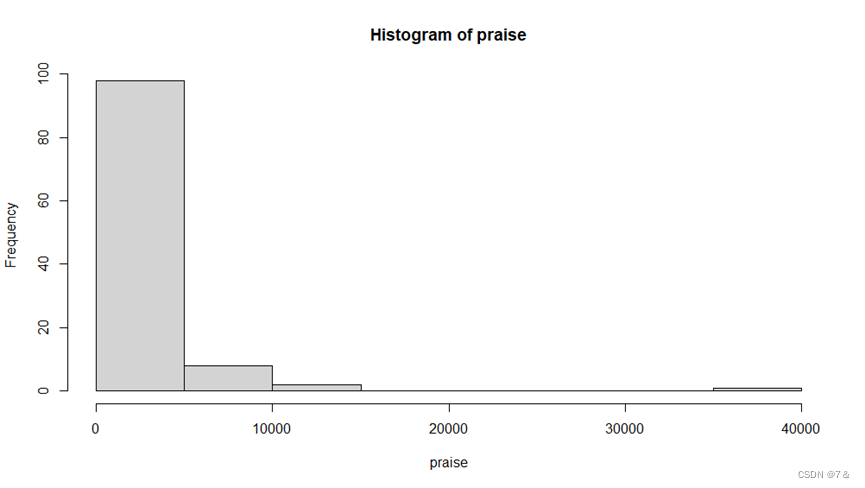
数据集3（数码科技区）点赞量praise直方图：

数据集4（影视杂谈区）评论数comments直方图：

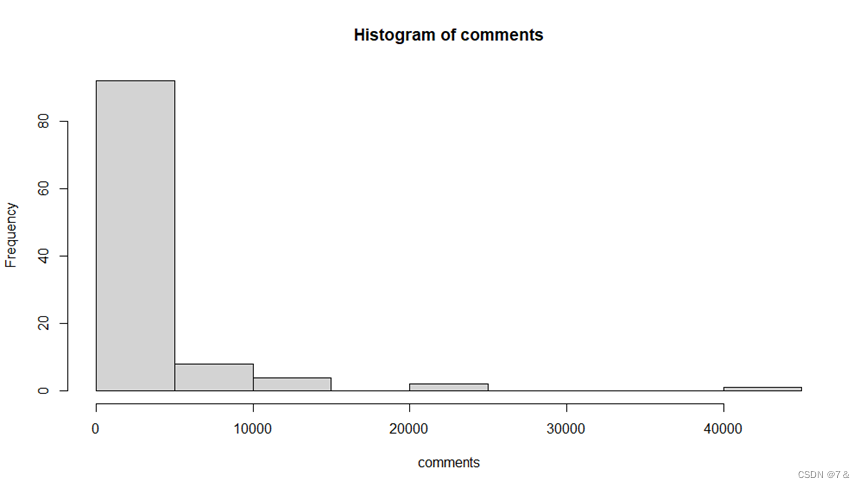
1.3 多元数据直观展示

• 按照列（view，comments，praise，coins，favors，forwarding）作均值饼图

pie(apply(data1[6:11], 2, mean))

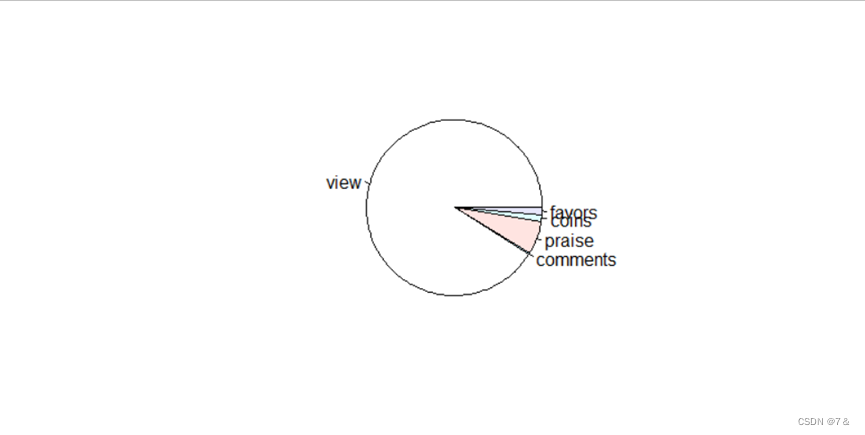
• 箱尾图：

boxplot(data1[6:11], horizontal = F)

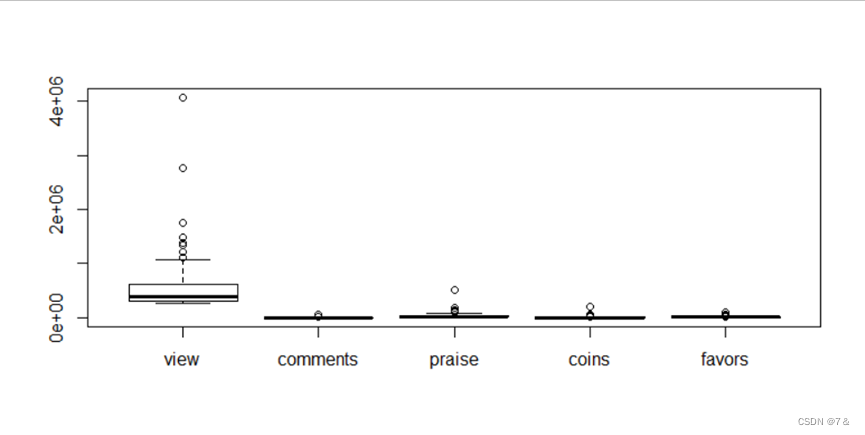
• 星相图：

stars(data1[6:11], full = F, draw.segments = T, key.loc = c(13, 1))

2、多元数据与回归分析

2.1 简单相关分析

针对数据集1，视频投币数coins与视频收藏量favors的相关分析与假设检验：

• 作散点图：

coinsArr = data1[,8]
favorsArr = data1[,9]
coins = c(coinsArr)
favors = c(favorsArr)
plot(coins, favors)

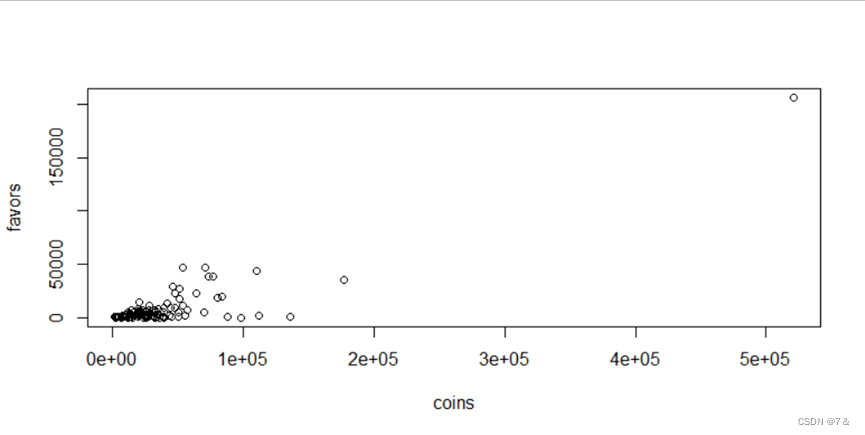
• 相关系数检验：

lxy <- function(x,y){
  n = length(x);
  sum((x/10000)*(y/10000)) - sum(x/10000)*sum(y/10000)/n
}
(r = lxy(coins,favors)/sqrt(lxy(coins,coins)*lxy(favors,favors)))

可以看到r值为正值，说明搞笑区的视频投币数和收藏量之间呈现正的线性相关关系。

n = length(coins)
tr = r / sqrt((1-r^2) / (n - 2))
cor.test(coins, favors)

由于P= 2.2e-16<0.05，于是在显著性水平ɑ=0.05上拒绝H0，接受H1，可认为单机游戏——游戏区中视频投币数和视频收藏量呈现正的线性关系。

2.2 简单线性回归分析

针对数据集1，拟合模型：

fm = lm(coins~favors, data = data1)
fm

得到回归方程为：coins^'= -3905.489 + 1.606favors

• 作回归直线：

plot(coins~favors, data = data1)

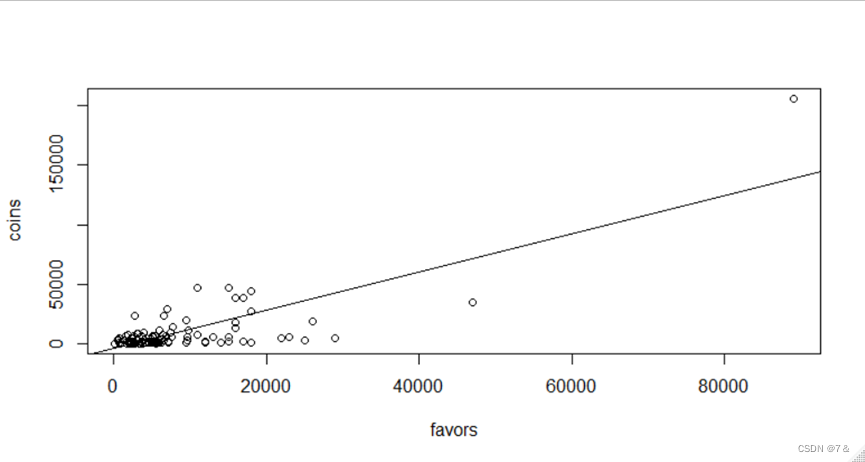
回归方程检验：

• 模型的方差分析：

abline(fm)
anova(fm)

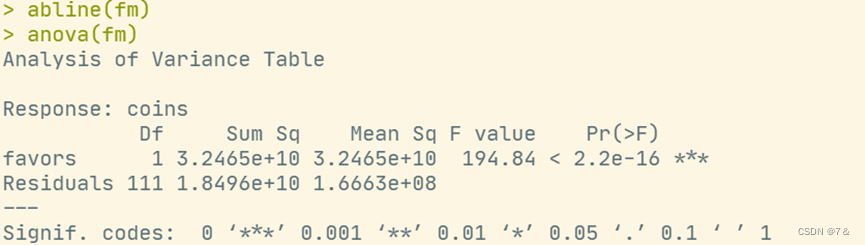
• 回归系数的t检验：

summary(fm)

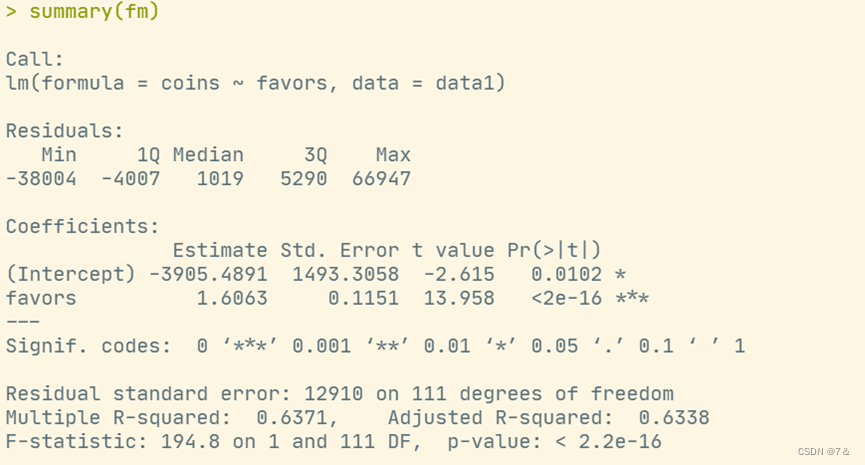
2.3 多元线性回归分析

针对数据集1

• 得到多元线性回归方程：

(fm1 = lm(view~praise+coins+favors+forwarding, data = data1))

view^'=179164.050+5.734praise-9.003coins+30.578favors+4.509forwarding

• t检验：

summary(fm1)

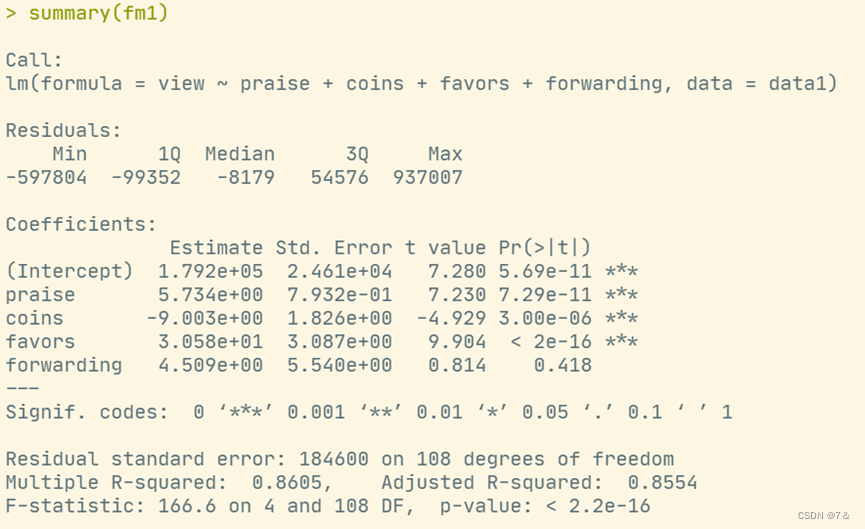
由方差分析结果可知，模型的P值<0.0001，故这个回归模型是有意义的。
同时由t检验结果可知，偏回归系数b1、b2、b3的P值都小于0.01，可以认为解释变量点赞量praise、投币数coins和收藏量favors显著。

逐步回归

fm1.step = step(fm1, direction = 'forward')
fm1.step = step(fm1, direction = 'backward')
fm1.step = step(fm1, direction = 'both')

• 向前引入法：

• 向后剔除法：

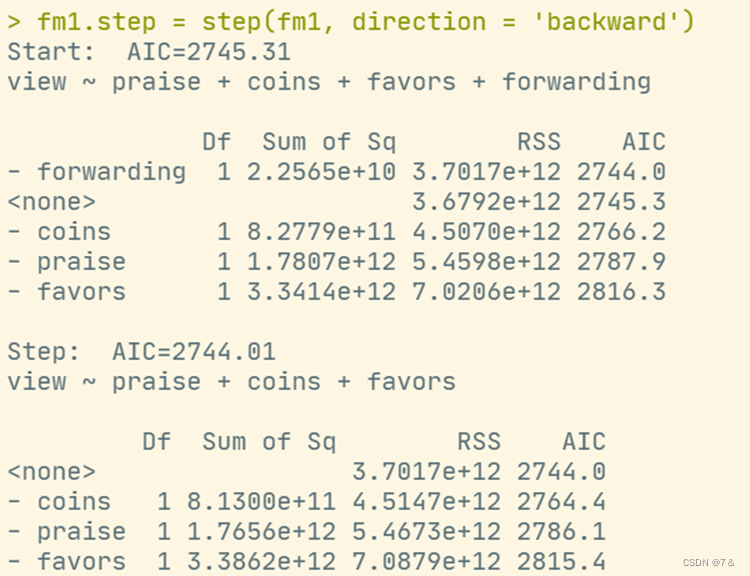
• 逐步筛选法：

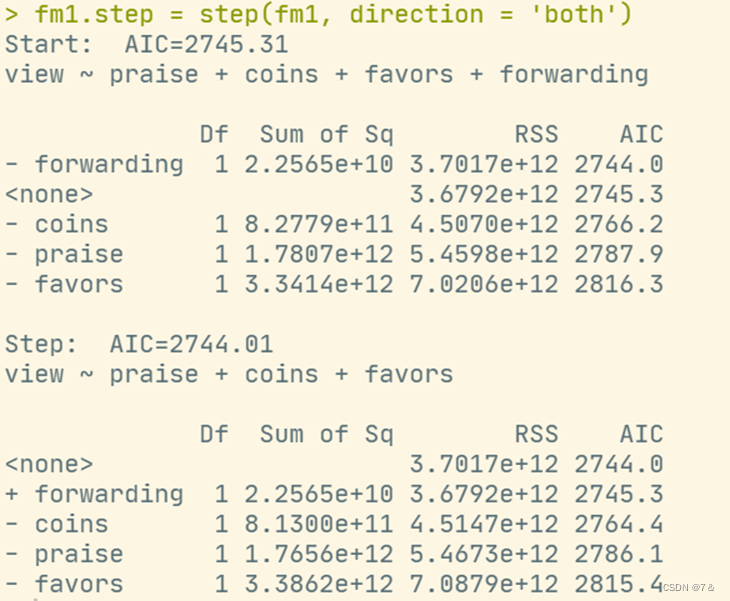
2.4 典型相关性分析

针对数据集1

data1_scale=scale(data1[6:11])
cor(data1_scale)
ca=cancor(data1_scale[,1:3],data1_scale[,4:6])
ca
# n:n行数据  p : X变量的个数 q:Y变量的个数
corcoef.test<-function(r, n, p, q, alpha=0.05){
  m<-length(r); Q<-rep(0, m); lambda <- 1
  for (k in m:1){
    lambda<-lambda*(1-r[k]^2);
    Q[k]<- -log(lambda)
  }
  s<-0; i<-m
  for (k in 1:m){
  }
  s<-0; i<-m
  for (k in 1:m){
    Q[k]<- (n-k+1-1/2*(p+q+3)+s)*Q[k]
    chi<-1-pchisq(Q[k],(p-k+1)*(q-k+1))
    abc=rbind(k,chi)
    print(abc)
    if (chi>alpha){
      i<-k-1
    }
    s<-s+1/r[k]^2
  }
}
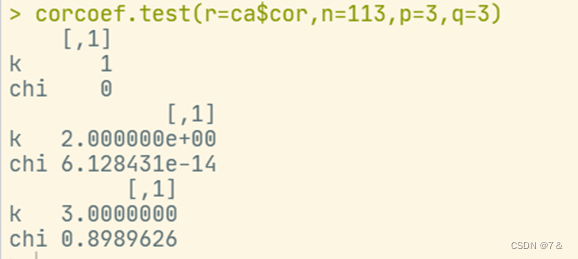
corcoef.test(r=ca$cor,n=113,p=3,q=3)

• 数据标准化：

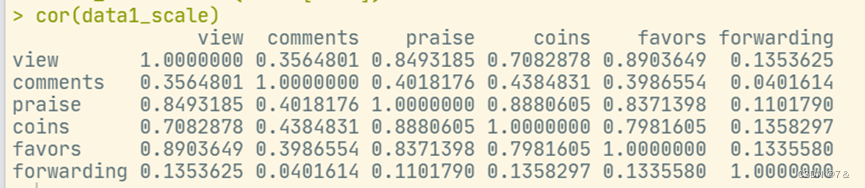
• cancor()方法的典型相关分析输出:

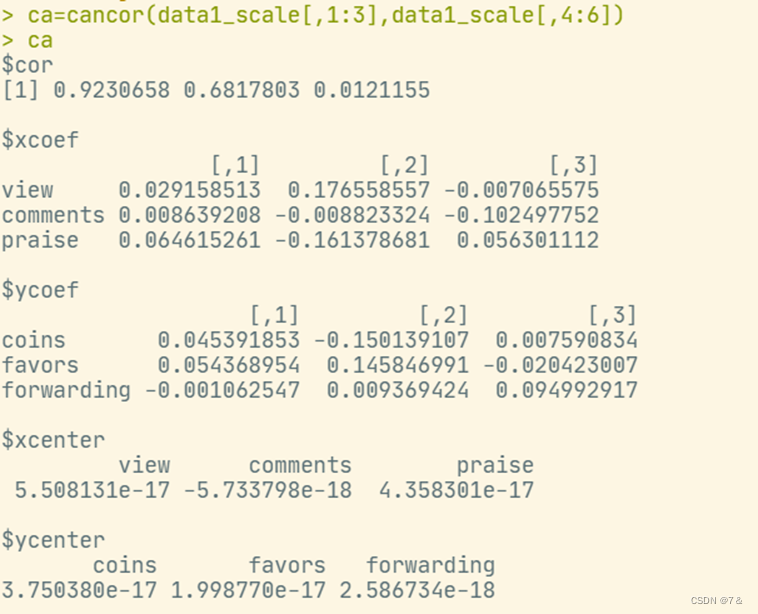
• test()结果:

3、参考资料

• 多元统计分析及R使用（第五版）

结束！