本文构建了包括不同的旋转角度、不同的叠层和两种不同布线方法（W 形和蛇形线）的测试手段，对应于这些设计的谐振是通过 VNA 测量获得的。然后，使用仿真方法来帮助我们理解这些实验结果。为了消除仿真与实验之间的差异，研究了由加工技术引起的一些实际因素，例如玻璃编织的不均匀性和蚀刻因素。仿真和实验取得了很好的一致性。本研究一方面可以帮助我们确定复杂PCB设计中引起谐振的主周期的长度，另一方面也可以在生产和设计两方面给出消除谐振的建议。最后，使用主动仿真来确认谐振对实际产品的影响。

介绍

玻纤的周期性排布以及layout周期性的布线会导致额外的走线损耗，这些损耗发生在传播信号的半波长的整数倍等于周期长度时，通常表现为插入损耗和回波损耗中的谐振。如果PCB的运行频率内出现了谐振，就会面临信号完整性问题。在实际的PCB设计中，为了避免玻纤效应带来的skew，设计者通常会旋转高速走线。为了节省layout空间，一些周期性的layout方法相继被使用，这些方法都会带来谐振。为了解决此问题，很多预测谐振频率和强度的方法被提出，基本的传输线理论可以很好地解释谐振原理，3D全波仿真也可以证明根据周期性的结构，简单的数值计算可以精确预测出谐振频率。然而，大多数早期研究是基于单层PCB模型，而不是高速产品的多层PCB模型，由于实际层压的复杂性，PCB加工过程的不确定性也会影响谐振。基于复杂的实际场景，需要新的仿真和实验，叠层/layout设计/材料特性以及加工技术都需要详细的讨论。

周期性结构导致的谐振

谐振频率和强度

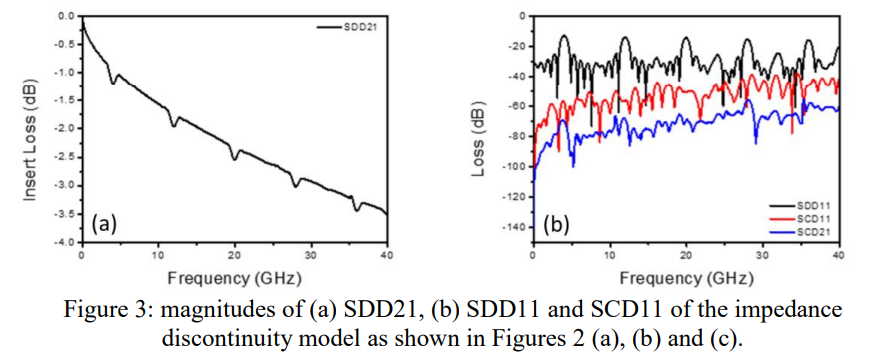
这里主要介绍由于周期性结构导致的差分对谐振，下图中，原始的SDD21曲线上就是被周期长度2cm的周期性结构引发的谐振。

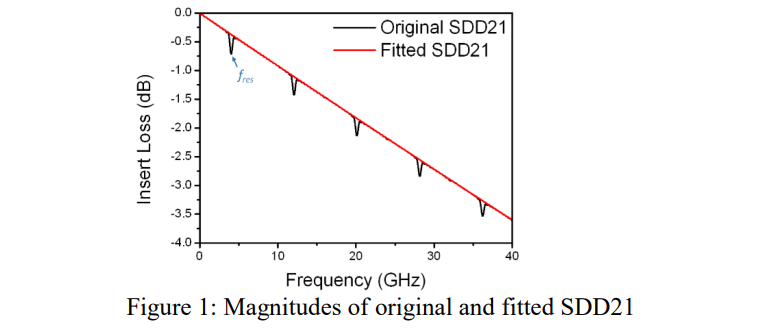
在原始SDD21曲线上有几处很明显的能量凹陷，谐振频率就是能量凹陷的最低点。根据传统的传输线理论，当传输线周期性变化时，在周期性不连续点会有额外的能量损失，当信号的波长等于周期长度的半个整数倍时，能量损耗最大，表现在插入损耗上就称为谐振。假设材料介电常数为Dk，由于周期性长度（Lperiod）导致的第一个谐振点频率f可以表示为：

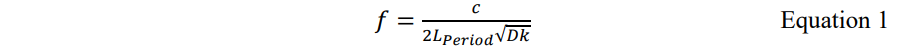
其中，c表示真空光速。

我们通过拟合方法消除了原始 SDD21 幅度的谐振，最终得到了拟合 SDD21 的幅度（红色曲线）。

可以通过比较原始 SDD21 和拟合的 SDD21 的大小来计算谐振强度。谐振频率（fres）下的谐振强度（I）可以表示为：

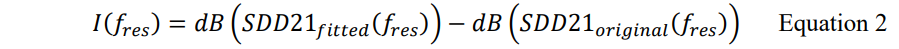
周期性结构导致谐振的机制

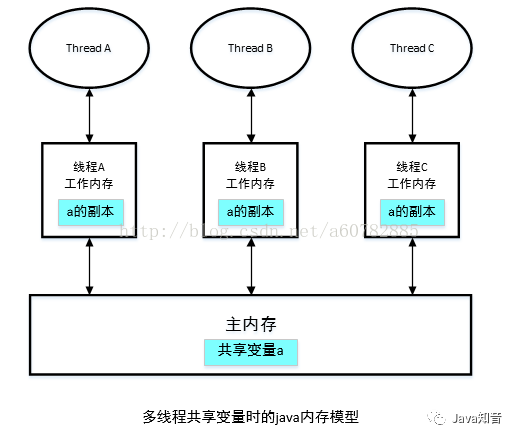
PCB的差分对中有两种谐振机制，一种是差分和共模转换导致的PN skew，一种是阻抗不连续。由周期性结构导致的谐振中，以上两种都会存在。所以我们使用两个简单的模型理解谐振和周期性结构的关系。下图a/b/c展示了由阻抗不连续引起的介电层的周期结构,d/e/f则展示了由于skew不连续引起的介电层周期结构。单个周期长度为2cm，包含两个单位的1cm，两个模型都是包含五个周期，在HFSS中建立这两个模型以获取S参数。

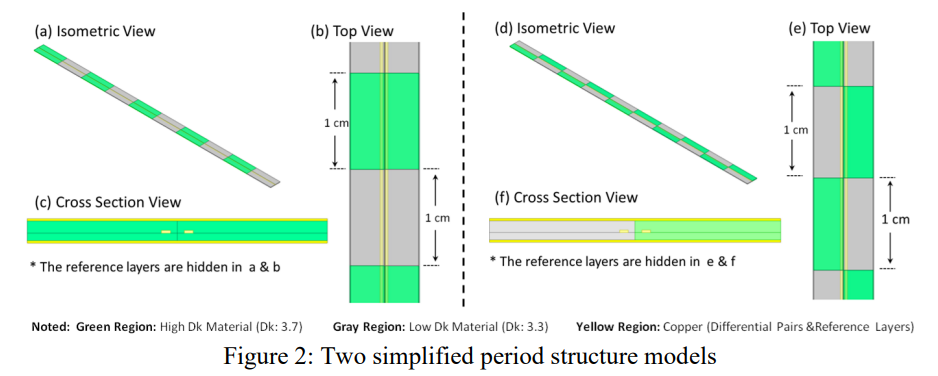
在阻抗不连续的模型中，因为绿色和灰色区域的Dk不同，两个区域的阻抗值也不同，因此在下图a中可以看到在很多频点下都有谐振，这是由于阻抗不连续引起的反射。在图b中可以看出来，有谐振的频点回损也有增加。因为此模型中P和N的信号传播速度一直保持一致，所以在SDC11和SDC21中就不存在差分和共模转换导致的额外损耗。第一个谐振点频率可以有公式一得出。

在skew不连续模型中，我们也可以看到SDD21曲线存在谐振，这些谐振点的频率和阻抗不连续模型中的频率几乎是一致的，回损曲线SDD11中并没有额外的能量损失，但比较明显的是在SDC11曲线的频点上有能量损失，这是因为差分对中的P和N在同一个横截面中，他们所处位置的Dk是不同的，在每个周期内，存在差分和共模之间的转换，这引起了额外的能量损失。谐振频率和总的skew相互独立，但是和周期长度有关，可以由公式1确认。

对于理想周期结构，不管谐振机制如何，相应的谐振频率有如下特征：

第一次谐振频率可以由公式1得出；

其余的谐振频率是第一个谐振频率的奇数倍。

PCB材料的周期性结构

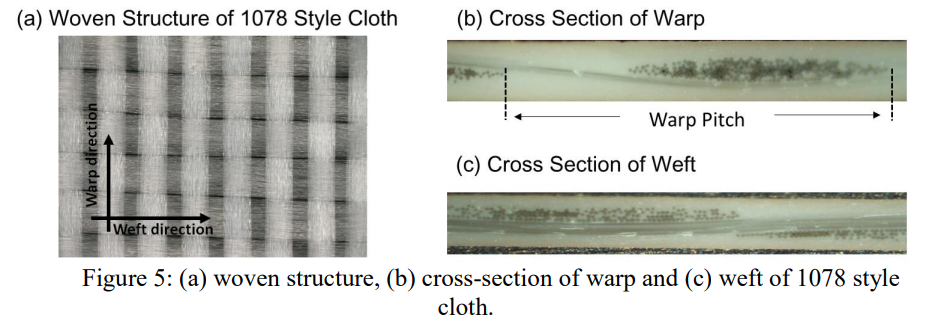
PCB的介质材料通常是由经向和纬向的玻璃束编织而成，然后填充树脂。这种编织形成了周期性的结构。这种结构中，树脂和玻纤的Dk显著不同，常规玻布的Dk为6.9，low-Dk玻布的Dk为4.8，而树脂的Dk小于3。另外，不同的加工技术下玻璃束的结构也不相同，主流有两种玻璃束，一种是传统的E玻布（E-glass），另一种是扁平玻布（MS-glass）。目前在高速PCB上常用的玻布是由E-glass（经向）和MS-glass（纬向）合制而成。下图a中展示了1078玻布的编织结构。图b和c分别是经向和纬向玻璃束的横截面，以图b经向为例，玻璃束的pitch就是在两个相邻的玻璃束中间，玻璃束宽度和树脂宽度的和。

上图b和c中的玻璃束区域是由玻璃丝和树脂组成，可以近似为一个椭圆区域，使用Intel的方法可以计算出该椭圆区域的Dkglass_eff，所以垂直等效Dk可以由下式得到：

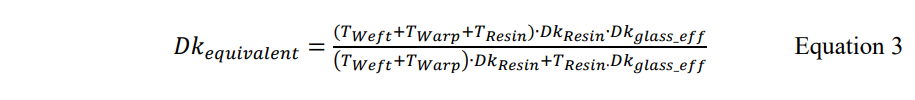
其中Tweft表示纬向玻璃束的厚度，Twarp表示经向玻璃束的厚度，Tresin表示树脂的厚度。通过公式3，我们将垂直方向的Dk投影到二维（2D）平面上，得到PCB材料的Dk周期分布，如下图所示。假设一个差分对穿过此周期性结构，在每个周期内都存在阻抗和skew不连续：如果将P和N看作一个整体，Dk沿着整个差分对呈周期性变化，导致差分阻抗也呈周期性变化，这和阻抗不连续模型比较类似。但是，如果将P和N看作不同的对象，在每个周期内P的Dk和N的Dk是都不同的，Dk可以影响P和N信号的传输速度，导致在每个周期内都有一个skew。这又和skew不连续模型比较类似。

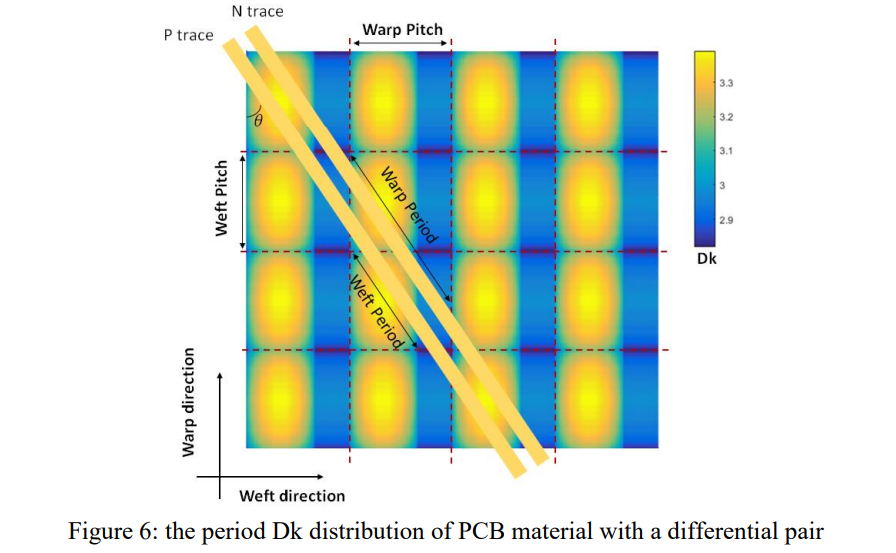
上图中，当差分对和经向玻璃束的夹角为，经向和纬向的周期长度可以由下式算出

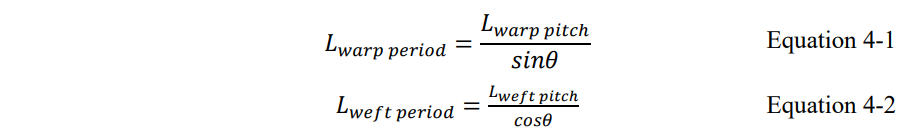
将差分对的总长固定，差分对经过经向和纬向玻璃束的周期数可以由下式算出

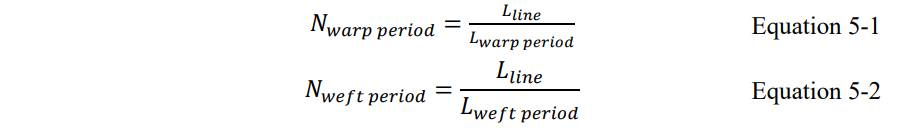
随着增加，经向周期长度减小，由经向导致的谐振频率会向高频方向移动，差分对经过经向玻璃束的周期数量增加，谐振强度也会增加，同时由纬向导致的谐振频率会呈相反方向变化。在下表中，经向和纬向的pitch可以由IPC规范得到。

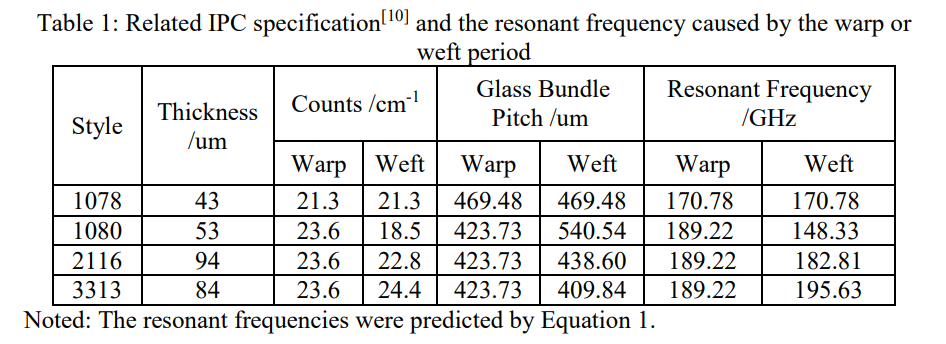
所有谐振频率预测的前提是单张玻布并且未旋转，如果叠层中由多张玻布，那么周期长度会比较复杂，下一章节中将会讨论。

现有的预测方法

在早期的出版物中，公式一是一个预测第一谐振点频率的有效方法，但是，这种数学方法仅仅考虑了谐振频率下板材Dk和玻璃束pitch的影响，无法给出谐振强度。

当考虑叠层/走线pitch和板材Df时，就必须使用3D模型，图5展示的实际编织模型仿真时太复杂，所以需要进行简化。有两种方法比较常用，一种是将玻璃丝转换成椭圆形玻璃束，另一种是直接使用具有不同 Dk 区域的简单方形模型。

这些早期的模型并没有考虑PCB加工端的因素，而且材料周期结构遇到周期布局设计的情况通常被忽略。