拓扑排序

讲拓扑排序前，我们要先了解什么是DAG树。所谓DAG树，就是指“有向无环图”。请判断下列图是否是DAG图

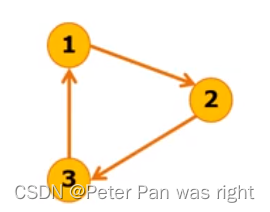
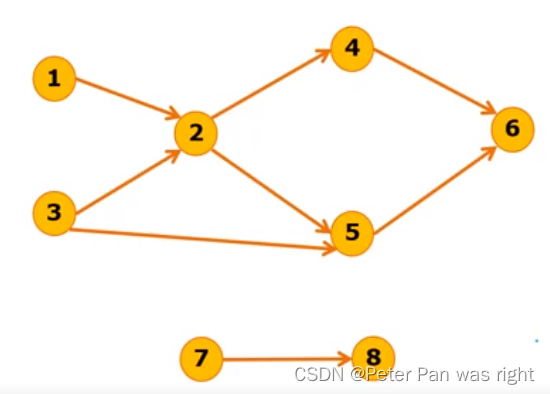
第一幅图，它不是DAG图，因为它形成了一个环。第二幅图，它也不是DAG图，因为它没有方向。第三幅图才叫真正的DAG图（DAG图不一定联通）。

那什么叫DAG图的拓扑排序呢？排序大家都知道。拓扑排序指，按照一定次序（箭头方向）来遍历这幅图。

我们看道题吧。

太戈编程877题

题目描述：

你是一个电子游戏高手，正在研究一款新的游戏。该游戏共有n种关卡有待解锁，编号1到n。你发现关卡的解锁有m条依赖关系，第i条为：解锁关卡ai前必须先解锁关卡bi。请你为n个关卡设计一个可行的解锁顺序，若有多个可行解请输出字典序最小解。本题保证有解。

这道题中，我们怎样画这幅图呢？我们遵守一个原则“若u和v有一条有向边，说明u必须在v之前访问”。那具体怎么解决呢？下面我们介绍两种方法：Kahn算法和DFS实现。

Kahn算法

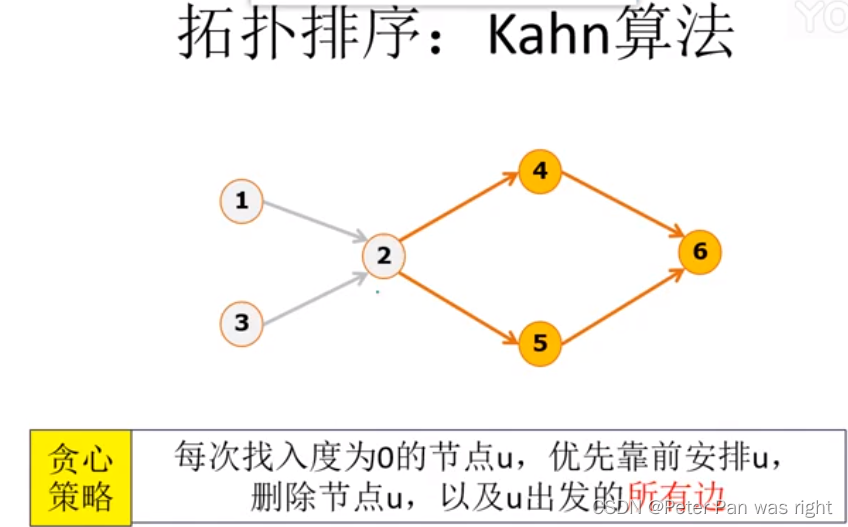
代码：

cin>>n>>m;
for(int i=1;i<=m;i++){
	int a,b;
	cin>>a>>b;
	if(d[b][a]) continue;//d[b][a]代表b要在a之前完成。易错点：重边处理
	d[b][a]=1;
	in[a]++;//in[a]代表关卡a的入度
}
for(int k=1,i;k<=n;k++){
	for(i=1;i<=n;i++) if(!vst[i]&&in[i]==0) break;
	topo[++cnt]=i;
	vst[i]=cnt;//vst[i]代表关卡i是否已解锁
	for(int j=1;j<=n;j++)
		if(d[i][j]) d[i][j]=0,in[j]--;
}
for(int i=1;i<=n;i++) cout<<topo[i]<<" ";

时空复杂度：O（N^2)

DFS

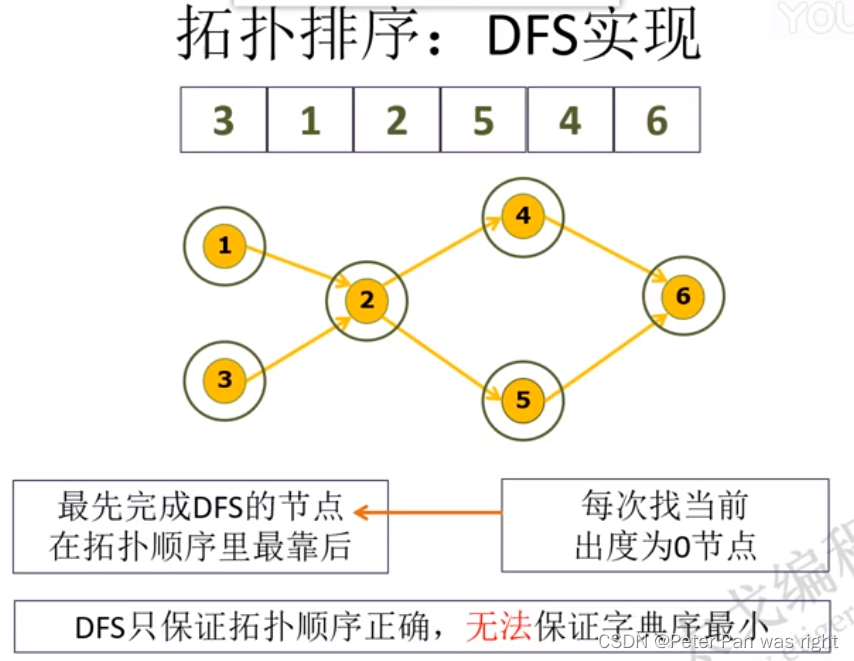
代码：

#include <bits/stdc++.h>
using namespace std;
const int N=10009;
vector<int> to[N];
int n,m,topo[N],cnt;
bool vst[N];
void dfs(int x){
	vst[x]=1;
	for(int i=0;i<to[N].size();i++){
		if(!vst[to[x][i]]) dfs(to[x][i]);
	}
	topo[n-cnt]=x;cnt++;
}
int main(){
	cin>>n>>m;
	for(int i=0;i<m;i++){
		int u,v;
		cin>>u>>v;
		to[u].push_back(v);
	}
	for(int i=1;i<=n;i++) if(!vst[i])dfs(i);
	for(int i=1;i<=n;i++) cout<<topo[i]<<" ";
	return 0;
}

我推荐使用DFS啊。练习：158、586。

后面来到我们的正（难）题：Minimum Spanning Tree 最小生成树

最小生成树

简称MST

在无向图中，任意两个顶点都有路径相通，称为连通图

连通图的生成树是包含原图n个顶和n-1条边的一棵树

最小生成树的所有边的长度综合是生成树里最小的

n个顶点的生成树有n-1条边，若再添加一条边，必定成环

大家算一下下列MST权值

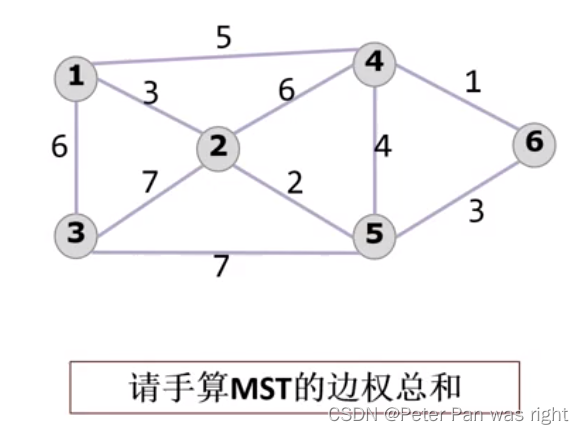
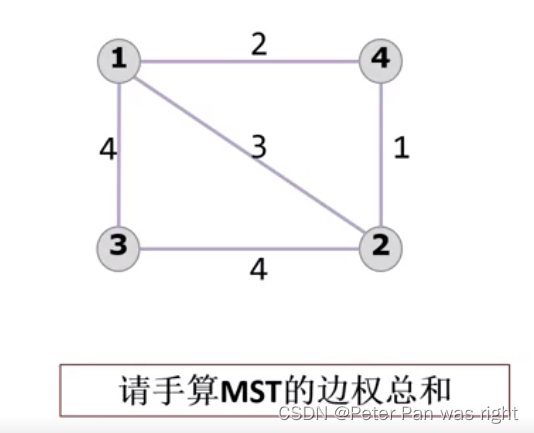
答案：15 7。我们注意到第一幅图有6个点，也就是生成树有5条边，312564。第二幅图有4个点，生成树有3条边，1423。

下面，我们将要教大家如何解决最小生成树问题

Kruskal算法

贪心：每次找最短边，尝试加入最小生成树。

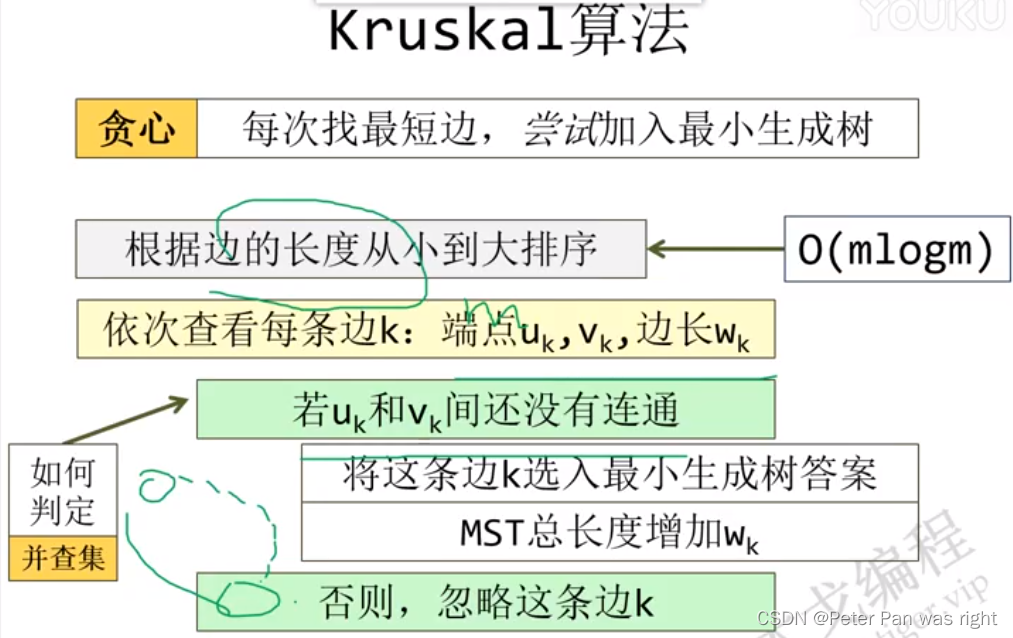
所以，大家要先会并查集，不会的小彭友看Peter算法小课堂—并查集-CSDN博客

给大家一个标程啊。

#include <bits/stdc++.h>
using namespace std;
const int N=109;
const int M=5009;
struct edge{int u,v,w;};
edge e[M];
int n,m,id[N];
int root(int u){
	return id[u]==u?u:id[u]=root(id[u]);
}
bool cmp(const edge&a,const edge&b){
	return a.w<b.w;
}
void Kruskal(){
	sort(e,e+m,cmp);
	for(int u=1;u<=n;u++) id[u]=u;
	int ans=0;
	for(int k=0;k<m;k++){
		int ru=root(e[k].u);
		int rv=root(e[k].v);
		if(ru==rv) continue;
		id[ru]=rv;
		ans+=e[k].w;
	}
	cout<<ans<<endl;
}
int main(){
	cin>>n>>m;
	for(int i=0;i<m;i++)
		cin>>e[i].u>>e[i].v>>e[i].w;
	Kruskal();
	return 0;
}

那有的人就会疑惑，为什么Kruskal算法能找到MST呢？下面给出证明。

请你证明：Kruskal选的第1条边e1一定在某棵MST中。

证：假设存在1棵不包含e1的MST记作T。向T中添加e1，必定成环。环中必有边长不小于e1的边f，删除f。新的生成树T+e1-f的边长总和不超过T，不符合最小条件。

可视化网址：最小生成树 MST （Prim算法，Kruskal算法） - VisuAlgo