Key Concept
图论是数学的一个分支,专注于研究图的性质和图之间的关系。在图论中,图是由顶点(或节点)以及连接这些顶点的边(或弧)组成的。图论的模型广泛应用于计算机科学、通信网络、社会网络、生物信息学、城市交通规划等多个领域。
图论的基本模型
-
无向图:
- 顶点之间的边没有方向。无向图常用于表示双向关系,如社交网络中的友谊关系。
-
有向图:
- 顶点之间的边有方向。有向图适用于表达方向性的关系,如网页间的链接。
-
加权图:
- 边或顶点被赋予权重(或成本、容量等)。加权图常用于道路网络,其中权重可以表示距离、时间、费用等。
-
多重图:
- 两个顶点之间可以有多条边。多重图适用于存在多种关系的场景,如航线图。
-
子图:
- 原图的一部分,包含原图的部分顶点和边。
-
完全图:
- 每对顶点之间都恰好有一条边。完全图用于当每个节点都与其他节点直接相连的情况。
-
树:
- 无环连通图。树常用于表示层次结构,如家族树或组织结构。
-
二分图:
- 顶点可分为两个互不相交的集合,图中的每条边连接的两个顶点分别属于这两个不同的集合。二分图适用于匹配问题,如工作分配或婚姻匹配。
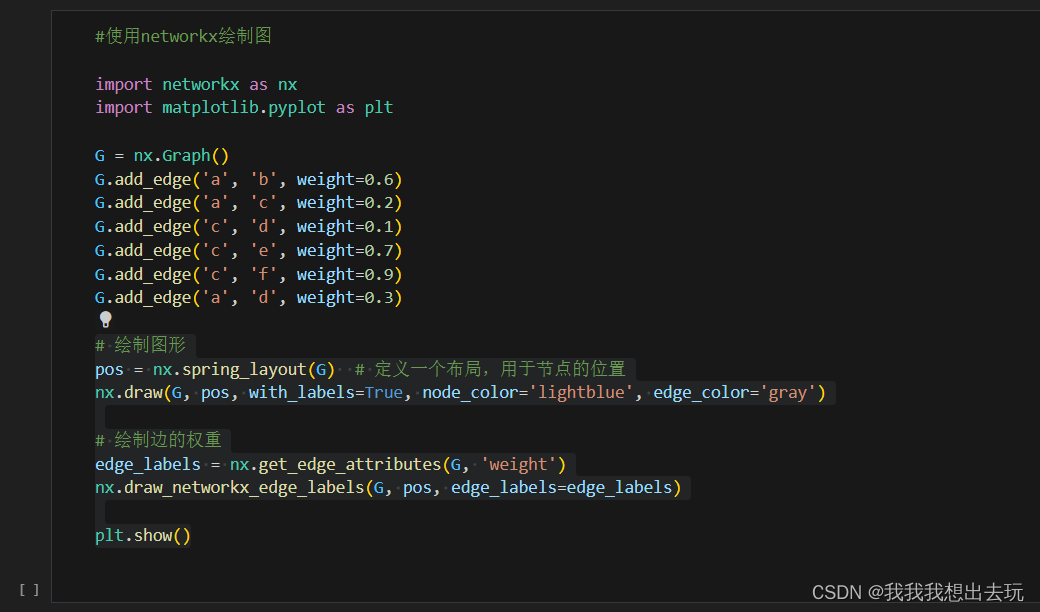
使用python的networkx库函数来绘制图

图论问题
-
最短路径问题:
- 在加权图中找到两点间的最短路径,如Dijkstra算法或Bellman-Ford算法。

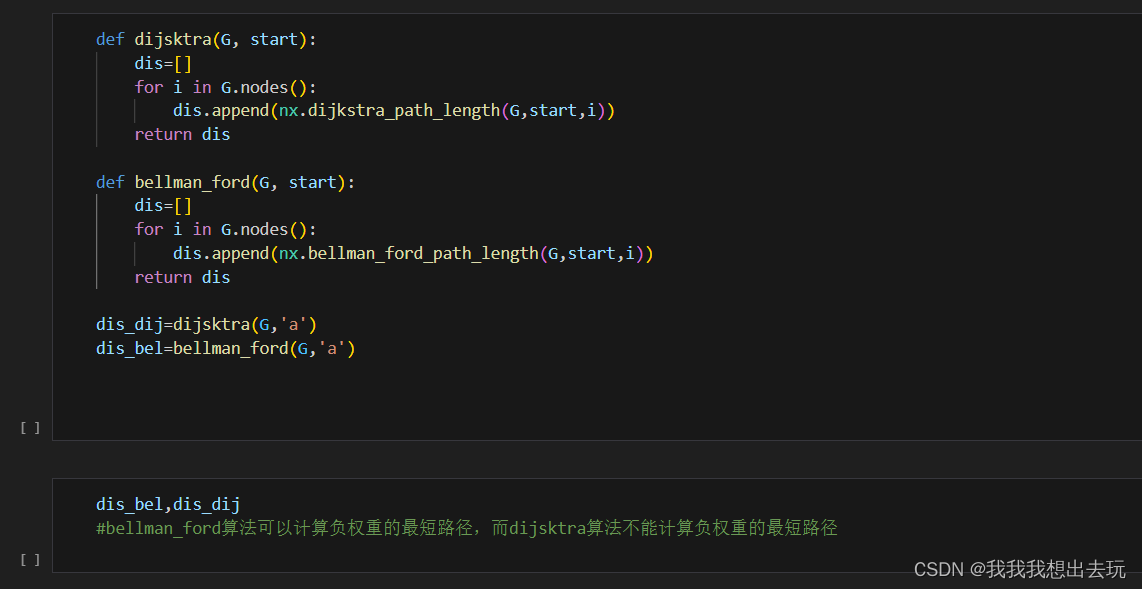
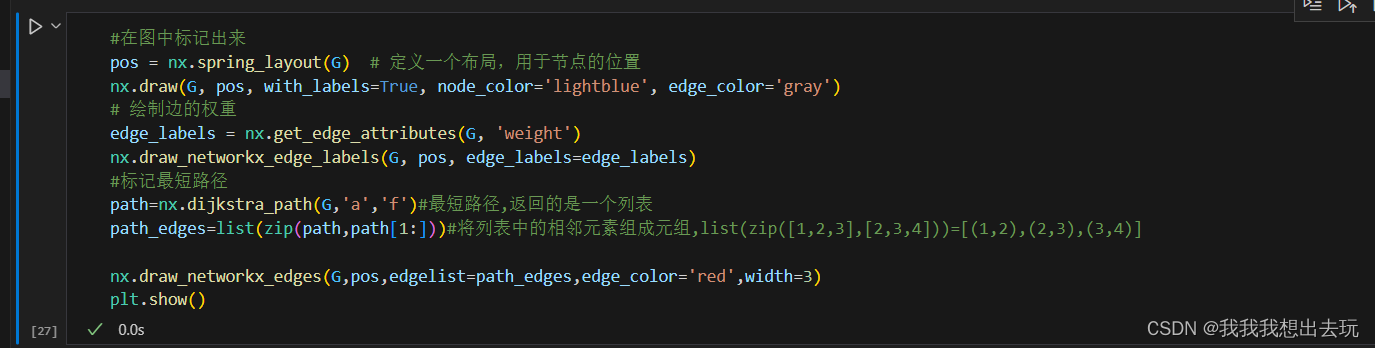

- 在加权图中找到两点间的最短路径,如Dijkstra算法或Bellman-Ford算法。
-
最小生成树
最小生成树这里有两种算法krual算法和prime算法
krual算法更适合稀疏图配合并查集来实现
prime算法更适合稠密图,直接对边进行遍历
#prim算法,更加适合稠密图
#1.任选一个顶点作为起始点,然后找到与其相连的最小权重的边,将这条边加入最小生成树中
#2.然后找到与这两个顶点相连的最小权重的边,将这条边加入最小生成树中
#3.重复上一步,直到所有的顶点都在最小生成树中
#4.最后得到的就是最小生成树
def prim(G):
mst = []
nodes = list(G.nodes())
visited = set([nodes[0]]) # 使用集合来快速检查是否访问过
while len(visited) != len(nodes):
min_edge = None
min_weight = float('inf') # 设置一个很大的初始值
for u in visited:
for v in G.neighbors(u):
if v not in visited and G[u][v]['weight'] < min_weight:
min_weight = G[u][v]['weight']
min_edge = [u, v, {'weight':G[u][v]['weight']}]
if min_edge is not None:
mst.append(min_edge)
visited.add(min_edge[1]) # 添加新顶点到访问过的集合中
return mst
# 假设G是已经创建好的图
mst = prim(G)
mst#krual算法,更加适合稀疏图
#1.将所有的边按照权重从小到大排序
#2.从权重最小的边开始,如果这条边的两个顶点不在同一个连通分量中,则将这条边加入最小生成树中,否则不加入
#3.重复上一步,直到所有的顶点都在同一个连通分量中
#4.最后得到的就是最小生成树
#这里使用并查集来实现查找连通分量
class UnionFind:
def __init__(self, nodes):
self.parent = {node: node for node in nodes}#初始化每个节点的父节点都是自己
def find(self, node):
if self.parent[node] != node:
self.parent[node] = self.find(self.parent[node])
return self.parent[node]
def union(self, node1, node2):
root1 = self.find(node1)
root2 = self.find(node2)
if root1 != root2:
self.parent[root2] = root1
def kruskal(G):
mst = []
edges = list(G.edges(data=True))
edges.sort(key=lambda x: x[2]['weight'])
uf = UnionFind(G.nodes())
for edge in edges:
u, v = edge[0], edge[1]
if uf.find(u) != uf.find(v): # 如果u和v不在同一个集合中
uf.union(u, v) # 合并集合
mst.append(edge) # 加入最小生成树
if len(mst) == len(G.nodes()) - 1:
break
if len(mst) != len(G.nodes()) - 1:
print('该图不是连通图')
return mst
mst=kruskal(G)
mst
-
网络流问题:
-
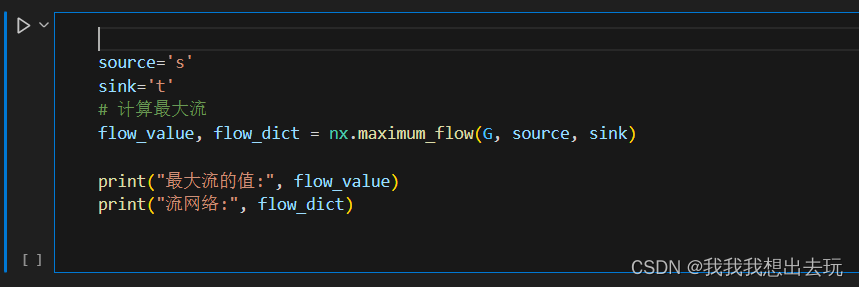
最大流问题
#网络最大流问题 #最大流问题是指在一个网络中,从源点到汇点的最大流量是多少 #1.将所有的边的流量初始化为0 #2.在残余网络中找到一条增广路径,如果没有增广路径,则结束 #3.在增广路径上找到最小的残余容量,将这个容量增加到这条路径上 #4.重复上一步,直到没有增广路径 #5.最后得到的就是最大流 import networkx as nx import matplotlib.pyplot as plt G = nx.DiGraph() G.add_edge('s', 'a', capacity=3.0) G.add_edge('s', 'b', capacity=1.0) G.add_edge('a', 'c', capacity=3.0) G.add_edge('b', 'c', capacity=5.0) G.add_edge('b', 'd', capacity=4.0) G.add_edge('d', 'e', capacity=2.0) G.add_edge('c', 't', capacity=2.0) G.add_edge('e', 't', capacity=3.0) # 绘制图形 pos = nx.spring_layout(G) # 定义一个布局,用于节点的位置 nx.draw(G, pos, with_labels=True, node_color='lightblue', edge_color='gray') # 绘制边的权重 edge_labels = nx.get_edge_attributes(G, 'capacity') nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels) plt.show()这里直接调用networkx来解决问题
-
-
最大流最小费用问题

#最小费用最大流问题 #最小费用最大流问题是指在一个网络中,从源点到汇点的最大流量是多少,且最小费用是多少 #1.将所有的边的流量初始化为0 #2.在残余网络中找到一条增广路径,如果没有增广路径,则结束 #3.在增广路径上找到最小的残余容量,将这个容量增加到这条路径上 #4.重复上一步,直到没有增广路径 #5.最后得到的就是最大流 #6.计算最小费用 #7.重复上述步骤,直到最小费用不再减少 import networkx as nx import matplotlib.pyplot as plt import numpy as np L = [('vs','v2',5,3),('vs','v3',3,6),('v2','v4',2,8),('v3','v2',1,2),('v3','v5',4,2), ('v4','v3',1,1),('v4','v5',3,4),('v4','vt',2,10),('v5','vt',5,2)] G = nx.DiGraph() for i in range(len(L)): G.add_edge(L[i][0], L[i][1], capacity=L[i][2], weight=L[i][3]) flow_dict = nx.max_flow_min_cost(G, 'vs', 'vt') min_cost = nx.cost_of_flow(G, flow_dict) node = list(G.nodes()) n = len(node) A = np.zeros((n,n), dtype=int) for i, adj in flow_dict.items(): for j, f in adj.items(): A[node.index(i), node.index(j)] = f print("最小费用最大流为:\n", flow_dict) print("最小费用为:\n", min_cost) print("最大流的流量为:\n", sum(A[:, -1])) print("最小费用最大流的邻接矩阵\n", A)
Key Concept Explanation 图论的模型和问题对于理解和解决现实世界中的复杂关系和网络结构具有重要意义。通过将实际问题抽象为图论问题,我们可以应用数学理论和算法来找到有效的解决方案。图论的应用范围非常广泛,从互联网的数据传输到社交网络的分析,再到交通网络的优化,都可以见到图论模型的影子。