课程目标
- 了解树/图的深度遍历,宽度遍历基本原理;
- 会使用python语言编写深度遍历,广度遍历代码;
- 掌握拓扑排序算法
搜索算法的意义和作用
搜索引擎
提到搜索两个子,大家都应该会想到搜索引擎,搜索引擎的基本工作步骤;
网页爬取 — 数据预处理 — 排序 — 查询
第一步,网页爬取,非常重要,简单来说,就是给爬虫(蜘蛛程序或者爬虫机器人)分配一组起始的网页,爬取一个网页后,解析提取出这个网页里的所有超链接,再依次爬取出这些超链接,再提取网页超链接,如此不断重复,从而提取网页内容。
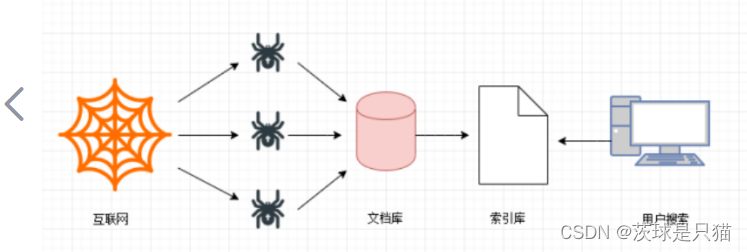
海量的网页链接之间最终构成了一张图,于是问题就变成了如何遍历这张图。
现在的网络,网站机构复杂,信息太多,所以蜘蛛爬行也是有一定策略的。基础就是广度优先和深度优先两种。现实确实时间和带宽优先,再大的搜索引擎也仅仅只能是收入小部分网页。提升网络爬虫的主要方法有:提升网站权重/频繁更新/导入链接/减短与首页的距离等等。
深度优先搜索DFS
定义与基本内容
深度优先搜索属于图算法的一种(Depth First Search)。其过程简要来说就是对每一个可能的分支路径深入到不能深入为止,而且每一个节点只能访问一次。
深度优先搜索是每一次按照一个方向进行穷尽式的搜索,当该方向上的搜索无法继续往前的时候,这时候就退回到上一步,换一个方向继续搜索。
算法演示如下:
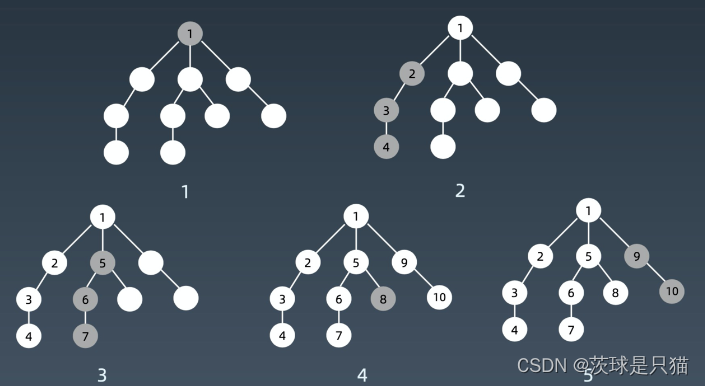
树的深度优先搜索
从跟节点开始,一直搜索左子树,直到某个节点没有左子树为止,接着换个方向搜索右子树。如图,
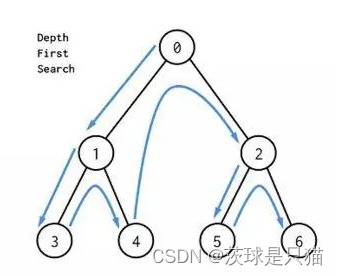
DFS的序列为(先序遍历):0 —> 1 —> 3 —> 4 —> 2 —> 5 —> 6
无向图的深度优先搜索
假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。
若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
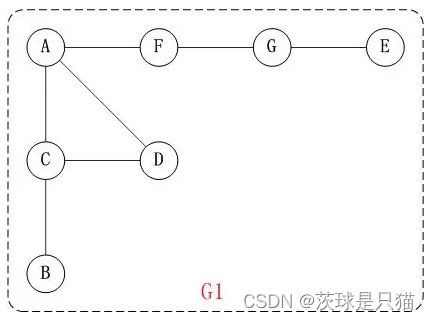
从顶点A开始深度优先搜索;
- 访问A;
- 访问A的相邻节点C
- 访问C的相邻节点B
- 在步骤3中访问了C的邻节点B之后,B周围没有邻节点未被访问;因此返回C节点,访问C的另一个邻节点D;
- 在步骤4中访问了D后,D周围没有未被访问的邻接点,因此返回C,再返回A,访问F;
- 访问F的邻接点G
- 访问G的邻接点E
访问的顺序:A—C—B—D—F—G—E
有向图的深度优先搜索
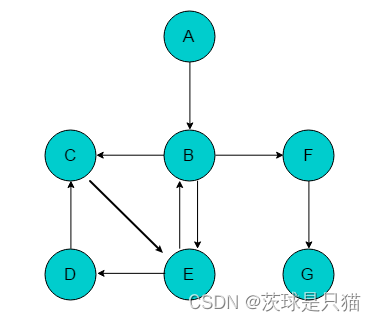
- 步骤1,访问A
- 步骤2,访问A的出边的顶点B
- 步骤3,访问B的出边的顶点C
- 步骤4,访问C的出边的顶点E
- 步骤5,访问E的出边的顶点D和B(B在步骤2中已经访问过了)所以访问D
- 步骤6,返回之前的节点,直到碰到还有未访问的出边顶点,所以访问到B的出边顶点F
- 步骤7,访问G
访问顺序:A—B—C—E—D—F—G
典型题目(200. 岛屿数量)
https://leetcode.cn/problems/number-of-islands/description/

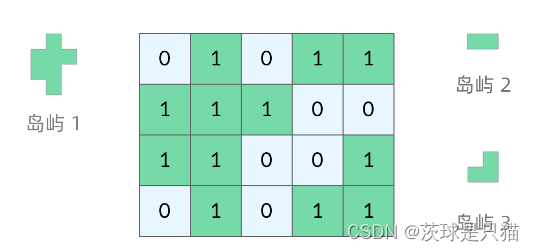
DFS(深度优先搜索)问题通常在树或者图结构上进行的,而这道提属于网络结构,网络结构要比二叉树结构稍微复杂,它其实是一个简化版的图结构。
分析:
- 访问相邻节点:网络结构中,上下左右四个位置都是相邻节点。坐标为(x, y)的格子,其四个相邻的格子分别为(x-1,y) (x+1,y) (x,y-1) (x,y+1)
- 判断base case:如果走进超出网格返回的格子,那么直接返回;
- 先往四个方向走一步再说,如果发现走出了网格范围再赶紧返回;
- 标记已经遍历过的格子。我们只关注值为1的格子做DFS遍历,每走过一个陆地格子,那就把格子的值改成0.
思路:
- 采用DFS方式:从(i,j)向此点的上下左右(i+1, j),(i-1, j), (i, j-1),(i, j+1)做深度搜索;
- 终止条件:①(i,j)越过矩阵边界;②非陆地
- 搜索岛屿的同时,将遍历过的地方改为0,以免重复搜索相同岛屿
主循环:
遍历整个矩阵,当遇到grid[i][j]==1时,从此点开始做深度优先搜索dfs,岛屿的数量+1且在深度优先搜索中删除此岛屿。
最终返回岛屿数量count。
class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
def dfs(grid, i, j, rows, cols):
# 退出条件
if i < 0 or i > rows - 1 or j < 0 or j > cols - 1 or grid[i][j] != "1":
return
grid[i][j] = '0'
dfs(grid, i, j+1, rows, cols)
dfs(grid, i, j-1, rows, cols)
dfs(grid, i+1, j, rows, cols)
dfs(grid, i-1, j, rows, cols)
rows = len(grid)
if rows == 0:
return 0
cols = len(grid[0])
num_islands = 0
for i in range(rows):
for j in range(cols):
# 只有确认时岛屿,才会遍历
if grid[i][j] == '1':
# 发现岛屿,岛屿个数加1
num_islands += 1
dfs(grid, i, j, rows, cols)
return num_islands