还在为管理众多店铺账号头疼?那你可就得了解一下多窗口同步这个功能了。想必很多卖家都遇到过需要同时打开多个窗口分别进行同步操作的问题,但有不少人不知道怎么做,今天龙哥就来为大家揭秘如何实现一键多窗口同步,掌握了技巧就会发现其实一点都不难!

多窗口同步的作用是什么?
首先我们需要知道什么是多窗口同步:
多窗口,顾名思义就是指在一个操作系统环境下,用户可以同时打开多个窗口进行不同的任务,并且这些窗口可以同时显示在屏幕上,让用户可以轻松地切换任务和处理不同的工作。多窗口同步就可以在多个窗口之间同步剪贴板、窗口大小、位置、状态等信息,例如,在不同的浏览器窗口中同时滚动或者放大缩小网页,让用户在多个窗口之间快速、方便地切换和操作。与传统的单窗口操作相比,多窗口同步器可以大大提高用户的工作效率和使用体验。
对于我们跨境卖家,尤其是拥有很多个店铺账号的卖家来说,多窗口同步这个功能就能发挥很大作用了。比如在平时运营多个店铺的时候我们都需要进行养号,利用这个功能,我们可以同时打开和管理多个店铺页面,在不同标签页之间同步执行点赞、评论等操作。这样就能大大提高工作效率,简化工作流程,让管理多个店铺变得更加轻松便捷。
如何实现多窗口同步?
俗话说,工欲善其事,必先利其器,很多技术哥会从技术层面来解决,比如敲代码这种方法,但对小白来说这种操作很麻烦也比较难上手,所以龙哥通常会使用一些工具来实现多窗口同步功能,像指纹浏览器AdsPower就具备了这一功能,它可以实现多个浏览器窗口一键排列、激活的功能,通过打开多个窗口,我们就可以在同一台设备上同时执行多项任务。使用鼠标、键盘、标签页、插件等工具时,所有操作都能同时进行,提高效率。

具体操作方法如下:
1、点击【新建浏览器】:想要打开多少个浏览器窗口就新建多少个。
2、在【账号管理】界面选需要的环境打开。
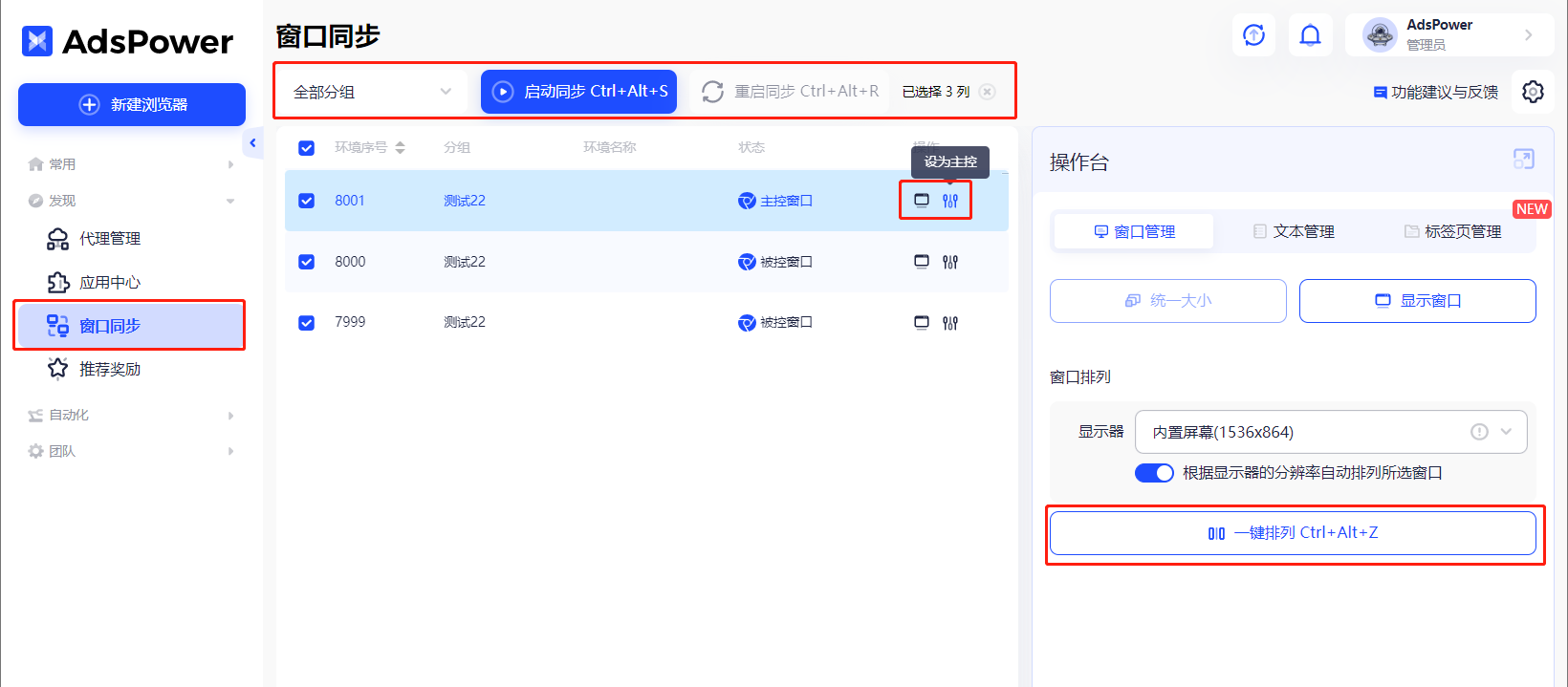
3、然后在【窗口同步】点击启动同步即可,系统会自动帮忙同步,快捷键:Ctrl+Alt+S。
4、如果觉得页面太乱就直接点击窗口同步中的【一键排列】,所有窗口将会整齐排列在显示器上。
总结
多窗口同步的功能对我们跨境卖家可以说是一个福音,在现在这个科技快速发展的社会,工具真的帮助了我们少走很多弯路,如果你经常需要同时打开多个窗口进行操作,不妨试试AdsPower,相信你会爱上它的便捷和高效。