手撕乘积(Multiplication & Product): 穷举和图示(2) 点积的几何意义
点乘
x = 3
y = 5
xNda = np.arange(x)
>>> array([0, 1, 2])
x2Nda = xNda*2+1
>>> array([1, 3, 5])
yNda = np.arange(1, y)
>>> array([1, 2, 3, 4])
xyNda = np.meshgrid(xNda, yNda)
>>> array([[[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]],
[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3]]])
np.dot(x, y)
>>> 15
np.dot(xNda, x)
>>> array([0, 3, 6])
np.dot(xNda+3, xNda+7) # 👇图示之
>>> 98
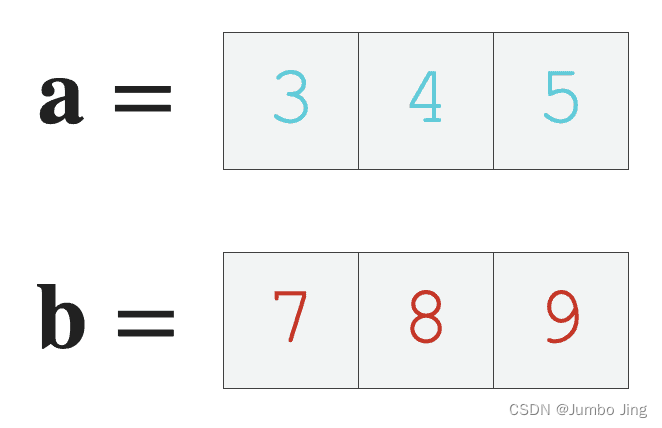
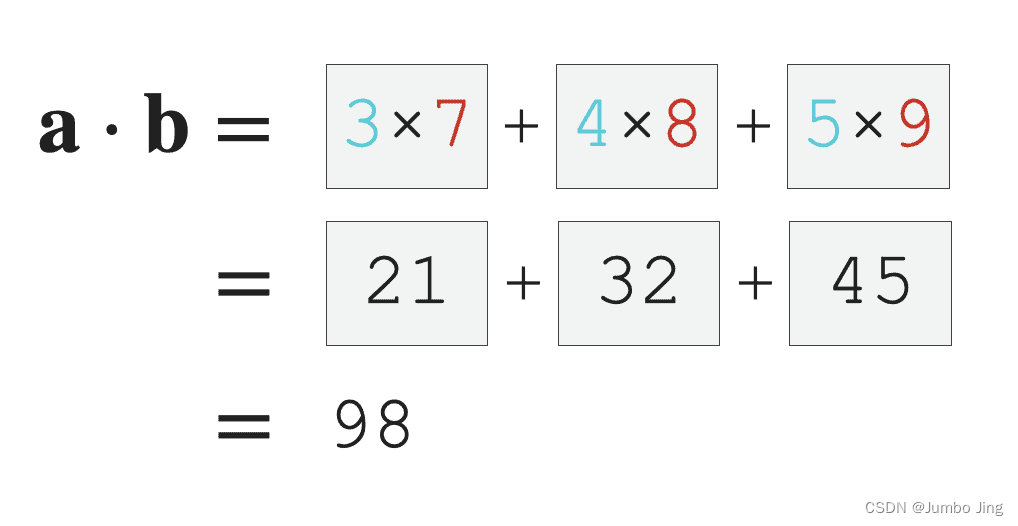
向量的点乘,也叫做向量的内积、数量积。对两个向量执行点乘运算,就是对着两个向量对应位置一一相乘之后求和的操作,点乘的结果是一个标量。
定义: 向量 a = [ a 1 , a 2 , . . . , a n ] a = [a_1, a_2, ..., a_n] a=[a1,a2,...,an] 和向量 b = [ b 1 , b 2 , . . . , b n ] b = [b_1, b_2, ..., b_n] b=[b1,b2,...,bn] 的内积为:
a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + . . . + a n b n a \cdot b = \sum_{i=1}^n a_i b_i = a_1 b_1 + a_2 b_2 + ... + a_n b_n a⋅b=∑i=1naibi=a1b1+a2b2+...+anbn
特别地, 0 ⋅ a = a ⋅ 0 = 0 0 \cdot a = a \cdot 0 = 0 0⋅a=a⋅0=0;若 a , b a, b a,b 是非零向量,则 a a a 与 b b b 正交的充要条件是 a ⋅ b = 0 a \cdot b = 0 a⋅b=0。
点积的几何意义: 可以用来表征或计算两个向量之间的夹角,以及在 b b b 向量在 a a a 向量方向上的投影,有公式:
a ⋅ b = ∣ a ∣ ∣ b ∣ cos θ a \cdot b = |a| |b| \cos \theta a⋅b=∣a∣∣b∣cosθ
其中, θ \theta θ 为 a a a 与 b b b 之间的夹角。

根据这个公式就可以计算向量 a a a 和向量 b b b 之间的夹角。从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:
- a ⋅ b > 0 a \cdot b > 0 a⋅b>0,方向基本相同,夹角在 0 ° 0° 0° 到 90 ° 90° 90° 之间;
- a ⋅ b = 0 a \cdot b = 0 a⋅b=0,正交,相互垂直;
- a ⋅ b < 0 a \cdot b < 0 a⋅b<0,方向基本相反,夹角在 90 ° 90° 90° 到 180 ° 180° 180° 之间。
向量点乘的运算特性:
- a 2 ≥ 0 a^2 \geq 0 a2≥0;当 a 2 = 0 a^2 = 0 a2=0 时,必有 a = 0 a = 0 a=0; (正定性)
- a ⋅ b = b ⋅ a a \cdot b = b \cdot a a⋅b=b⋅a;(对称性)
- ( λ a + μ b ) ⋅ c = λ a ⋅ c + μ b ⋅ c (\lambda a + \mu b) \cdot c = \lambda a \cdot c + \mu b \cdot c (λa+μb)⋅c=λa⋅c+μb⋅c,对任意实数 λ , μ \lambda, \mu λ,μ 成立; (线性)
- cos ∠ ( a , b ) = a ⋅ b / ( ∣ a ∣ ∣ b ∣ ) \cos \angle (a, b) = a \cdot b / (|a| |b|) cos∠(a,b)=a⋅b/(∣a∣∣b∣);(余弦定理)
- ∣ a ⋅ b ∣ ≤ ∣ a ∣ ∣ b ∣ |a \cdot b| \leq |a| |b| ∣a⋅b∣≤∣a∣∣b∣,等号只在 a a a 与 b b b 共线时成立。
代码解释点积的几何意义:
问题:
向量
a
=
[
1
,
0
]
a = [1, 0]
a=[1,0]和
b
=
[
1
,
2
]
b = [1, 2]
b=[1,2]两个向量之间的夹角是多少?
用图解释一下:
import matplotlib.pyplot as plt
ndA = np.asanyarray
a = ndA((1,1))
b = ndA((3,2))
o = ndA((0,0))
abAngle = np.degrees(np.arccos(np.dot(a,b)/(np.linalg.norm(a)*np.linalg.norm(b))))
print(f'abAngle={abAngle}°')
plt.axis('equal')
plt.grid()
plt.plot(*zip(o,a), 'r')
plt.plot(*zip(o,b), 'b')
plt.show()
np.dot(xNda, xNda)
>>> 5
- 💡: 自己点乘自己相当于求向量的模的平方 a ⋅ a = ∣ a ∣ 2 a \cdot a = |a|^2 a⋅a=∣a∣2。
# 向量的模长(即到原点的距离)
np.linalg.norm(xNda)
xDst = np.dot(xNda, xNda)**.5
判断向量 a ⃗ \vec{a} a与 b ⃗ \vec{b} b是否正交, 是否同向…
def v1v2(a, b):
dotAb = np.dot(a, b)
if dotAb == 0:
print('垂直')
elif dotAb > 0:
print('同向')
elif dotAb < 0:
print('反向')
if abs(dotAb) == 1:
print('平行')
标量投影
a b = ∣ a ∣ cos θ a_b = |a| \cos \theta ab=∣a∣cosθ
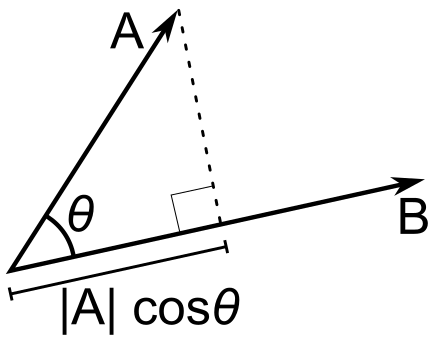
a b = ∣ a ∣ cos θ = a ⋅ b ∣ b ∣ = a ⋅ b ^ a_b = |a| \cos \theta = \frac{a \cdot b}{|b|} = a \cdot \hat{b} ab=∣a∣cosθ=∣b∣a⋅b=a⋅b^
# aPjb = lambda a, b: np.dot(a, b)/np.linalg.norm(b) * b/np.linalg.norm(b) # 向量a在向量b上的投影的标量(长度); 乘以向量b的单位向量, 得到向量a在向量b上的投影向量
aPjb = lambda a, b: b * np.dot(a, b)/np.dot(b, b) # 获取向量a在向量b上的投影点()
# 进一步简化, 已知b的单位向量
aPjbN = lambda a, bN: bN * np.dot(a, bN) # 获取向量a在向量b上的投影点()
- 注意⚠️: 👆🏻 a ⃗ \vec{a} a和 b ⃗ \vec{b} b的关系建立在笛卡尔坐标系, 原点o是起点.
引入第3点 c ⃗ \vec{c} c作为起点, 点>>线>>面, 让我们从起点o进入欧氏几何…
a + b
>>> array([4, 5])
c = ndA((1,3))
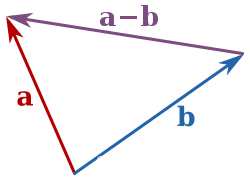
b - a
>>> array([2, 1])
a - b
>>> array([-2, -1])

```python
np.linalg.norm(a-b) # 欧氏距离
>>> 2.23606797749979
∠ a b c \angle{abc} ∠abc = ?
abLen = lambda: a_b: np.linalg.norm(a_b)
acbAngle = np.degrees(np.arccos(np.dot(a-c, b-c)/(np.linalg.norm(a-c)*np.linalg.norm(b-c))))
print(f'acbAngle={acbAngle}°')
a到bc的距离:
a2bcLen = abLen(a - aPjb(c-a, b-c))
升级继续, 让这些图形动起来:
点在空间中, 只有移动, 👇:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
o = ndA((0,0,0))
a = ndA((1,1,1))
b = ndA((3,2,1))
o + ndA((1, 0, 0)) # 表示o点在x轴上移动1个单位, y轴和z轴不变; 以此类推
def axMat(p, xyz='x', stp=1):
if xyz == 'x':
p1 = p + ndA((stp, 0, 0))
elif xyz == 'y':
p1 = p + ndA((0, stp, 0))
elif xyz == 'z':
p1 = p + ndA((0, 0, stp))
return p1
# 同理, plnMat, 三维空间中的平面移动;
def plnMat(p, xyz='xy', stp=ndA((1,1))):
if xyz == 'xy':
p1 = p + ndA((stp[0], stp[1], 0))
elif xyz == 'yz':
p1 = p + ndA((0, stp[0], stp[1]))
elif xyz == 'xz':
p1 = p + ndA((stp[0], 0, stp[1]))
return p1
# 如果都不为0, 就摆脱了轴和面的限制, 可以在空间中任意移动,,, 但是, 你得知道你要移动到哪里去...好无聊...我们先从二维的几何体开始
# 先建一个三角形abc
abcNda = ndA([[1,1], [3,2], [1,3]])
# tfMat = ndA([[r0c0, r0c1], [r1c0, r1c1]])
tfMat = lambda r0c0, r0c1, r1c0, r1c1: ndA([[r0c0, r0c1], [r1c0, r1c1]])
所谓的变换矩阵(Transformation matrix), '就是一个二维数组, 用来描述一个几何体的变换, 例如: 旋转, 缩放, 平移等等…, ’ (👈🏻小c![]() 插话)是一个(n,n)的数组, 好吧…其实呢, 我们只需要知道:2x2, 3x3和4x4这三种矩阵来完成欧几里得变换, 先从二维开始…
插话)是一个(n,n)的数组, 好吧…其实呢, 我们只需要知道:2x2, 3x3和4x4这三种矩阵来完成欧几里得变换, 先从二维开始…
未完待续…
以上内容来自维基百科, 由![]() 协助完成.
协助完成.


![[易语言]易语言部署yolox的onnx模型](https://img-blog.csdnimg.cn/direct/6f91a98289da4c2d825e1245af03ddc7.jpeg)