---

题402.数位dp-acwing-1082. 数字游戏

---

一、题目

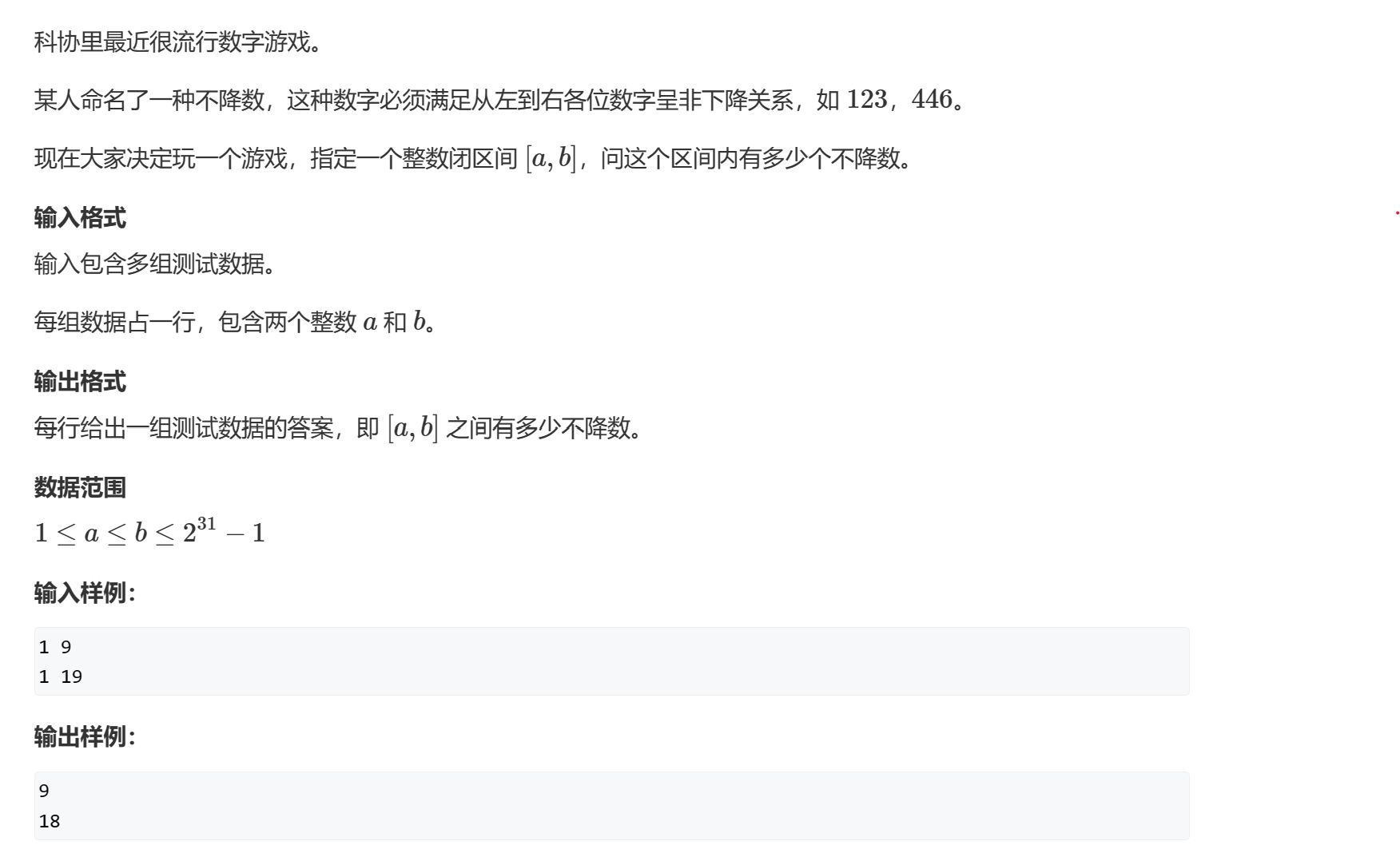
二、题解

欲求区间[X,Y]中满足性质的数的个数，我们可以想着去求小于m的数中满足性质的个数f(m)，然后利用前缀和思想，f(X,Y)=f(Y)-f(X-1)得到最后结果。
现在考虑如何求f(m):
对于上界m，设按B进制表示为a_n-1a_n-2a_n-3a_n-4…a₁a₀，则我们可以据此来给每一位填数，则以填最高位为例，新数该位要么填0-a_n-1-1(由于是要满足不降性质，因此最小只能填到上一位的数last)，要么填a_n-1(当然也需满足不降性质)，对于前者之后的位不论怎么填都可以满足比n来得小，则将满足性质的数的个数计入总的方案数，对于后者则last修改为当前位，然后须按照上述方式接着讨论，则整个过程可以按树讨论如下：

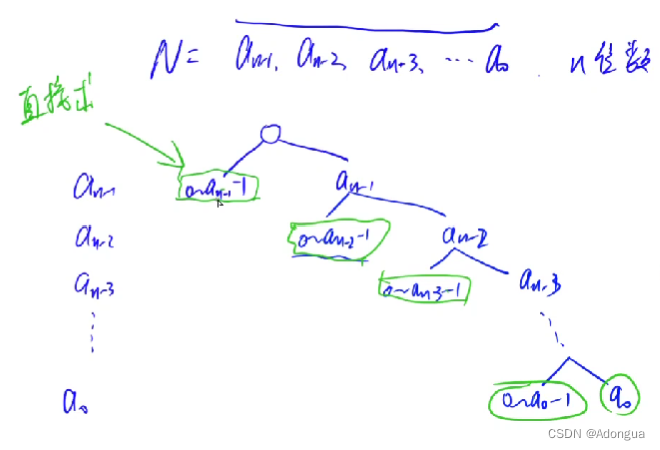
则我们还需开局预处理出给左分支使用的i位数时，最高位填j的结果f[i][j]，对此可以使用dp来实现，以下直接对递推公式分析，采用y式dp分析法：

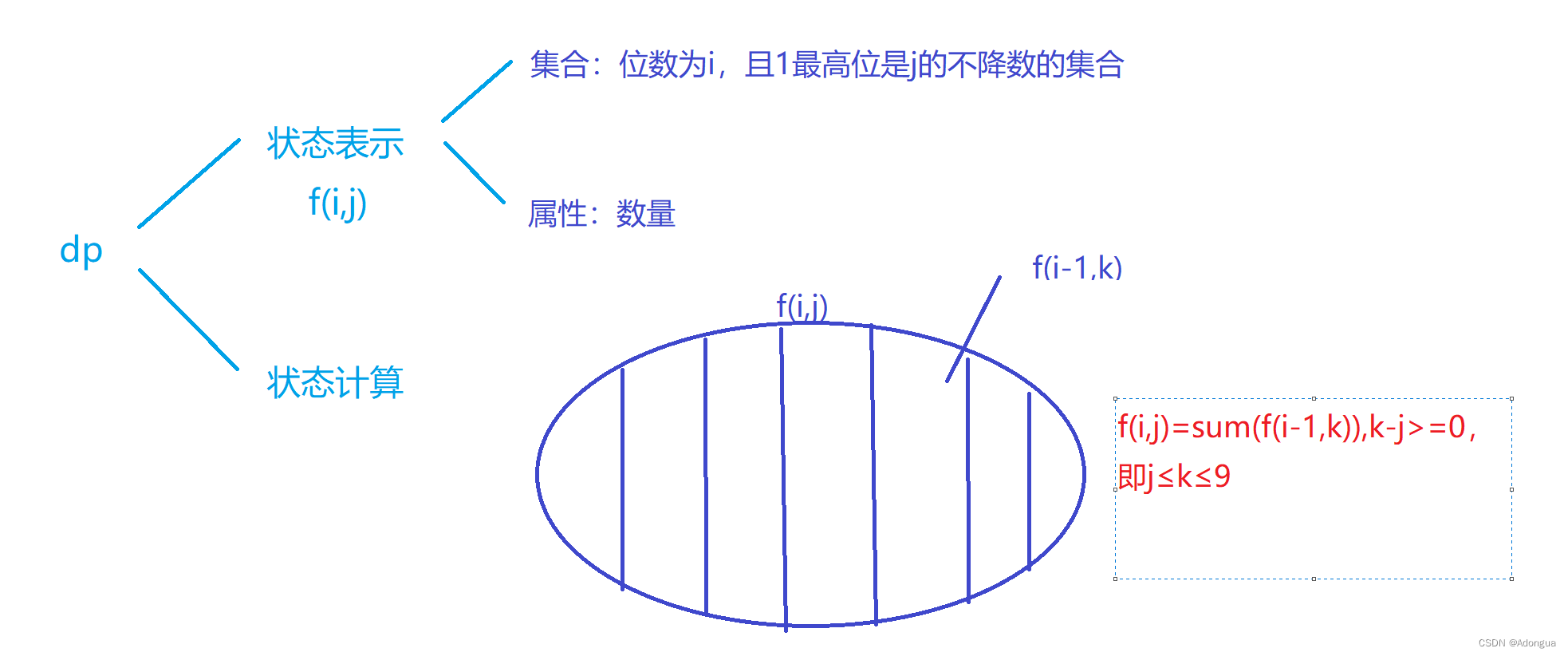
则代码如下：

#include <bits/stdc++.h>

using namespace std;

const int maxn=15;

int f[maxn][10];//f[i][j]表示i位数下最高位填j的方案数

void init()
{
    //初始化dp数组
    for(int i=0;i<=9;i++) f[1][i]=1;//1位数下最高位填i的方案数必定为1
    for(int i=2;i<maxn;i++)
    {
        for(int j=0;j<=9;j++)
        {
            for(int k=j;k<=9;k++)
            {
                f[i][j]+=f[i-1][k];//sum(1*f[i-1][k])
            }
        }
    }
}

int dp(int n)//求小于等于n的数中满足性质的数的个数
{
    if(!n) return 1;//上界为0时满足性质的数就是0，所以方案数为1

    //分离位数
    vector<int> nums;
    while(n) nums.push_back(n%10),n/=10;

    int res=0;
    int last=0;//last存储上一位填的数
    for(int i=nums.size()-1;i>=0;i--)//从最高位向低位枚举
    {
        int x=nums[i];
        for(int j=last;j<x;j++) res+=f[i+1][j];//左分支，res加上i+1位数下最高位填j（[max(0,last),x-1]）的方案数
        if(x<last) break;//右分支，填x，若x比last来的小则非法不填，直接break
        last=x;//
        if(!i) res++;//填到最后一位，方案数++
    }

    return res;
}

int main()
{
    init();
    int l,r;
    while(cin>>l>>r)
    {
        cout<<dp(r)-dp(l-1)<<endl;
    }
}

三、类似题目

1.acwing-1083. Windy数
（1）题目：

（2）代码：

#include <bits/stdc++.h>

#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=0;i--)
#define pb push_back

using namespace std;

const int maxn=11;

int f[maxn][10];

void init()
{
    rep(i,0,10) f[1][i]=1;
    rep(i,2,maxn)
    {
        rep(j,0,10)
        {
            rep(k,0,10)
            {
                if(abs(j-k)>=2) f[i][j]+=f[i-1][k];//注意是相差至少为2，不是当前位填的数一定要比上一位大2，所以是条件abs>=2
            }
        }
    }
}

int dp(int n)
{
    if(!n) return 0;
    vector<int> nums;
    while(n) nums.pb(n%10),n/=10;
    int res=0;
    int last=-2;
    per(i,0,nums.size())
    {
        int x=nums[i];
        rep(j,0,x)
        {
            if(!j&&i==nums.size()-1) continue;//刨去前导零的情况，这样最高位必为至少从1打头的数了
            if(abs(j-last)>=2) res+=f[i+1][j];
        }
        if(abs(x-last)<2) break;
        last=x;
        if(!i) res++;
    }
    rep(i,1,nums.size())//由于此前计入方案数时刨去前导零情况，所以这样要再做个特殊处理把因为前导0而成的(<n)位数方案计入
    {
        rep(j,1,10) res+=f[i][j];
    }
    return res;
}

int main()
{
    init();
    int l,r;
    cin>>l>>r;
    cout<<dp(r)-dp(l-1);
}

2.acwing-1085. 不要62
（1）题目：

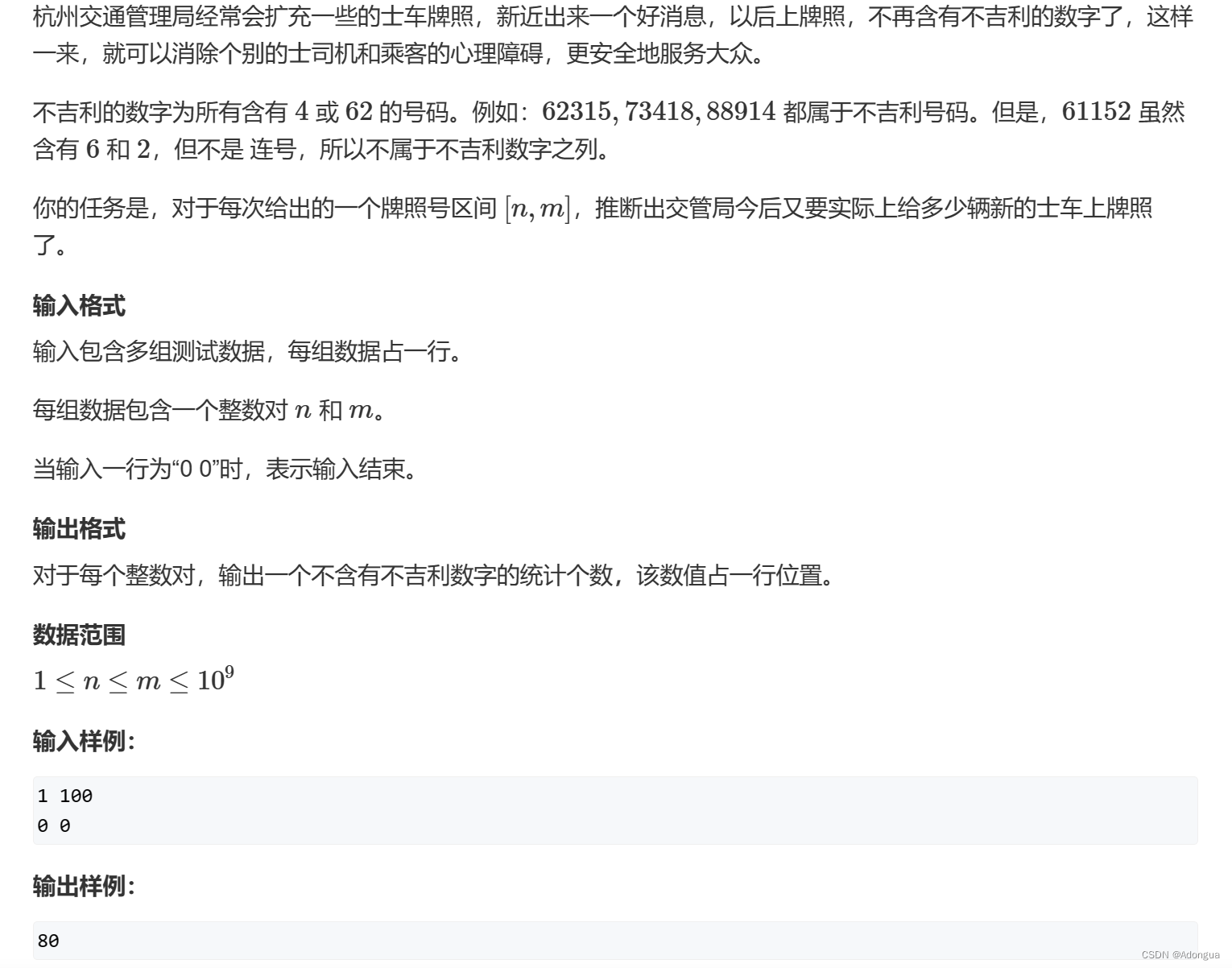
（2）代码：

#include <bits/stdc++.h>

using namespace std;

const int maxn=11;

int f[maxn][10];

void init()
{
    for(int i=0;i<=9;i++)
    {
        if(i!=4) f[1][i]=1;
    }
    for(int i=2;i<maxn;i++)
    {
        for(int j=0;j<=9;j++)
        {
            if(j==4) continue;
            for(int k=0;k<=9;k++)
            {
                if(k==4) continue;
                if(k==2&&j==6) continue;
                f[i][j]+=f[i-1][k];
            }
        }
    }
}

int dp(int n)
{
    if(!n) return 1;
    vector<int> nums;
    while(n) nums.push_back(n%10),n/=10;
    int res=0;
    int last=-1;
    for(int i=nums.size()-1;i>=0;i--)
    {
        int x=nums[i];
        for(int j=0;j<x;j++)
        {
            if(j==4) continue;
            if(j==2&&last==6) continue;
            res+=f[i+1][j];
        }
        if(x==4||x==2&&last==6) break;
        last=x;
        if(!i) res++;
    }
    return res;
}

int main()
{
    init();
    int l,r;
    while(cin>>l>>r,l&&r)
    {
        cout<<dp(r)-dp(l-1)<<endl;
    }
}

四、关于数位dp

技巧1：[X,Y] => f(Y)-f(X-1)
技巧2：树

---