目录
Trie树,即字典树,又称前缀树,是一种树形结构,典型应用是用于统计和排序大量的字符串(但不限于字符串),所以经常被搜索引擎用于文本词频统计。它的优先是,最大限度的减少无谓的字符串比较,提高查找效率。
Trie的核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销,以达到提高效率的目的
基本性质
- 根节点不包含字符,除跟节点外每个节点都只包含一个字符
- 从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串
- 每个节点的所有子节点包含的字符都不相同

实际应用,例如搜索
 #
#
208. 实现 Trie (前缀树)(medium)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。示例:
输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]解释
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True提示:
1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次

- 思路:本题这字符集长度是26,即26个小写英文字母,isEnd表示该节点是否是字符串的结尾。
- 插入字符串:从字段树的根节点开始,如果子节点存在,继续处理下一个字符,如果子节点不存在,则创建一个子节点到children的相应位置,沿着指针继续向后移动,处理下一个字符,以插入‘cad’为例
- 查找前缀:从根节点开始,子节点存在,则沿着指针继续搜索下一个子节点,直到最后一个,如果搜索到了前缀所有字符,说明字典树包含该前缀。子节点不存在就说明字典树中不包含该前缀,返回false。
- 查找字符串:和查找前缀一样,只不过最后返回的节点的isEnd是true,也就是说字符串正好是字典树的一个分支
- 复杂度分析:时间复杂度,初始化为
O(1),其余操作为O(S),s为字符串的长度。空间复杂度为O(T),T为字符集的大小,本题是26
js:
var Trie = function() {
this.children = {};
};
Trie.prototype.insert = function(word) {
let nodes = this.children;
for (const ch of word) {//循环word
if (!nodes[ch]) {//当前字符不在子节点中 则创建一个子节点到children的响应位置
nodes[ch] = {};
}
nodes = nodes[ch];//移动指针到下一个字符子节点
}
nodes.isEnd = true;//字符是否结束
};
Trie.prototype.searchPrefix = function(prefix) {
let nodes = this.children;
for (const ch of prefix) {//循环前缀
if (!nodes[ch]) {//当前字符不在子节点中 直接返回false
return false;
}
nodes = nodes[ch];//移动指针到下一个字符子节点
}
return nodes;//返回最后的节点
}
Trie.prototype.search = function(word) {
const nodes = this.searchPrefix(word);
//判断searchPrefix返回的节点是不是字符串的结尾的字符
return nodes !== undefined && nodes.isEnd !== undefined;
};
Trie.prototype.startsWith = function(prefix) {
return this.searchPrefix(prefix);
};
212. 单词搜索 II (hard)
给出一个字符串数组 words 组成的一本英语词典。返回 words 中最长的一个单词,该单词是由 words 词典中其他单词逐步添加一个字母组成。
若其中有多个可行的答案,则返回答案中字典序最小的单词。若无答案,则返回空字符串。
示例 1:
输入:words = [“w”,“wo”,“wor”,“worl”, “world”]
输出:“world”
解释: 单词"world"可由"w", “wo”, “wor”, 和 "worl"逐步添加一个字母组成。
示例 2:输入:words = [“a”, “banana”, “app”, “appl”, “ap”, “apply”, “apple”]
输出:“apple”
解释:“apply” 和 “apple” 都能由词典中的单词组成。但是 “apple” 的字典序小于 “apply”提示:
1 <= words.length <= 1000
1 <= words[i].length <= 30
所有输入的字符串 words[i] 都只包含小写字母。
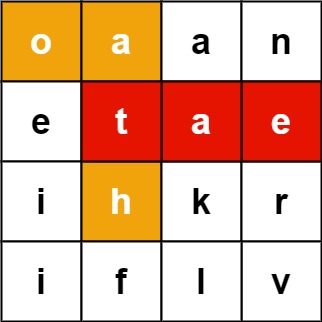
- 思路:将words数组中的所有字符串加入Trie中,然后遍历网格,判断网格路径形成的字符串在不在Trie中,然后上下左右四个方向不断回溯尝试。
- 复杂度分析:时间复杂度
O(MN⋅3^L),空间复杂度是O(max(MN, KL)),visited空间是O(MN),字典树O(KL),L是最长字符串的长度,K是words数组的长度。dfs递归栈的最大深度是O(min(L,MN)),
方法1.Trie
Js:
var findWords = function (board, words) {
const trie = new Trie();
const dxys = [
[0, -1],
[-1, 0],
[0, 1],
[1, 0],
];
const xLen = board.length,
yLen = board[0].length;
const visited = {};
const ret = [];
// 构建Trie
for (let word of words) {
trie.insert(word);
}
// DFS board
const dfs = (x, y, nodes, str) => {
if (nodes[board[x][y]].isEnd) {
ret.push(str + board[x][y]);
// 置为false是为了防止重复将字符串加入到ret中
nodes[board[x][y]].isEnd = false;
}
// 处理本层状态
nodes = nodes[board[x][y]];
str += board[x][y];
// 向四联通方向检索
visited[x * 100 + y] = true;
for (let [dx, dy] of dxys) {
const newX = x + dx,
newY = y + dy;
if (
newX < 0 ||
newY < 0 ||
newX >= xLen ||
newY >= yLen ||
!nodes[board[newX][newY]] ||
visited[newX * 100 + newY]
)
continue;
dfs(newX, newY, nodes, str);
}
visited[x * 100 + y] = false;
};
for (let x = 0; x < xLen; x++) {
for (let y = 0; y < yLen; y++) {
if (trie.children[board[x][y]]) dfs(x, y, trie.children, "");
}
}
return ret;
};
var Trie = function () {
this.children = {};
};
Trie.prototype.insert = function (word) {
let nodes = this.children;
for (const ch of word) {//循环word
if (!nodes[ch]) {//当前字符不在子节点中 则创建一个子节点到children的响应位置
nodes[ch] = {};
}
nodes = nodes[ch];//移动指针到下一个字符
}
nodes.isEnd = true;//字符是否结束
};
720. 词典中最长的单词 (easy)
给出一个字符串数组 words 组成的一本英语词典。返回 words 中最长的一个单词,该单词是由 words 词典中其他单词逐步添加一个字母组成。
若其中有多个可行的答案,则返回答案中字典序最小的单词。若无答案,则返回空字符串。
示例 1:
输入:words = [“w”,“wo”,“wor”,“worl”, “world”]
输出:“world”
解释: 单词"world"可由"w", “wo”, “wor”, 和 "worl"逐步添加一个字母组成。
示例 2:输入:words = [“a”, “banana”, “app”, “appl”, “ap”, “apply”, “apple”]
输出:“apple”
解释:“apply” 和 “apple” 都能由词典中的单词组成。但是 “apple” 的字典序小于 “apply”提示:
1 <= words.length <= 1000
1 <= words[i].length <= 30
所有输入的字符串 words[i] 都只包含小写字母。
方法1:sort+hash
- 思路:排序数组,然后遍历字符串数组,判断数组中的每个字符串的子串是否都在数组中
- 复杂度:时间复杂度
O(mn),m是字符串数组的长度,n是字符串最大长度。空间复杂度O(m)
js:
var longestWord = function (words) {
let set = new Set()
words.forEach(v => set.add(v))//set方便查找
//先按长度排序,在按字典序
words.sort((a, b) => a.length === b.length ? a.localeCompare(b) : b.length - a.length)
for (let i = 0; i < words.length; i++) {
let flag = true
for (let j = 1; j < words[i].length; j++) {
if (!set.has(words[i].substring(0, j))) {//查看set中是否有该字符串的每个子串
flag = false
break
}
}
if (flag) {
return words[i]
}
}
return ''
};
方法2:字典树
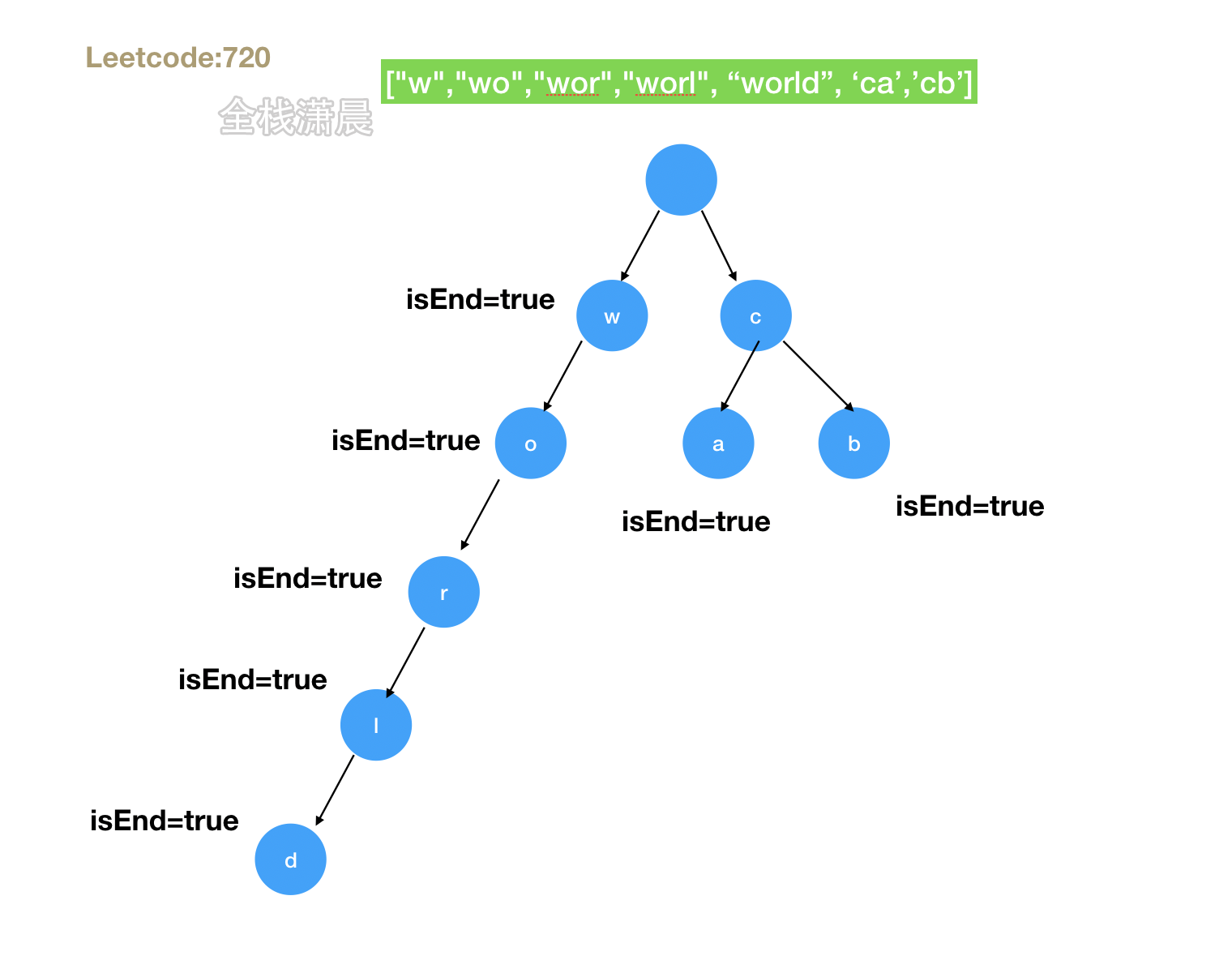
- 思路:将所有字符串插入trie中,递归寻找那个长度最大的单词
- 复杂度:时间复杂度
O(mn),m是字符串数组的长度,n是字符串最大长度。空间复杂度O(∑w)。递归深度不会超过最长单词长度,字段书的空间复杂度是所有字符串的长度和。
js:
var longestWord = function (words) {
const trie = new Trie()
words.forEach(word => {//将所有字符串插入trie中
trie.insert(word)
})
let res = ''
const _helper = (nodes, path) => {
if (path.length > res.length || (res.length === path.length && res > path)) {
res = path
}
//{a:{b1:{c1:{isEnd: true}},b2:{c2:{isEnd: true}}}}
for (const [key, value] of Object.entries(nodes)) {
if (value.isEnd) {//如果当前字符是某一个字符串的结尾
path += key
_helper(value, path)//递归寻找
path = path.slice(0, -1)//回溯
}
}
}
_helper(trie.children, '')//递归寻找那个长度最大的单词
return res
}
var Trie = function() {
this.children = {};
};
Trie.prototype.insert = function(word) {
let nodes = this.children;
for (const ch of word) {//循环word
if (!nodes[ch]) {//当前字符不在子节点中 则创建一个子节点到children的响应位置
nodes[ch] = {};
}
nodes = nodes[ch];//移动指针到下一个字符
}
nodes.isEnd = true;//字符是否结束
};
视频讲解:传送门