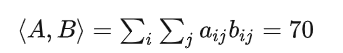在学习的过程中经常会看到蒙卡特洛和时序差分算法,到底这两个是指什么,今天稍微整理下,开始吧。
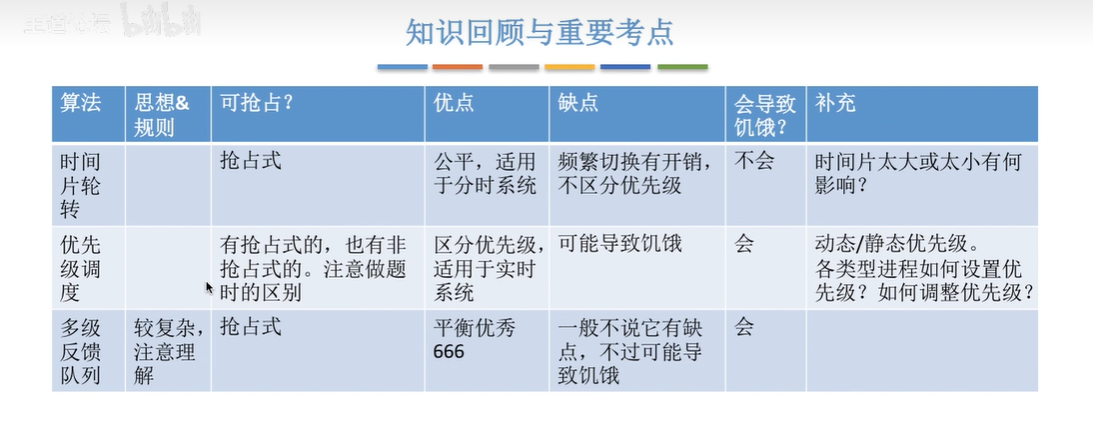
- 蒙卡特洛
1.1 蒙卡特洛方法
蒙特卡罗方法又叫做统计模拟方法,它使用随机数(或伪随机数)来解决计算问题。
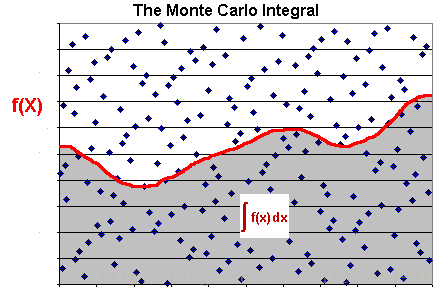
比如上图,矩形的面积我们可以轻松得到,但是对于阴影部分的面积,我们积分是比较困难的。所以为了计算阴影部分的面积,我们可以在矩形上均匀地撒豆子,然后统计在阴影部分的豆子数占总的豆子数的比例,就可以估算出阴影部分的面积了。
1.2 蒙卡特洛学习
蒙特卡罗方法的特征是采样,通过多次采样,再计算这些样本中状态的状态值的平均值,由大数定律可以知道,当样本的数目非常大时,平均值非常接近期望值。
完整的状态序列(complete episode):指从某一个状态开始,个体与环境交互直到终止状态的奖励为止.完整的状态序列不要求起始状态一定是某一个特定的状态,但是要求个体最终进入环境认可的某一个终止状态.
蒙特卡洛强化学习有如下的特点:不依赖状态转移概率(即不依赖模型),直接从经历过的完整的状态序列中学习,使用的思想就是用平均收获值代替价值.理论上完整的状态序列越多,结果越准确.
价值=平均回报
其实从字面理解就是求均值的意思。就是状态S在每一个样本中收获的回报均值。
比如,现评估某状态S的价值函数。我们采样了两个经验轨迹,从一个经验轨迹里面得到的回报是5,然后下一个经验轨迹里面的得到的回报是7,我们可以从起始状态来评估此状态的价值函数为:
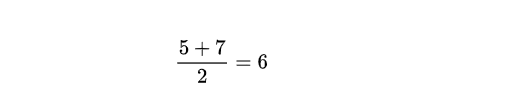
对于t时刻的状态S,未来折扣累积奖励为:
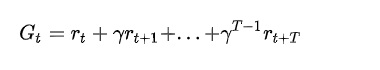
蒙特卡洛法利用经验轨迹的平均未来折扣累积奖励G作为状态值的期望。
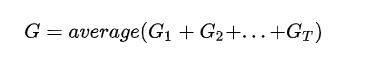
2、时序差分算法
2.1 时序差分算法
时序差分方法又称TD方法,是强化学习中应用最为广泛的一种学习方法。它结合了蒙特卡罗方法与动态规划方法,首先它可以像蒙特卡罗方法那样直接从经验中进行学习而不需要知道完整的环境模型,同时它又可以像动态规划方法那样根据已学习到的价值函数的估计进行当前估计的更新(步步更新),而不需等待整个episode结束。
2.2 时序差分公式
蒙特卡罗方法有一个缺陷,他需要在每次采样结束以后才能更新当前的值函数,但问题规模较大时,这种更新的方式显示是非常慢的。

3、总结
写了好久的草稿好像丢失了一部分,唉,无所谓了,下次还是得写好再上传
总结一下
蒙卡特洛的原理就是大数据量采样,求出平均值作为期望值,在强化学习中需要完整经过整个游戏的开始导结束,然后根据多次完整经验算出平均值
时序差分算法的原理就是根据当前和下一次的进行比较,求出期望值。
这两种算法的原理在于更新状态值的时机,一个是整个过程结束之后,一个是走一步更新一步
今天先写这些,后面会继续更新,以便更好的理解