本文是参考以下两篇文章,再结合我自己的经验完成的:
文章一:https://zhuanlan.zhihu.com/p/358417772
文章二:https://zhuanlan.zhihu.com/p/27739282
Einsum介绍:
给定矩阵A 和矩阵B (在Python中也可以说是二维数组)
我们假设:
A=
[
1
2
3
4
]
\begin{bmatrix} 1&2\\ 3&4\\\end{bmatrix}
[1324]
B=
[
5
6
7
8
]
\begin{bmatrix} 5&6\\ 7&8\\\end{bmatrix}
[5768]
用代码表示为:
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
np.einsum(‘ij’, A)返回矩阵A本身,即
np.einsum('ij', A)
Out[6]:
array([[1, 2],
[3, 4]])
np.einsum(‘ji’, A)返回矩阵A的转置(等价于:A.T),即
np.einsum('ji', A)
Out[7]:
array([[1, 3],
[2, 4]])
np.einsum(‘ii->i’, A)返回矩阵A对角线上元素的和(等价于:np.diag(A)),即
np.einsum('ii', A)
Out[9]: 5
np.einsum(‘ij->’, A)返回矩阵A所有元素之和(等价于:np.sum(A)),即
np.einsum('ij->', A) # 1+2+3+4
Out[10]: 10
np.einsum(‘ij->j’, A)返回矩阵A列向量的和(等价于:np.sum(A, axis=0)),即
np.einsum('ij->j', A)
Out[11]: array([4, 6])
np.einsum(‘ij->i’, A) 返回矩阵A行向量的和(等价于:np.sum(A, axis=1)),即
np.einsum('ij->i', A)
Out[12]: array([3, 7])
np.einsum(‘ij, ij->ij’, A, B) 是矩阵A 和矩阵B的点乘(等价于:A*B),即
np.einsum('ij, ij->ij', A, B)
Out[13]:
array([[ 5, 12],
[21, 32]])
np.einsum(‘ij, ji->ij’, A, B)是矩阵A点乘以矩阵B的转置(等价于:A*B.T),即:
np.einsum('ij, ji->ij', A, B)
Out[14]:
array([[ 5, 14],
[18, 32]])
np.einsum(‘ij, jk’, A, B) 是矩阵A乘以矩阵B —— (等价于:np.dot(A, B)),即
np.einsum('ij, jk', A, B)
Out[15]:
array([[19, 22],
[43, 50]])
np.einsum(‘ij, ij’, A, B) 是矩阵A和矩阵B 的内积
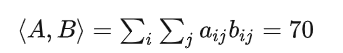
np.einsum('ij, ij', A, B)
Out[16]: 70
假设矩阵 A、B 均为二维矩阵。对于一个典型的表达式:
np.einsum('ij,jk->ik', A, B)
这个表达式被 -> 分为两部分:左边部分分别定义了两个输入矩阵的 axes(逗号分割),右边部分定义了输出矩阵的 axes。
该表达式可以对应上述部分进行理解:
- 两个输入矩阵 axes 中重复的字母表示需要沿对应 axis 进行相乘操作;
- 输出矩阵 axes 中被删掉的字母表示需要沿对应 axis 进行求和操作;
- 输出矩阵中 axes 的字母可以按任意顺序进行排列,对应输出矩阵的转置。