1 异常类型

1.1 异常值outlier

给定输入时间序列，异常值是时间戳值其中观测值与该时间序列的期望值不同。

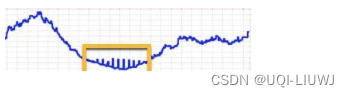
1.2 波动点（Change Point）

给定输入时间序列，波动点是指在某个时间t，其状态在这个时间序列上表现出与t前后的值不同的特性。

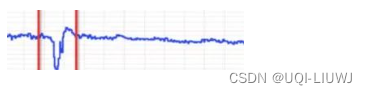
1.3 断层异常（Breakout） 

时序系统中某一时刻的值比前一时刻的值陡增或者陡降很多，之后形态也发生了改变。

2 常见异常检测方法

2.1 基于统计

• 首先建立一个数据模型。异常是那些同模型不能完美拟合的对象
  • eg，数据分布模型可以通过估计概率分布的参数来创建。如果一个对象不能很好地同该模型拟合，即如果它很可能不服从该分布，则它是一个异常

2.1.1 3σ法则

• 假如分布满足正态分布，那么  (μ−3σ,μ+3σ)区间内的概率为99.74。
• 所以可以认为，当数据分布区间超过这个区间时，即可认为是异常数据。

2.1.2 分位数异常检测

• IQR是第三四分位数减去第一四分位数，大于Q3+1.5*IQR之外的数和小于Q1-1.5*IQR的值被认为是异常值。

2.1.3  Grubbs测试

• 不断从样本中找出outlier的方法
  • 这里的outlier，是指样本中偏离平均值过远的数据

• 算法流程

  1. 样本从小到大排序

  2. 求样本的mean和std

  3. 计算此时样本的min/max与mean的差距，距离更远的那个为可疑值

  4. 求可疑值的z-score (standard score)，如果大于预先设定的Grubbs临界值，那么就是outlier；

  5. 对剩余序列不断做1~4步（每次检测一个异常点）

2.2 基于预测

• 对于单条时序数据，根据其预测出来的时序曲线和真实的数据相比，求出每个点的残差
• 对残差序列建模，利用KSigma或者分位数等方法便可以进行异常检测

2.3 基于距离

2.3.1 k-最近邻

• 数据对象与最近的k个点的距离之和。
• 很明显，与k个最近点的距离之和越小，异常分越低；与k个最近点的距离之和越大，异常分越大。
• 设定一个距离的阈值，异常分高于这个阈值，对应的数据对象就是异常点。

2.4 基于密度的方法

2.4.1 根据距离计算密度

最近k个邻居点的平均距离

2.4.2 基于邻居数量计算密度

一个数据对象的密度等于半径为d的邻域内的数据对象数

2.5 基于聚类的方法

• 小于某个最小尺寸的所有簇视为异常

参考内容：【TS技术课堂】时间序列异常检测