总结了使用Python OpenCv处理图像直方图均衡化(HE),自适应直方图均衡化(AHE),限制对比度自适应直方图均衡化(CLAHE)的方法。
目录
- 直方图均衡化(HE)
- 自适应直方图均衡化(AHE)
- 限制对比度自适应直方图均衡化(CLAHE)
- 代码
- 测试结果
- 场景1
- 场景2
直方图均衡化(HE)
HE直方图增强,大家都不陌生,是一种比较古老的对比度增强算法。
通过equalizeHist()可以实现图像的直方图均衡,它是一种全局直方图均衡,考量的对象是整幅图像。
接口形式:
cv2.equalizeHist(src[, dst]) ->dst
参数含义:
src:输入图像,8bit单通道;
dst:均衡后的输出图像,类型同src;
自适应直方图均衡化(AHE)
自适应直方图均衡化(AHE)用来提升图像的对比度的一种计算机图像处理技术。和普通的直方图均衡算法不同,AHE算法通过计算图像的局部直方图,然后重新分布亮度来改变图像对比度。因此,该算法更适合于改进图像的局部对比度以及获得更多的图像细节。缺点是有一个很大的缺陷,就是有时候会过度放大图像中相同区域的噪声。
限制对比度自适应直方图均衡化(CLAHE)
限制对比度的直方图均衡化(CLAHE)的处理方式是先为直方图设置一个阈值,该阈值为限制对比度值,超过该阈值的值会被裁剪,然后裁剪的部分会均匀的分布到其他值上,这样就重构了直方图,接下来就可以用重构后的直方图来进行接下来的均衡化操作了。
CLAHE是对比度抑制自适应直方图均衡(Contrast Limited Adaptive Histogram Equalization)的简称,不同于普通的直方图均衡,它是一种局部直方图均衡方法。
调用接口分两步,先创建实例,再调用apply()方法:
cv2.createCLAHE([, clipLimit[, tileGridSize]]) ->retval
dst=retval.apply(src)
参数含义:
clipLimit:对比对限制阈值,默认为40;
tileGridSize:直方图均衡的栅格尺寸,输入图像将会按照该尺寸分隔后进行局部直方图均衡,默认是8×8大小;
src:输入图像,8bit单通道;
dst:均衡后的输出图像,类型同src;
代码
## 直方图均衡化处理(HE),自适应直方图均衡化(AHE),限制对比度自适应直方图均衡化处理
from skimage import exposure
import cv2
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
file_to_open = './datasets/INF2Visible_Face_NoGlasses_Original/testA/(2).jpg' ## 导入图像路径
img = cv2.imread(file_to_open,cv2.IMREAD_GRAYSCALE)
print(type(img))
## 直方图均衡化处理(HE)
img_HE = cv2.equalizeHist(img)
## 自适应直方图均衡化处理(AHE)
img1 = exposure.equalize_adapthist(img)
img_AHE = Image.fromarray(np.uint8(img1 * 255))
img_AHE = np.array(img_AHE) #PIL.Image.Image转numpy.ndarry
## 限制对比度自适应直方图均衡化处理(CLAHE),也叫局部直方图均衡化处理
clahe = cv2.createCLAHE(clipLimit=2, tileGridSize=(10, 10))
img_CLAHE = clahe.apply(img) # 将灰度图像和局部直方图相关联, 把直方图均衡化应用到灰度图
plt.rcParams['font.sans-serif']=['SimHei'] #坐标图像中显示中文
plt.rcParams['axes.unicode_minus']=False
plt.figure(figsize=(20,15)) #设置大小
plt.subplot(241)
plt.imshow(img,cmap=plt.cm.gray,vmin=0,vmax=255),plt.axis("off"),plt.title("原始图像")
plt.subplot(245)
plt.hist(img.ravel(), 256), plt.title('原始图像直方图')
plt.subplot(242)
plt.imshow(img_HE,cmap=plt.cm.gray,vmin=0,vmax=255),plt.axis("off"),plt.title("直方图均衡化处理")
plt.subplot(246)
plt.hist(img_HE.ravel(), 256), plt.title('直方图均衡化处理后直方图')
plt.subplot(243)
plt.imshow(img_AHE,cmap=plt.cm.gray,vmin=0,vmax=255),plt.axis("off"),plt.title("自适应直方图均衡化处理")
plt.subplot(247)
plt.hist(img_AHE.ravel(), 256), plt.title('自适应直方图均衡化处理后直方图')
plt.subplot(244)
plt.imshow(img_CLAHE,cmap=plt.cm.gray,vmin=0,vmax=255),plt.axis("off"),plt.title("限制对比度自适应直方图均衡化处理")
plt.subplot(248)
plt.hist(img_CLAHE.ravel(), 256), plt.title('限制对比度自适应直方图均衡化处理后直方图')
plt.show()
测试结果
运行后的对比结果见下:
场景1
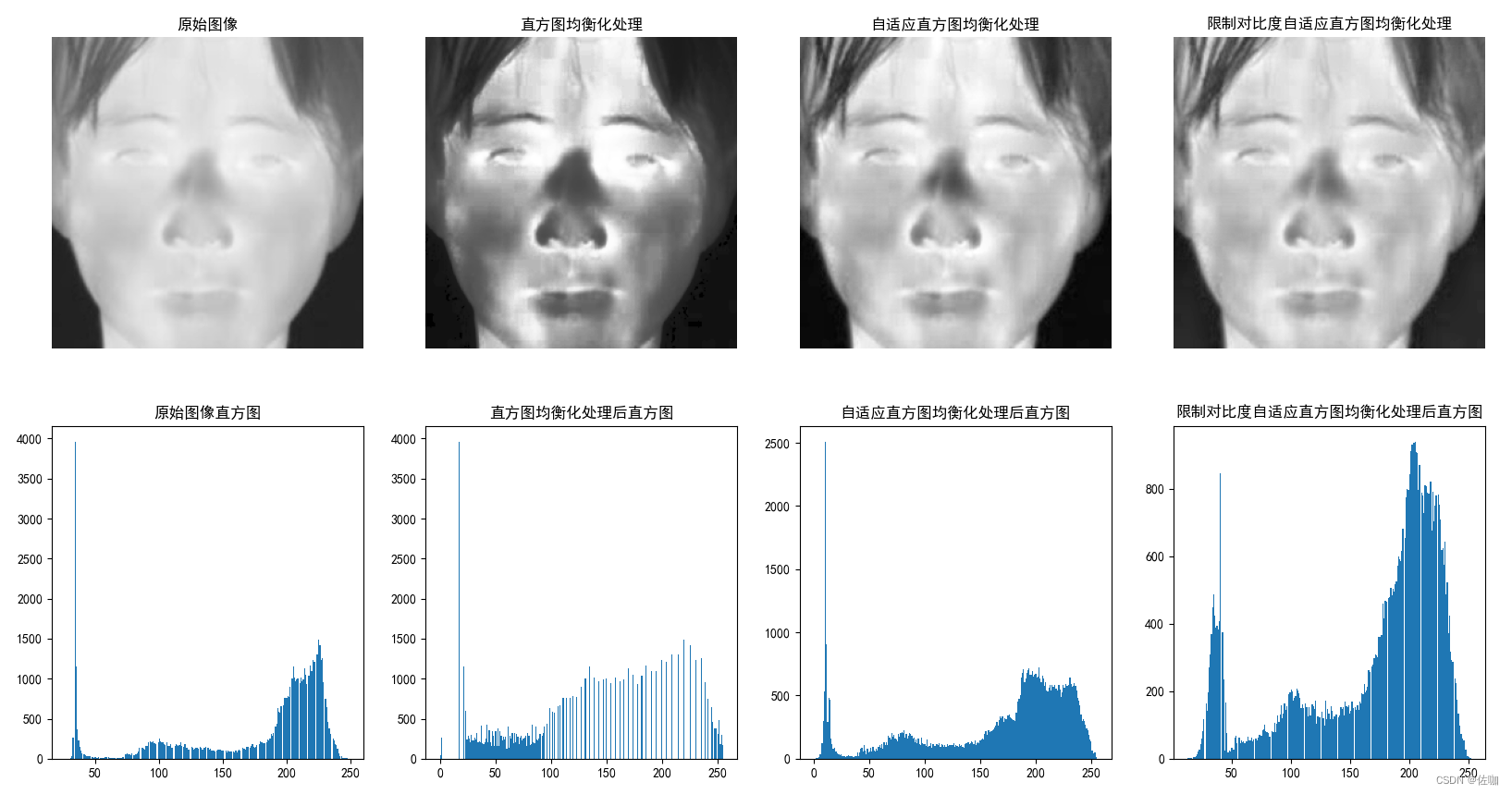
场景2
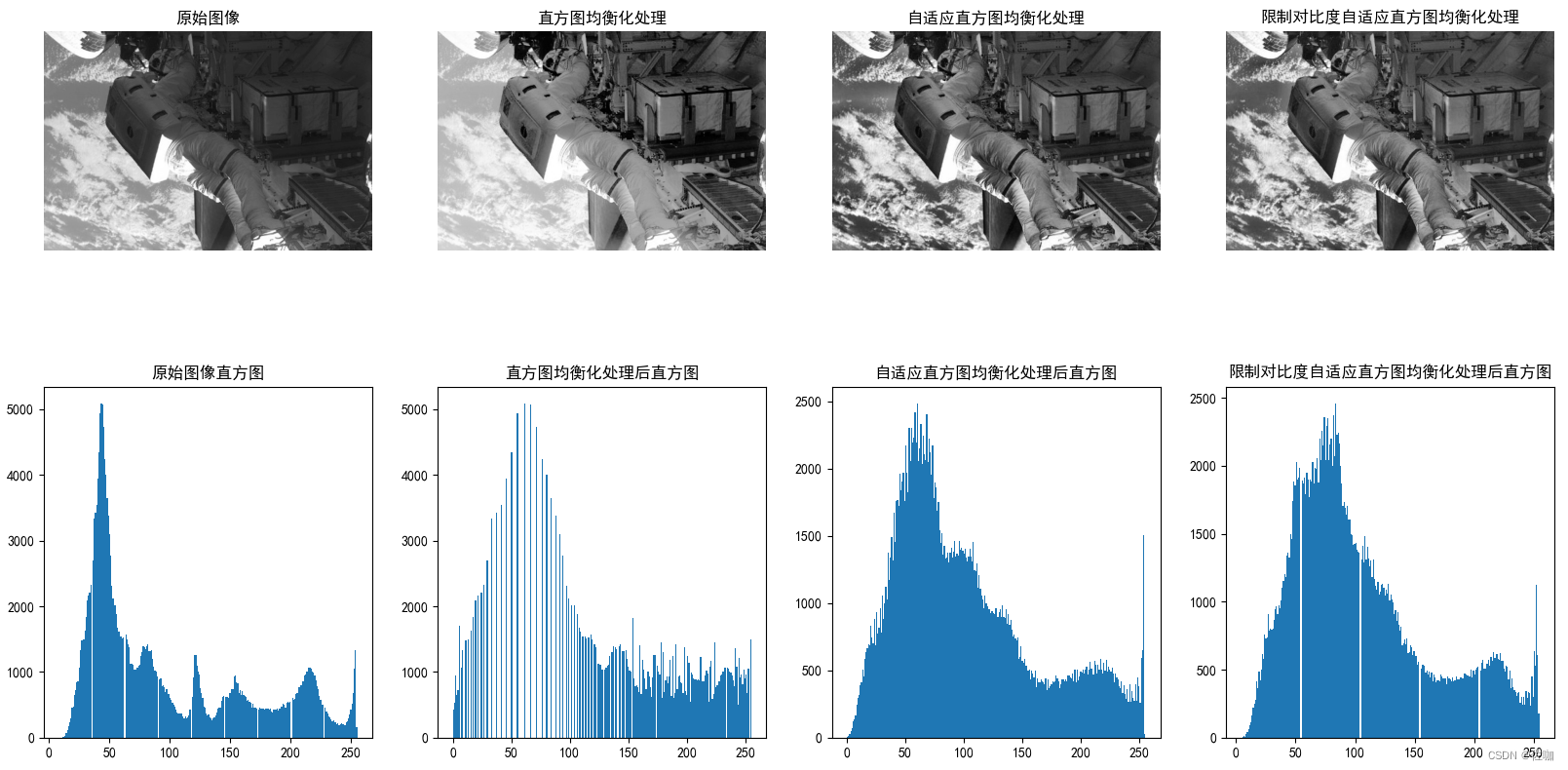
以上就是关于直方图均衡化(HE),自适应直方图均衡化(AHE),限制对比度自适应直方图均衡化(CLAHE)的代码及处理对比结果,希望能帮助到你,谢谢!