矩阵计算

矩阵计算就是讲矩阵如何求导数，所有优化模型的求解也是通过求导数实现的。

首先回忆初高中学习的导数知识，这属于标量的导数。
将导数拓展到不可微的情况，这就是亚导数。
将导数拓展到向量，这就是梯度。

向量对向量求导，就是矩阵。

搞清楚它们的形状

x，y中有一个向量的情况，求导后有两种情况：分子布局和分母布局。

分子是向量，就是分子布局，分母是向量，就要转置一下

1.x为向量

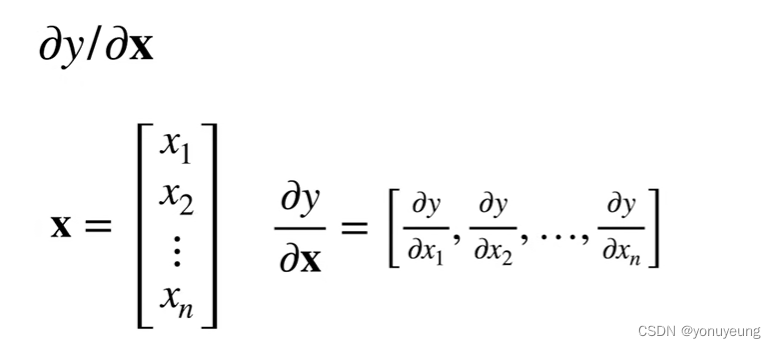
 理解：梯度就是等高线上变化最大的那个方向b

 其中的<u,v>表示内积

 

2.y为向量

3.两个都是向量

 自动求导

 自动求导有两种情况

1.对符号求导

2.对数值求导

计算原理：计算图

 自动求导分为两种模式，正向累积，反向累积

 两者对比：计算复杂度一样，但内存复杂度不同。正向累积的内存复杂度为为O(1)，反向复杂度的内存复杂度为O(n)

接下来就是实践，内容在电子书里。