质数
模板:
// 试除法判断质数
bool is_prime(int x)
{
if (x < 2) return false;
//只需枚举一部分 使得 i<= x / i, 时间复杂度为√n
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}
// 试除法分解质因数
void divide(int n)
{
for (int i = 2; i <= n / i; i++)
{
if (n % i == 0)
{
int cnt = 0;
while (n % i == 0)
{
n /= i;
cnt++;
}
printf("%d %d\n", i, cnt);
}
}
//本身就是质数
if (n > 1) printf("%d %d\n", n, 1);
printf("\n");
}
//
试除法判定质数
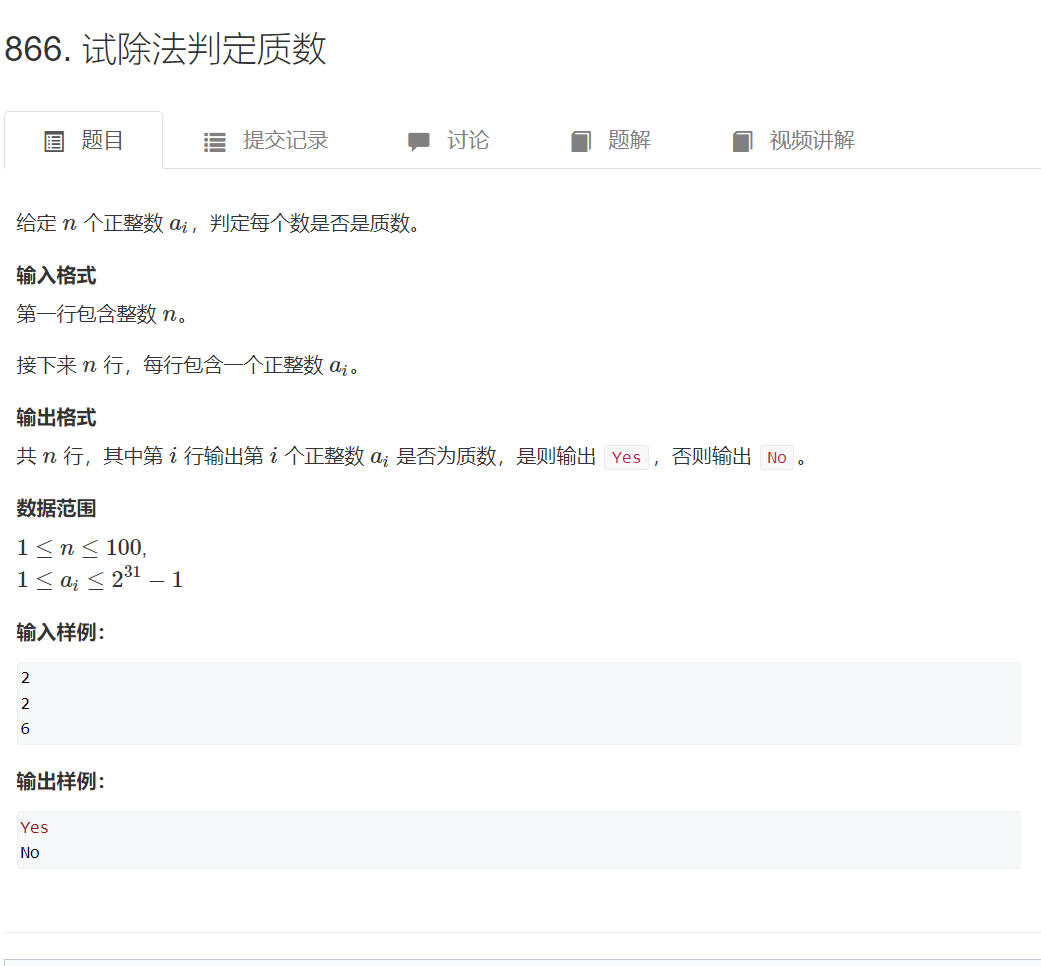
代码:
#include<iostream>
using namespace std;
int n;
bool is_prime(int x)
{
if (x == 1) return false;
for (int i = 2; i <= x / i; i++)
{
if (x % i == 0) return false;
}
return true;
}
int main()
{
scanf("%d", &n);
while (n--)
{
int a;
scanf("%d", &a);
printf(is_prime(a) ? "Yes\n" : "No\n");
}
return 0;
}
分解质因数

代码:
#include<iostream>
using namespace std;
void divide(int n)
{
for (int i = 2; i <= n / i; i++)
{
if (n % i == 0)
{
int cnt = 0;
while (n % i == 0)
{
n /= i;
cnt++;
}
printf("%d %d\n", i, cnt);
}
}
//本身就是质数
if (n > 1) printf("%d %d\n", n, 1);
printf("\n");
}
int main()
{
int n;
scanf("%d", &n);
while (n--)
{
int a;
scanf("%d", &a);
divide(a);
}
return 0;
}
筛质数
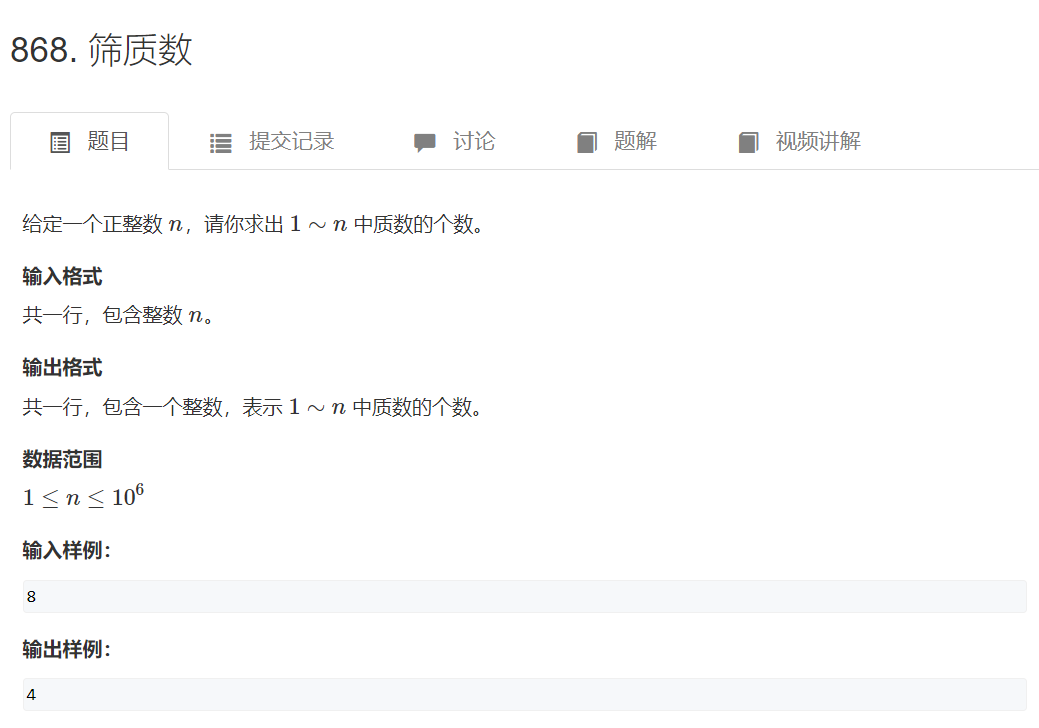
思路:
筛法求质数,有两种方式:
- 埃氏筛法
- 线性筛法
埃氏筛法
埃氏筛法每次筛掉质数的倍数(大于等于2倍),这样最后剩下的就全是质数。
s
t
[
i
]
st[i]
st[i]为
f
a
l
s
e
false
false时,表示为质数。
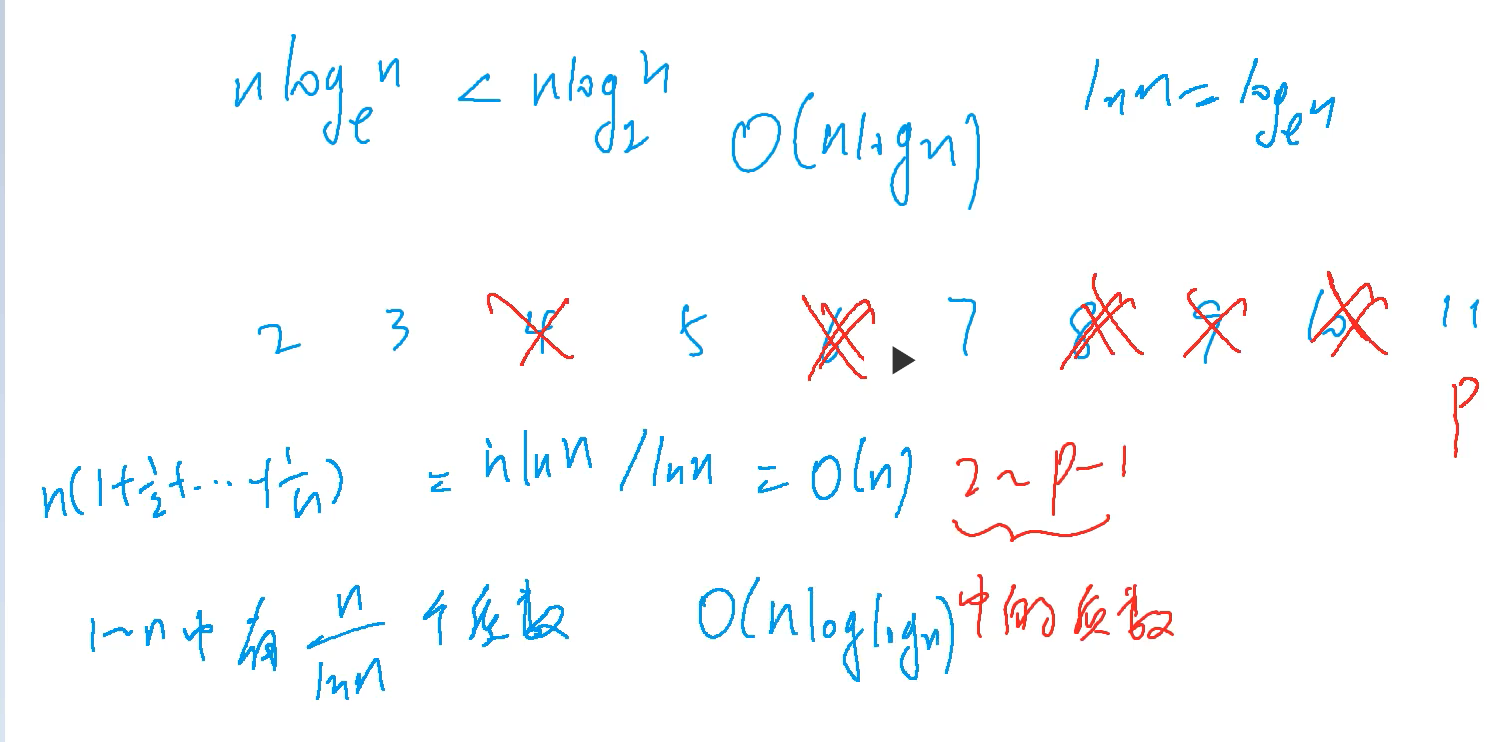
埃氏筛法代码:
#include<iostream>
using namespace std;
const int N = 1000010;
bool st[N];
int primes[N];
int cnt;
void get_primes(int n)
{
for (int i = 2; i <= n; i++)
{
if (!st[i]) primes[cnt++] = i;
for (int j = i + i; j <= n; j += i) st[j] = true;
}
}
int main()
{
int n;
cin >> n;
get_primes(n);
cout << cnt << endl;
return 0;
}
线性筛法
线性筛法保证
n
n
n只会被最小质因子筛掉。
i % primes[j] == 0,primes[j]是i的最小质因子,primes[j]是primes[j] * i的最小质因子。i % primes[j] != 0,primes[j]小于i的最小质因子,primes[j]是primes[j] * i的最小质因子。
bool st[N];
int primes[N];
int cnt;
void get_primes(int n)
{
for (int i = 2; i <= n; i++)
{
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j ++)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
线性筛法代码:
#include<iostream>
using namespace std;
const int N = 1000010;
bool st[N];
int primes[N];
int cnt;
void get_primes(int n)
{
for (int i = 2; i <= n; i++)
{
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j ++)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int main()
{
int n;
cin >> n;
get_primes(n);
cout << cnt << endl;
return 0;
}
约数
试除法求约数

代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int n;
void get_divisors(int a)
{
vector<int> res;
for (int i = 1; i <= a / i; i++)
{
if (a % i == 0)
{
res.push_back(i);
// 防止平方根多次出现
if (i != a / i) res.push_back(a / i);
}
}
//从大到小排序
sort(res.begin(), res.end());
for (int t : res) printf("%d ", t);
printf("\n");
}
int main()
{
scanf("%d", &n);
while (n--)
{
int a;
scanf("%d", &a);
get_divisors(a);
}
return 0;
}
约数个数
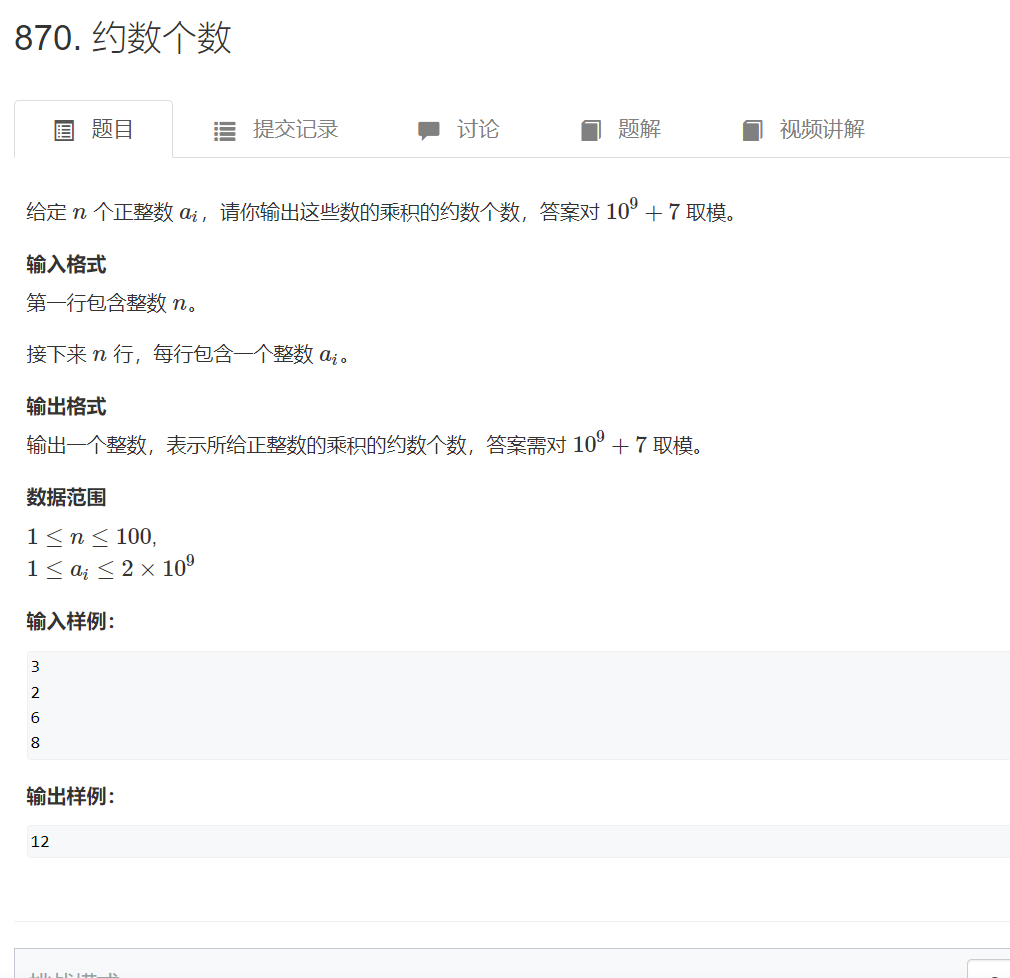
思路:
给定一个数
N
N
N,
p
i
p_i
pi为
N
N
N的质约数,则可以表示为:
N
=
p
1
α
1
×
p
2
α
2
×
p
3
α
3
×
.
.
.
×
p
k
α
k
N=p_{1}^{\alpha_1}\times p_{2}^{\alpha_2} \times p_{3}^{\alpha_3}\times... \times p_{k}^{\alpha_k}
N=p1α1×p2α2×p3α3×...×pkαk
N
N
N的每一个约数
d
i
d_i
di,可以表示为:
d
i
=
p
1
β
1
×
p
2
β
2
×
p
3
β
3
×
.
.
.
×
p
k
β
k
d_i=p_{1}^{\beta_1}\times p_{2}^{\beta_2} \times p_{3}^{\beta_3}\times... \times p_{k}^{\beta_k}
di=p1β1×p2β2×p3β3×...×pkβk
其中,
0
≤
β
i
≤
α
i
0 \le \beta_i \le \alpha_i
0≤βi≤αi,
β
i
\beta_i
βi的选法有
0
∼
α
i
0 \sim \alpha_i
0∼αi,共有
(
α
i
+
1
)
(\alpha_i + 1)
(αi+1)种选法 ,根据排列组合原理,约数个数为:
(
α
1
+
1
)
×
(
α
2
+
1
)
×
(
α
3
+
1
)
×
.
.
.
×
(
α
k
+
1
)
(\alpha_1 + 1) \times (\alpha_2 + 1) \times (\alpha_3 + 1) \times ... \times (\alpha_k + 1)
(α1+1)×(α2+1)×(α3+1)×...×(αk+1)
依次遍历
a
i
a_i
ai,求
a
i
a_i
ai的质因数以及每个质因数的个数,可以用哈希表保存结果

代码:
#include<iostream>
#include<unordered_map>
using namespace std;
const int mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
unordered_map<int, int> primes;
while (n--)
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i++)
{
while (x % i == 0)
{
x /= i;
primes[i]++;
}
}
if (x > 1) primes[x]++;
}
long long res = 1;
for (auto prime : primes)
res = res * (prime.second + 1) % mod;
cout << res << endl;
return 0;
}
约数之和
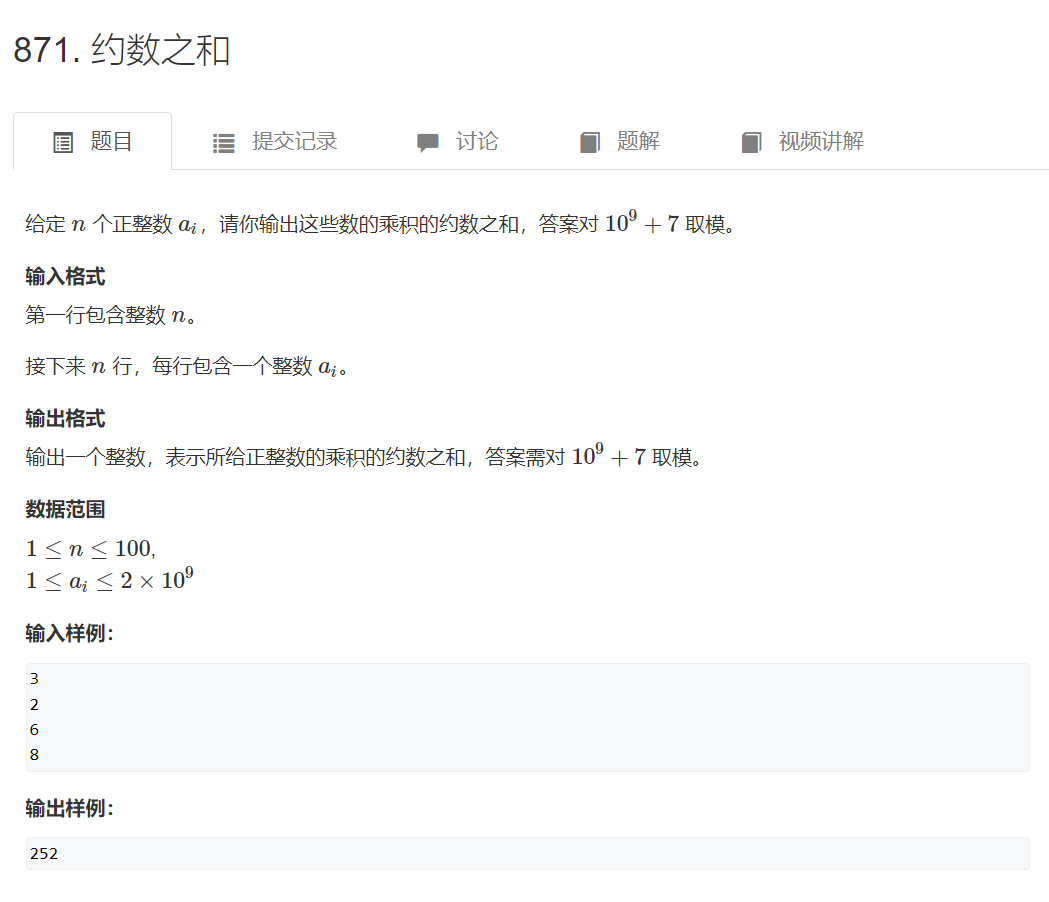
思路:
根据约数个数的思路,约数之和为
d
1
+
d
2
+
d
3
+
.
.
.
+
d
k
①
d_1 + d_2 + d_3 + ... + d_k \: \: \: ①
d1+d2+d3+...+dk①
其中,
d
i
=
p
1
β
1
×
p
2
β
2
×
p
3
β
3
×
.
.
.
×
p
k
β
k
②
d_i=p_{1}^{\beta_1}\times p_{2}^{\beta_2} \times p_{3}^{\beta_3}\times... \times p_{k}^{\beta_k} \: \: \: ②
di=p1β1×p2β2×p3β3×...×pkβk②
约数之和为
(
p
1
0
+
p
1
1
+
p
1
2
.
.
.
+
p
1
α
1
)
.
.
.
(
p
k
0
+
p
k
1
+
p
k
2
.
.
.
+
p
k
α
k
)
(p_1^0+p_1^1+p_1^2...+p_1^{\alpha_1})...(p_k^0+p_k^1+p_k^2...+p_k^{\alpha_k})
(p10+p11+p12...+p1α1)...(pk0+pk1+pk2...+pkαk)
展开可得式①,展开的每一项均为
d
i
d_i
di
(
p
i
0
+
p
i
1
+
p
i
2
.
.
.
+
p
i
α
1
)
(p_i^0+p_i^1+p_i^2...+p_i^{\alpha_1})
(pi0+pi1+pi2...+piα1)可以按照下面的方式进行推导:
t
0
=
1
t_0 = 1
t0=1
t
1
=
t
0
×
p
+
1
=
p
+
1
t_1 = t_0 \times p + 1 = p + 1
t1=t0×p+1=p+1
t
2
=
t
1
×
p
+
1
=
p
2
+
p
+
1
t_2 = t_1 \times p + 1 = p^2 + p + 1
t2=t1×p+1=p2+p+1
…
t
α
i
=
t
α
i
−
1
×
p
+
1
=
p
α
i
+
p
α
i
−
1
+
.
.
.
+
p
+
1
t_{\alpha_i }= t_{\alpha_i-1} \times p + 1 = p^{\alpha_i } + p^{\alpha_i-1} +... + p + 1
tαi=tαi−1×p+1=pαi+pαi−1+...+p+1,
最后计算
∏
i
=
1
n
t
α
i
\displaystyle\prod _{i=1}^n t_{\alpha_i}
i=1∏ntαi,即为约数之和。
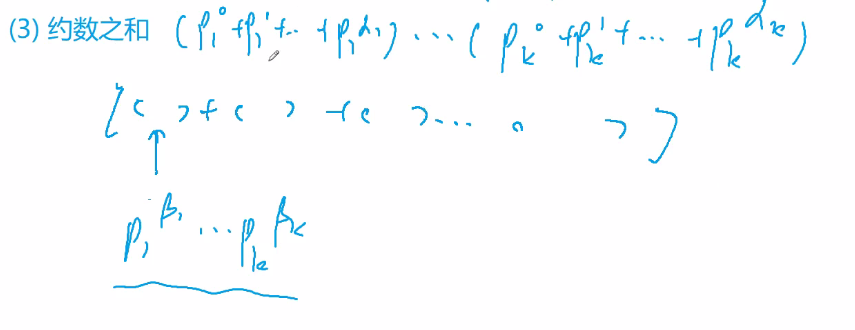
代码:
#include<iostream>
#include<unordered_map>
using namespace std;
const int mod = 1e9 + 7;
int main()
{
int n;
cin >> n;
unordered_map<int, int> primes;
while (n--)
{
int x;
cin >> x;
for (int i = 2; i <= x / i; i++)
{
while (x % i == 0)
{
x /= i;
primes[i]++;
}
}
if (x > 1) primes[x]++;
}
long long res = 1;
for (auto prime : primes)
{
long long t = 1;
int p = prime.first, a = prime.second;
while (a--) t = (t * p + 1) % mod;
res = res * t % mod;
}
cout << res << endl;
return 0;
}
最大公因数

思路:
欧几里得算法,辗转相除法。
代码:
#include<iostream>
using namespace std;
int gcd(int m, int n)
{
return m % n == 0 ? n : gcd(n, m % n);
}
int main()
{
int n;
cin >> n;
while (n--)
{
int a, b;
cin >> a >> b;
cout << gcd(a, b) << endl;
}
return 0;
}