提示：笔记内容来自于B站up主同济子豪兄

文章目录

1. Embedding嵌入的艺术
2. deepwalk
- 2.1. 什么是图嵌入？
- 2.2. deepwalk的步骤
- - 1、生成graph；
  - 2、利用random walk生成多个路径；
  - 3、训练表示向量的学习；
  - 4、为了解决分类个数过多的问题，可以利用分层softmax降低计算复杂度；
  - 5、得到每个节点的表示向量
- 2.2. deepwalk的优缺点：
- 2.3. deepwalk实战—维基百科词条嵌入可视化
- - 生成random walk
  - 训练word2vec
  - 分析word2vec的结果
  - PCA降维,可视化全部词条的二纬Embedding
  - TSNE降维可视化
3. Node2vec

1. Embedding嵌入的艺术

计算机并不认识图片、词语、节点等数据形式，但是大千万物都可以转换成向量被计算机读取和识别。embedding编码本身就是一种特征工程，是机器学习的底层逻辑。

2. deepwalk

2.1. 什么是图嵌入？

将节点表示为低维、连续、稠密的向量表示。隐式向量embedding中包含了graph中的社群、连接和结构信息，可用于后续节点分类等下游任务。

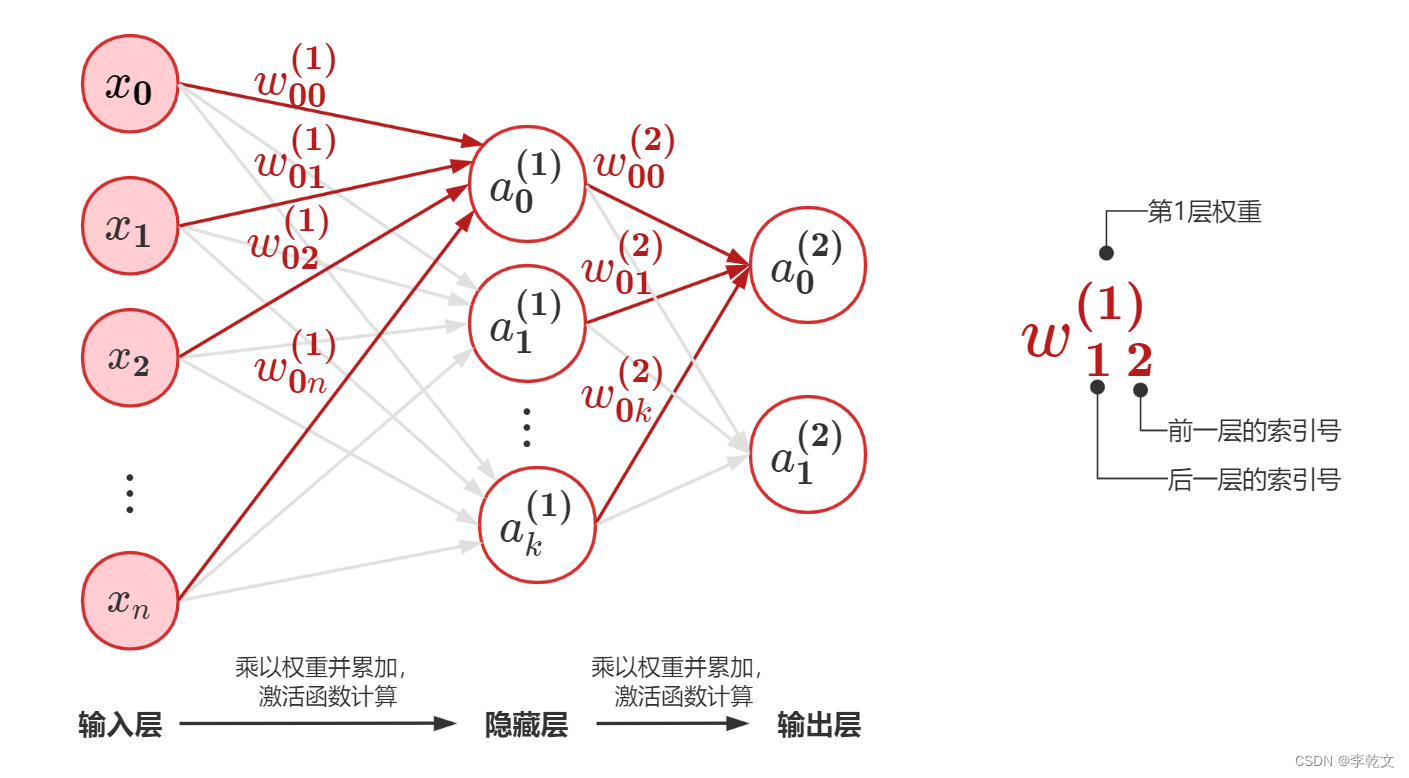
2.2. deepwalk的步骤

deep walk仿照了word2vec的思想，将随机游走形成的大量路径视作语料库，将节点本身视作单词

1、生成graph；

2、利用random walk生成多个路径；

（1）每一个节点作为起点都能产生gamma个随机游走序列；
（2）每一个随机游走的最大长度是t；
（3）完全随机的游走

3、训练表示向量的学习；

利用随机游走形成的路径walk来完成skip-gram任务

4、为了解决分类个数过多的问题，可以利用分层softmax降低计算复杂度；

霍夫曼方法将复杂度降低了，解决了分类过多导致的分母计算困难的问题。但它是工程上的技巧，对于理论研究来说并没有太多意义。

我们在模型训练的过程中需要学习两类参数：嵌入表示向量、二分类权重

5、得到每个节点的表示向量

2.2. deepwalk的优缺点：

优点：
【1】是首个将deep learning 和 NLP思想用于图机器学习的开山之作；
【2】在稀疏标注节点分类场景下，嵌入性能尤其卓越。

缺点：
【1】是均匀随机游走，没有偏向的随机游走；
【2】需要大量的随机游走序列；
【3】由于随机游走有最大长度限制，距离较远的两个节点无法相互影响，看不到全图的信息——>改进方法为图神经网络；
【4】仅仅编码了图中的连接信息，没有利用节点本身的属性特征；
【5】没有真正用到神经网络和深度学习。

2.3. deepwalk实战—维基百科词条嵌入可视化

deepwalk使用也是gensim的word2vec，所以需要下载gensim库——>pip install gensim

打开该网址
https://densitydesign.github.io/strumentalia-seealsology/
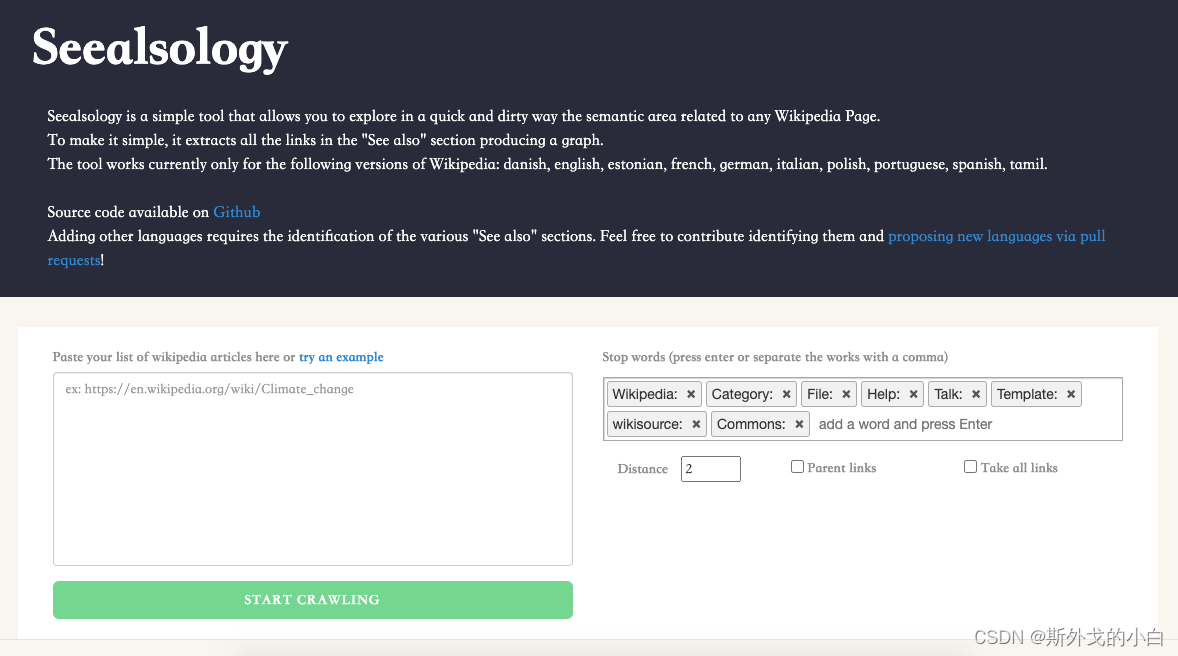
请添加图片描述
在空白窗口中输入维基百科词条网址：
https://en.wikipedia.org/wiki/Computer_vision
https://en.wikipedia.org/wiki/Deep_learning
https://en.wikipedia.org/wiki/Convolutional_neural_network
https://en.wikipedia.org/wiki/Decision_tree
https://en.wikipedia.org/wiki/Support_vector_machine

将distance设置为4

然后点击starting crawling，爬取每个词条中的sea also 以及sea also词条中的 sea also词条，获取这些词条之间的关联关系。将关联关系文档以tsv格式进行下载。

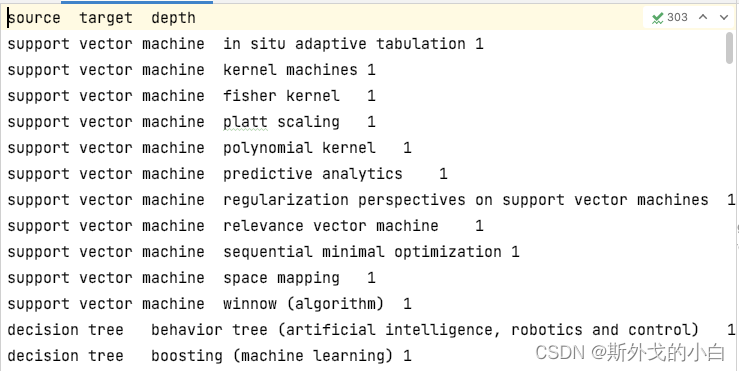
请添加图片描述
我们可以看出得到的数据集由三个字段构成，分别是起始词条和关联词条，已经它们的距离。

生成random walk

import random
import matplotlib.pyplot as plt
from tqdm import tqdm
import pandas as pd
import networkx as nx

df = pd.read_csv("seealsology-data.tsv", sep="\t")
#print(df.head())

#构建无向图
G = nx.from_pandas_edgelist(df, 'source', 'target', edge_attr=True, create_using=nx.Graph())

#print(len(G))
#2997 一共有2997个节点/词条

#如果节点个数较少的情况下，可以使用networkx自带的画图工具
'''
plt.figure(figsize=(15, 14))
nx.draw(G)
plt.show()
'''

#生成随机游走节点序列的函数
def get_random_walk(node, path_length):
    #:param node: 节点
    #:param path_length: 最大游走长度 
    #:return: 生成随机游走序列

    random_walk = [node]
    
    for i in range(path_length-1):
        #汇总邻接节点
        temp = list(G.neighbors(node))
        temp = list(set(temp)- set(random_walk))
        if len(temp) == 0:
            break
        random_node = random.choice(temp)
        random_walk.append(random_node)
        node = random_node

    return random_walk

all_nodes = list(G.nodes())
#print(all_nodes)

walk_0 = get_random_walk('random forest', 5)
print(walk_0)
#['random forest', 'decision tree', 'decision matrix']

#生成多个随机游走序列
gamma = 10
walk_length = 5

random_walks = []
for n in tqdm(all_nodes) :
    for i in range(gamma):
        random_walks.append(get_random_walk(n, walk_length))

#查看生成的随机游走的序列个数
print(len(random_walks))
#29970

print(random_walks[1])
#['support vector machine', 'winnow (algorithm)']

训练word2vec

from gensim.models import Word2Vec  #引入自然语言处理中的word2Vec

model = Word2Vec(vector_size=256,
                 window=4,
                 sg=1,#skip_gram
                 hs=0, #不加分层softmax
                 negative=10, #负采样
                 alpha=0.03, #初始学习率
                 min_alpha=0.0007, #最小学习率
                 seed=14) #随机数种子

#用随机游走序列构建词汇表
model.build_vocab(random_walks, progress_per=2)
#训练
model.train(random_walks, total_examples=model.corpus_count, epochs=50, report_delay=1)

分析word2vec的结果

#查看某个节点的Embedding
print(model.wv.get_vector('random forest').shape)
#(256,)

print(model.wv.get_vector('random forest'))
‘’‘
[-1.75103508e-02  1.50574550e-01 -2.90710241e-01  1.76696718e-01
 -5.17038740e-02  1.66850671e-01  1.79646611e-01 -1.85463339e-01
  2.81677216e-01 -5.35606481e-02  4.59016144e-01 -1.76348865e-01
 -3.28859121e-01 -3.44423443e-01  3.75596583e-01 -4.68409240e-01
 -2.21335828e-01 -8.15981552e-02 -5.54344878e-02  1.30867675e-01
  1.55458391e-01  1.29232155e-02 -2.52916038e-01 -1.31590432e-02
  2.55613446e-01  8.24676678e-02  1.85618207e-01  1.00504821e-02
 -2.72096366e-01  1.40075818e-01  2.95037150e-01  2.61273235e-01
 -4.44846228e-02 -2.92456634e-02  6.46213517e-02 -1.12667993e-01
 -1.53965667e-01 -8.84412304e-02  6.18105829e-01 -3.26152682e-01
 -7.80166537e-02  5.80004513e-01  2.01196656e-01  8.16753954e-02
 -2.23055497e-01 -2.27746129e-01  3.98028016e-01 -1.62307441e-01
 -1.67772509e-02  2.06478521e-01  4.63583171e-01  1.65199265e-02
 -8.56528282e-02 -2.71654159e-01 -3.90159607e-01  9.95318145e-02
  1.55404046e-01 -1.40964076e-01 -2.39251673e-01  1.21304125e-01
 -3.94109078e-02  2.59401202e-01  8.35981146e-02 -4.90658224e-01
  2.82326825e-02  2.53487706e-01  1.26222789e-01 -1.99732661e-01
  1.94451108e-03 -2.28737921e-01  3.43216419e-01 -5.53002842e-02
  1.63973257e-01 -6.29538059e-01  3.20530862e-01  8.56027603e-02
  3.51878405e-02  5.39098084e-01  1.35973588e-01  7.30506778e-02
  3.19665611e-01  2.77461708e-01  2.96689216e-02 -2.11343706e-01
  2.84282267e-01  8.14686567e-02  2.45499462e-01 -1.42508209e-01
 -4.14810121e-01 -8.04831460e-03 -3.19779605e-01  2.68085748e-01
  2.22785279e-01  2.71854669e-01 -6.96179420e-02 -3.18581313e-01
  3.31286364e-03 -5.47539890e-01  2.84994304e-01  3.93303663e-01
  1.91131711e-01 -2.16357216e-01 -1.56001657e-01 -3.35288137e-01
  4.12162870e-01  9.77841914e-02 -2.24288866e-01 -6.24972731e-02
  3.64813268e-01  9.10555050e-02  1.95117980e-01 -1.95311293e-01
  1.18188366e-01  1.83854178e-01 -2.61452228e-01 -1.24820471e-02
  1.61693364e-01  9.24856067e-02 -4.67351861e-02 -8.72675478e-02
 -4.82643098e-01  5.97176015e-01  4.24284711e-02 -2.02761844e-01
 -3.07757556e-01  3.87791425e-01 -5.26242077e-01  4.10861760e-01
 -1.78288743e-01  3.61336907e-03  3.40764612e-01  1.26055405e-01
 -3.41932595e-01  2.90207148e-01  7.49768764e-02  6.12589240e-01
 -2.30110154e-01  2.91005284e-01  1.64296106e-01  1.63664743e-01
 -3.36904377e-02  5.05201111e-04 -1.53249636e-01  3.09505701e-01
  3.74861270e-01 -2.91956455e-01 -5.25003448e-02  2.80535370e-01
 -4.94016886e-01 -2.68832207e-01 -7.23569393e-02 -2.25934073e-01
 -3.64224106e-01 -2.58031249e-01 -2.07863286e-01 -2.33434975e-01
  3.68695892e-02 -2.20692620e-01  2.77577549e-01  3.77851516e-01
 -1.24636807e-01  3.15518856e-01 -4.37836861e-05 -3.39763701e-01
 -2.16543704e-01 -2.76362449e-01 -8.93585235e-02  2.83290803e-01
 -1.18302461e-02 -2.74810851e-01  1.69479419e-02  1.82554409e-01
 -7.05644414e-02 -1.63607836e-01 -2.97632009e-01 -1.45971522e-01
  1.29671618e-01 -1.35711581e-01  1.68824159e-02  2.62595803e-01
 -2.19873369e-01  3.56505692e-01  1.82276666e-01  7.54332319e-02
  5.89607179e-01 -1.08422928e-01  4.02044922e-01  6.78051114e-02
  4.46608849e-02 -2.23213509e-01 -1.72709554e-01  1.54766485e-01
  1.22157723e-01 -4.35440242e-01  1.56108603e-01  1.18483208e-01
 -2.12001026e-01  3.47642392e-01  7.51201436e-02  1.17612652e-01
  4.28414494e-01 -1.85382769e-01 -1.99222997e-01  8.91974568e-02
  2.46173590e-01  4.84630734e-01 -7.81275681e-04 -1.42655149e-01
  1.67864487e-02  1.50540844e-01 -1.49479121e-01  1.20230183e-01
 -1.27135783e-01  2.56091475e-01 -1.98269784e-01 -1.22426338e-01
 -1.27900615e-01 -9.82931405e-02  6.70286059e-01  9.26854983e-02
 -3.86442572e-01  1.68649212e-01  3.18761051e-01 -3.86268467e-01
  1.57067440e-02  2.63682276e-01  4.72340614e-01 -1.13149583e-01
  1.74417928e-01 -3.13653380e-01  1.18547402e-01 -1.27085624e-02
  3.82784121e-02  2.20095113e-01 -1.46961883e-01  2.85839438e-01
  1.10681936e-01 -6.00838177e-02  1.18011311e-01  2.23752394e-01
 -4.71865311e-02  3.00609976e-01 -1.20546453e-01  5.50452769e-01
 -3.06917340e-01  4.45183933e-01  2.02446222e-01 -4.10432033e-02
  2.52888292e-01  2.75853984e-02  3.23300451e-01  3.27498317e-01
 -2.01862916e-01 -1.61864311e-01  3.87831748e-01  3.19291502e-01]
’‘’

#找相似的词语
a = model.wv.similar_by_word('random forest')
print(a)
‘’‘
[('ordinal priority approach', 0.9988303184509277), ('decision tree model', 0.9963210225105286), ('topological combinatorics', 0.9958150386810303), ('drakon', 0.9931159019470215), ('truth table', 0.992505669593811), ('boosting (machine learning)', 0.9916960000991821), ('decision matrix', 0.9916875958442688), ('decision list', 0.991100013256073), ('markov chain', 0.9860553741455078), ('behavior tree (artificial intelligence, robotics and control)', 0.9833813905715942)]
’‘’

PCA降维,可视化全部词条的二纬Embedding

X = model.wv.vectors
#将embedding用PCA降维到2维
from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=420)
embed_2d = pca.fit_transform(X)
print(embed_2d.shape)

plt.figure(figsize=(14, 14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.savefig("pca_2d_visualization.png")
plt.show()

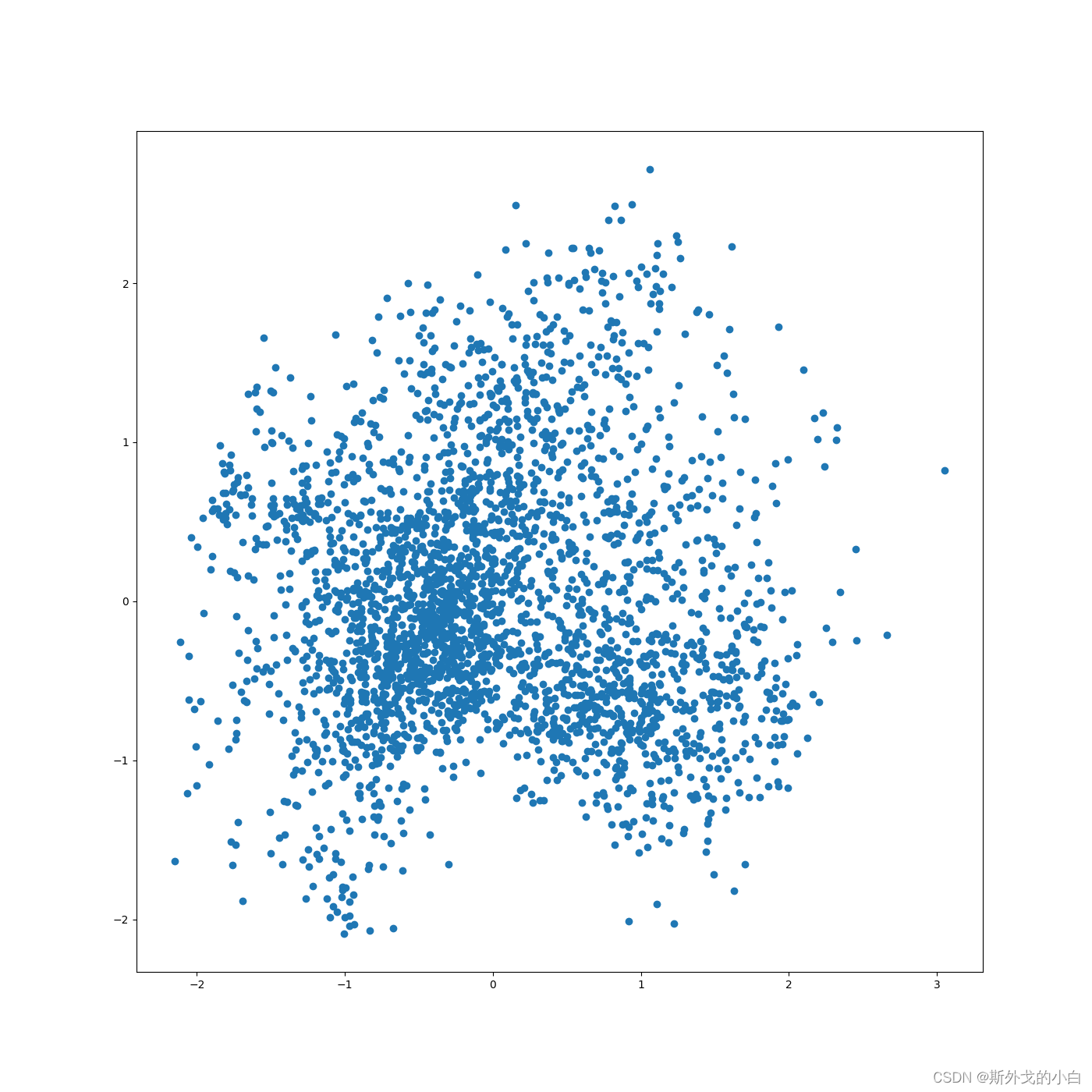
请添加图片描述

可视化某个词条的embedding

term = 'computer vision'
term_256d = model.wv[term].reshape(1, -1)
print(term_256d.shape)
term_2d = pca.transform(term_256d)
print(term_2d)
#[[-0.5167788   0.98488086]]

plt.figure(figsize=(14, 14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.scatter(term_2d[:, 0], term_2d[:, 1], c='r', s=400)
plt.savefig("term_computer_vision_2d.png")
plt.show()

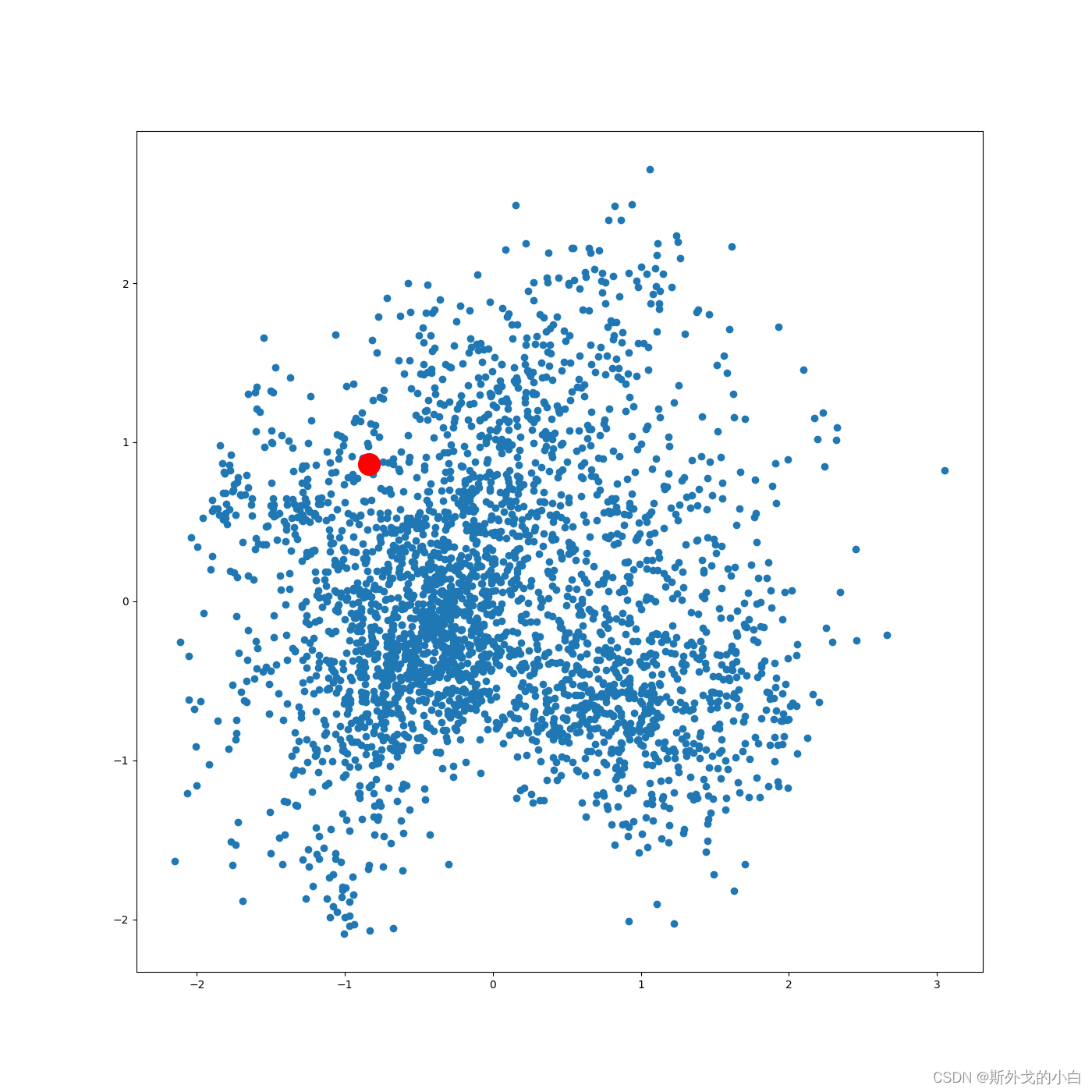
请添加图片描述

可视化某些词条的二维Embedding
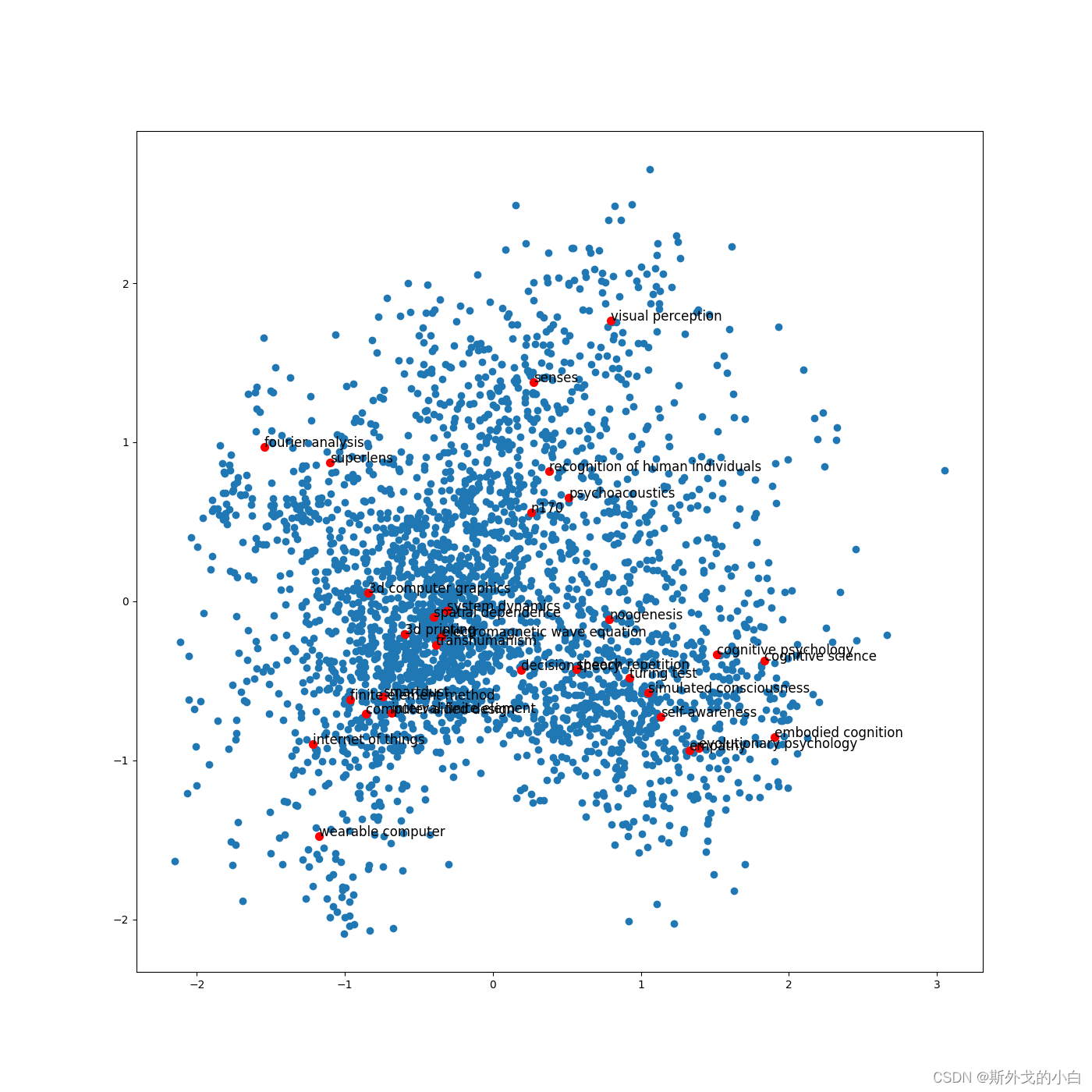
计算PageRank的重要成都

pagerank = nx.pagerank(G)
#从高到底排序
node_important = sorted(pagerank.items(), key=lambda x:x[1], reverse=True)
#取最高的前n个节点
n = 30
terms_choosen = []
for each in node_important[: n]:
    terms_choosen.append(each[0])

print(terms_choosen)


#输入词条，输出词典中的索引号
term2index = model.wv.key_to_index
plt.figure(figsize=(14, 14))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])

for item in terms_choosen:
    idx = term2index[item]
    plt.scatter(embed_2d[idx, 0], embed_2d[idx, 1], c='r', s=50)
    plt.annotate(item, xy=(embed_2d[idx, 0], embed_2d[idx, 1]), c='k', fontsize=12)
plt.savefig("page_rank.png")
plt.show()

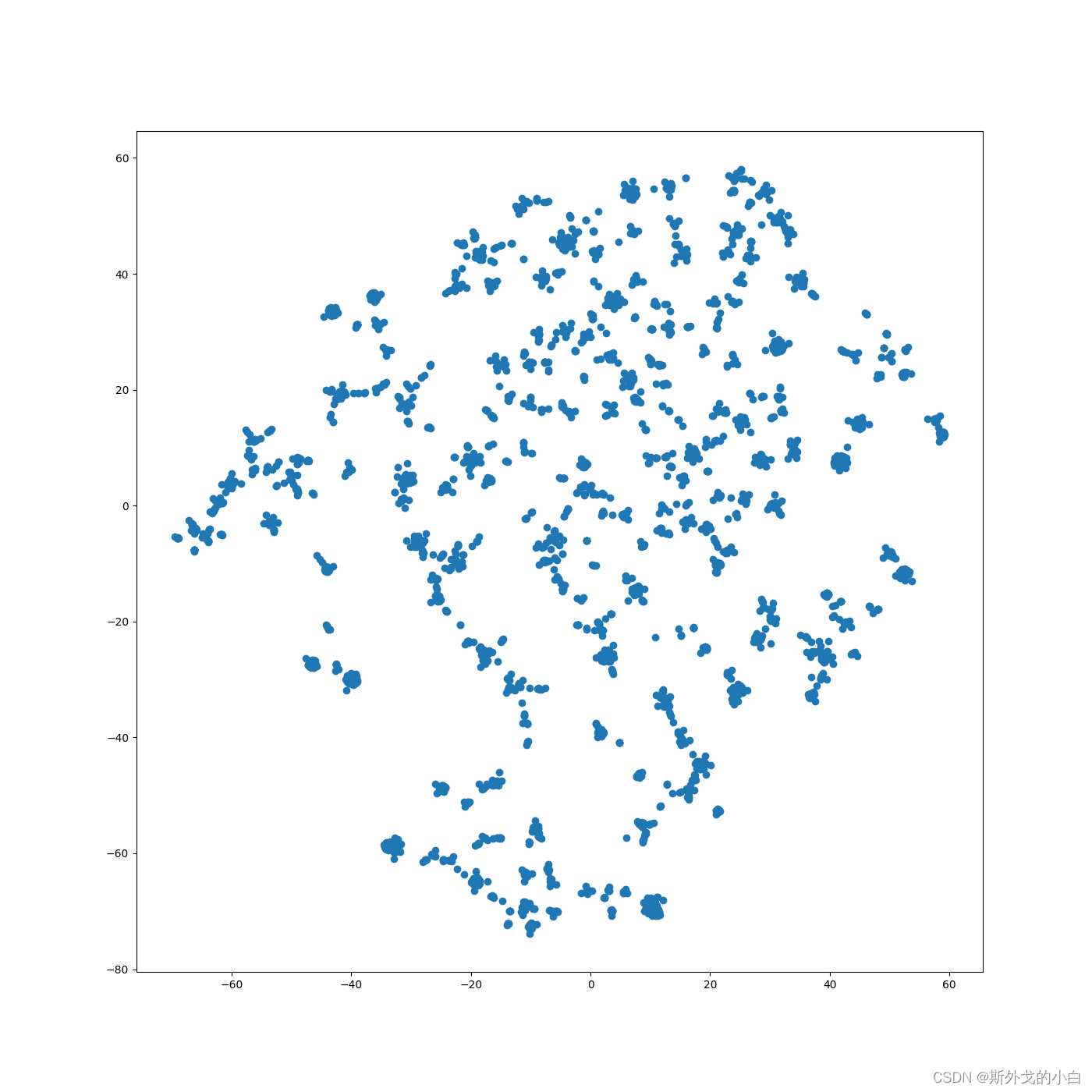
请添加图片描述

TSNE降维可视化

from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, n_iter=1000, random_state=430)
emd_2d_new = tsne.fit_transform(X)
plt.figure(figsize=(14, 14))
plt.scatter(emd_2d_new[:, 0], emd_2d_new[:, 1])
plt.savefig('TSNE.png')
plt.show()




plt.figure(figsize=(14, 14))
plt.scatter(emd_2d_new[:, 0], emd_2d_new[:, 1])

for item in terms_choosen:
    idx = term2index[item]
    plt.scatter(emd_2d_new[idx, 0], emd_2d_new[idx, 1], c='r', s=50)
    plt.annotate(item, xy=(emd_2d_new[idx, 0], emd_2d_new[idx, 1]), c='k', fontsize=12)
plt.savefig("page_rank_tsne.png")
plt.show()

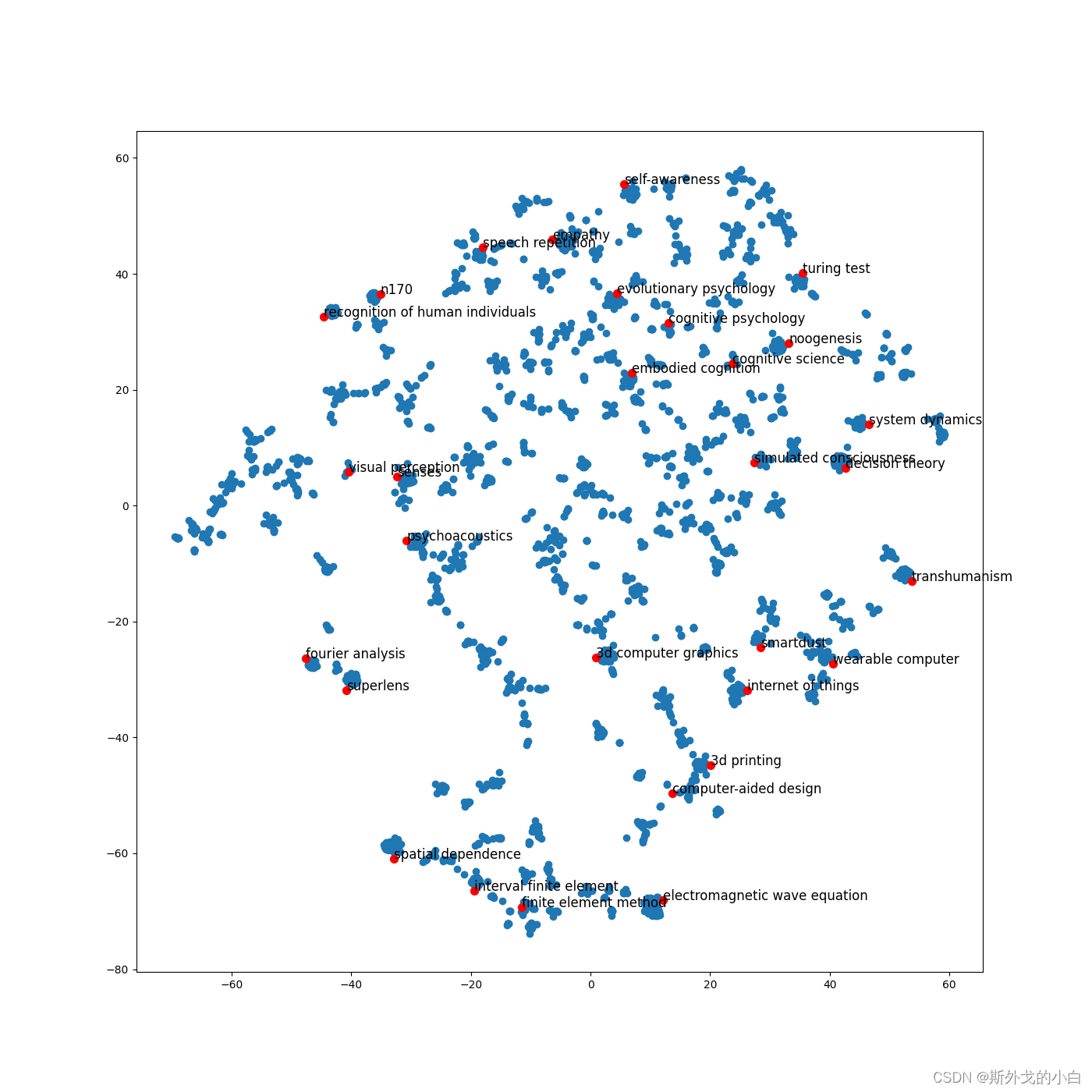
请添加图片描述

3. Node2vec

deepwalk的缺点：用完全随机游走训练节点嵌入向量，学习得到的表示向量仅能反映相邻节点的社群相似信息，无法反映节点的功能角色相似信息。
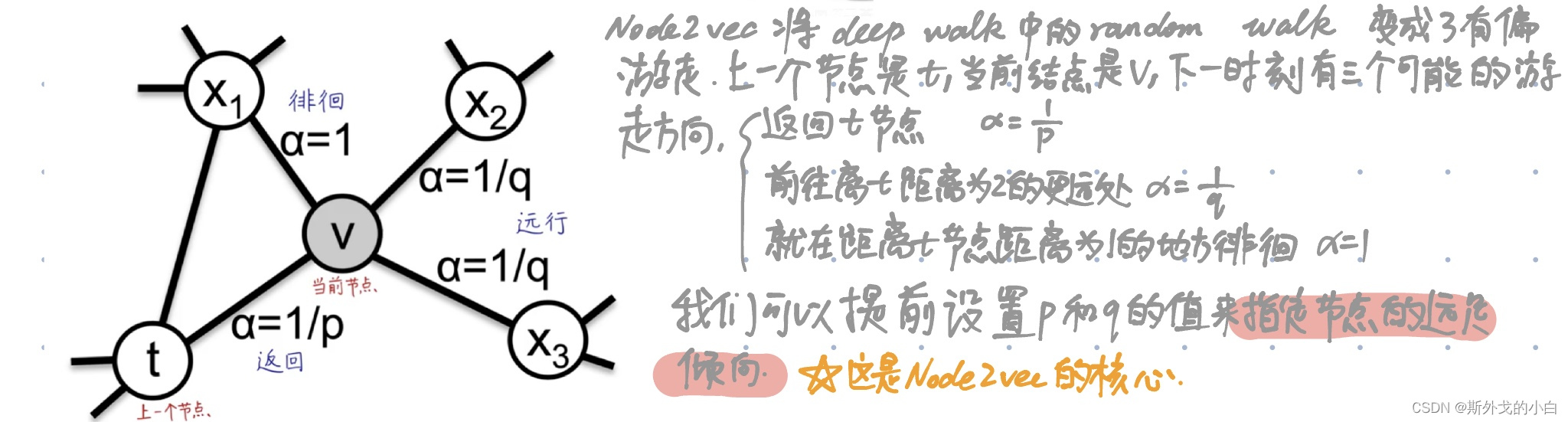
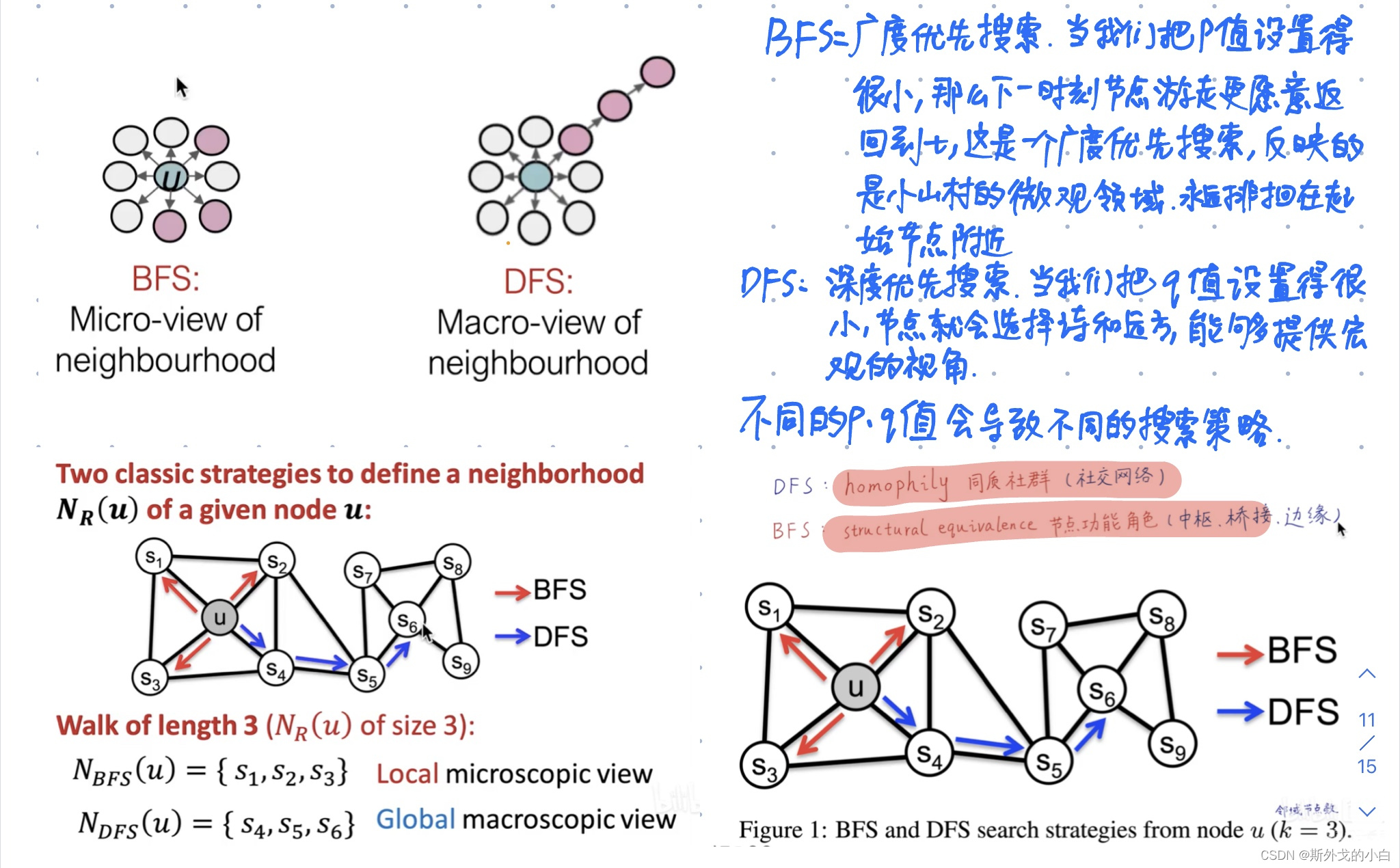
请添加图片描述

Node2vec叫做二阶随机游走，也叫二阶马尔科夫，下一个节点走向哪里，不仅取决于当前节点，还取决于上一个节点。

Node2vec图嵌入算法在deep walk完全随机游走的基础上，增加了p/q参数，实现有偏随机游走。不同的p和q的组合，对应了不同的探索范围和节点语义。当p和q等于1的时候，node2vec就是deepwalk的一个特例。
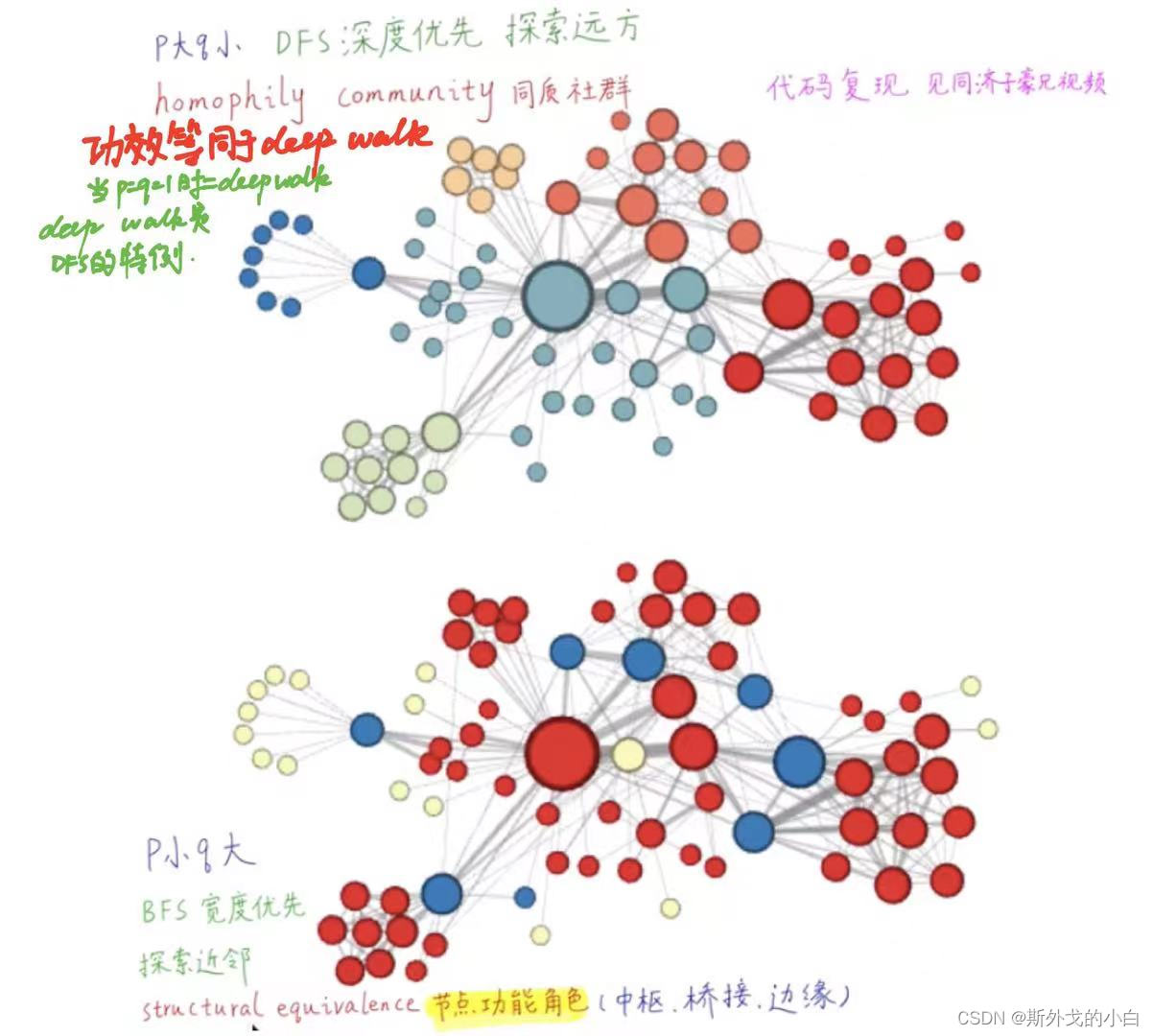
请添加图片描述
缺点：需要有大量的游走序列训练；距离较远的两个节点无法直接互相影响，看不到全图的特征；仅编码图的连接信息，没有利用节点的属性特征；没有真正运用到神经网络和深度学习。

代码实战，复现论文中的经典插图：
pip install node2vec

from node2vec import Node2Vec
import networkx as nx
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt


#倒入数据集
#《悲惨世界》人物数据集
G = nx.les_miserables_graph()
print(G.nodes)
print(len(G))


#可视化
plt.figure(figsize=(14, 15))
pos = nx.spring_layout(G, seed=3)
nx.draw(G, pos, with_labels=True)
plt.savefig('les_miserables_graph.png') 
plt.show()

在这里插入图片描述

#设置node2vec参数
node2vec_ = Node2Vec(G,
                    dimensions=32, #嵌入向量维度
                    p=1, #回家参数
                    q=3, #外出参数
                    walk_length=10, #随机游走最大长度
                    num_walks=600, #每个节点作为起始点生成的随机游走路径数
                    workers=4 #并行线程数
                    )

# p=1, q=0.5, n_clusters=6。DFS深度优先搜索，挖掘同质社群
# p=1, q=2, n_clusters=3。BFS宽度优先搜索，挖掘节点的结构功能。

#训练Node2vec,参考文档见 gensim.models.Word2Vec
model = node2vec_.fit(window=3,  #skip-gram窗口大小
                      min_count=1, #忽略出现次数低于次数的节点，设置阈值
                      batch_words=4 #每个线程处理的数据量
                      )
#print('finish')
X = model.wv.vectors
print(X.shape)
#(77, 32)

#(77, 32)


#查看Embedding
shape_ = model.wv.get_vector('Napoleon').shape
print(shape_)
#(32,)

#查看某个节点的embedding
embedding_ = model.wv.get_vector('Napoleon')
print(embedding_)
'''
[-0.54533213 -0.26237386  0.760342   -0.80337083 -0.33498412 -0.82809657
  0.627769    0.80122554 -0.16920353  0.02333984 -0.02064326 -0.18039408
 -0.01096789  0.16308258  0.02162968 -0.30133647 -0.23102102  0.48328704
  0.14346716  0.00538726 -0.05620801  0.37786493  0.9842375  -0.5410597
 -0.09757584  0.03198021 -0.21530095  0.6917203   0.41528413 -0.3989606
 -0.12605394  0.21376027]
'''
#查找Napoleon节点的相似节点
similar_ = model.wv.most_similar('Napoleon')
print(similar_)
#[('Cravatte', 0.9765666723251343), ('Geborand', 0.9585205912590027), ('OldMan', 0.957446813583374), ('CountessDeLo', 0.9490584135055542), ('Count', 0.9405924081802368), ('Champtercier', 0.9149487018585205), ('MlleBaptistine', 0.9055278301239014), ('MmeMagloire', 0.8933127522468567), ('Myriel', 0.872755229473114), ('Valjean', 0.4431787133216858)]


similar_1 = model.wv.similar_by_word('Napoleon')
print(similar_1)
#[('Cravatte', 0.9765666723251343), ('Geborand', 0.9585205912590027), ('OldMan', 0.957446813583374), ('CountessDeLo', 0.9490584135055542), ('Count', 0.9405924081802368), ('Champtercier', 0.9149487018585205), ('MlleBaptistine', 0.9055278301239014), ('MmeMagloire', 0.8933127522468567), ('Myriel', 0.872755229473114), ('Valjean', 0.4431787133216858)]


#查看任意两个节点的相似度
pair_similarity = model.wv.similarity('Napoleon', 'Champtercier')
print(pair_similarity)
#0.9149486

对Edge（连接）做Embedding

from node2vec.edges import HadamardEmbedder
# Hadamard 二元操作符：两个 Embedding 对应元素相乘
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)

# 查看 任意两个节点连接 的 Embedding
edges_embedding = edges_embs[('Napoleon', 'Champtercier')]
print(edges_embedding)

'''
[ 1.19825505e-01 -4.14662249e-03  6.86520875e-01  4.44835037e-01
  1.58184484e-01  3.99384886e-01  5.11850655e-01  6.89081967e-01
  5.50679006e-02  5.00345230e-03 -1.08206156e-03  1.74393076e-02
 -2.33720313e-03  3.81250829e-02  4.17734589e-03  4.93945293e-02
 -1.15864035e-02  1.77816108e-01  2.74095591e-02  4.30415297e-04
  2.46398021e-02  2.61548758e-01  9.83004034e-01  1.83459595e-01
  2.87434906e-02 -1.15166919e-03  5.54209165e-02  5.12513161e-01
  1.87654138e-01  1.29544646e-01  3.29113565e-02  6.38123378e-02]
'''


# 计算所有 Edge 的 Embedding
edges_kv = edges_embs.as_keyed_vectors()
print(edges_kv.index_to_key)


# 查看关系与某两个节点最相似的节点对
edges_pair_similar = edges_kv.most_similar(str(('Bossuet', 'Valjean')))
print(edges_pair_similar)
[("('Enjolras', 'Valjean')", 0.947335422039032), ("('Bahorel', 'Valjean')", 0.9243528842926025), ("('Joly', 'Valjean')", 0.9180840849876404), ("('Prouvaire', 'Valjean')", 0.8983640670776367), ("('Combeferre', 'Valjean')", 0.8965768814086914), ("('Feuilly', 'Valjean')", 0.8657184839248657), ("('Courfeyrac', 'Valjean')", 0.865365207195282), ("('Grantaire', 'Valjean')", 0.774030864238739), ("('MmeHucheloup', 'Valjean')", 0.7463048100471497), ("('Joly', 'MmeThenardier')", 0.7413285970687866)]

节点Embedding聚类可视化

from sklearn.cluster import KMeans

clusters_labels = KMeans(n_clusters=3, random_state=12).fit(X).labels_
print(clusters_labels)


colors = []
nodes = list(G.nodes)
for node in nodes: # 按 networkx 的顺序遍历每个节点
    idx = model.wv.key_to_index[str(node)] # 获取这个节点在 embedding 中的索引号
    colors.append(clusters_labels[idx]) # 获取这个节点的聚类结果


#可视化聚类效果
plt.figure(figsize=(15, 14))
pos = nx.spring_layout(G, seed=10)
nx.draw(G, pos, node_color=colors, with_labels=True)
plt.savefig('cluster.png')
plt.show()

在这里插入图片描述
节点Embedding降维可视化

from sklearn.decomposition import PCA
pca = PCA(n_components=2, random_state=2)
embed_2d = pca.fit_transform(X)

plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.savefig('decomposition.png')
plt.show()