一、前言

前面介绍了《感知器》，类似于单个神经元细胞，现在我们用多个感知器组合成更加复杂的神经网络。本文介绍了多层神经网络通过前向传播方法，逐层计算出最终结果值的过程。

二、神经网络结构

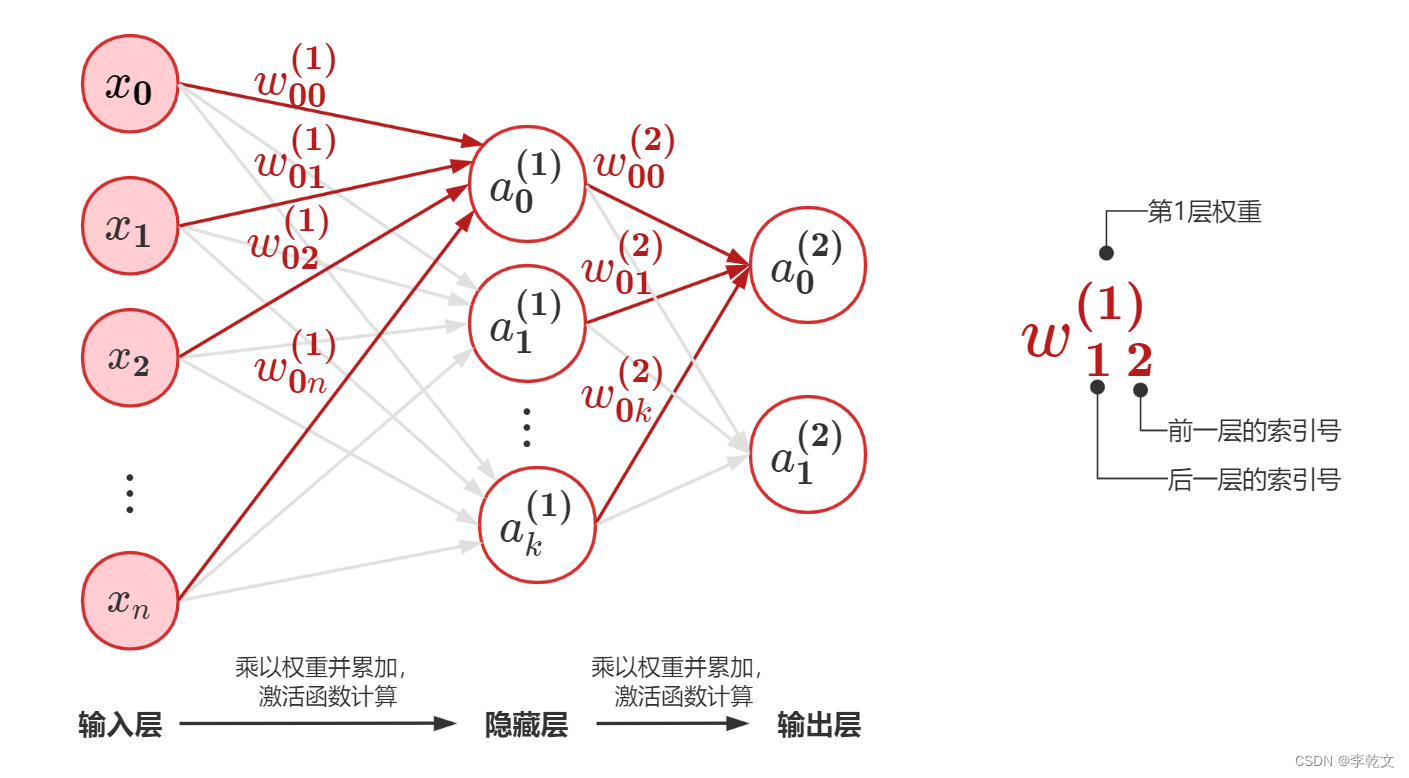
如上图所示（亲绘 ^ _ ^），展示了两层神经网络，有n+1个输入，2个输出，包含1个隐藏层。
其他N层的神经网络以此类推就行。

输入 $x=\left[\begin{array}{c}{x}_0\\ x_1\\ ⋮\\ x_n\end{array}\right]$

第1层权重 $w^{(1)}=\left[\begin{array}{ccccc}{w}_{00}^{(1)}& w_{01}^{(1)}& w_{02}^{(1)}& ...& w_{0n}^{(1)}\\ w_{11}^{(1)}& w_{11}^{(1)}& w_{12}^{(1)}& ...& w_{1n}^{(1)}\\ ...& ...& ...& ...& ...\\ w_{k1}^{(1)}& w_{k1}^{(1)}& w_{k2}^{(1)}& ...& w_{kn}^{(1)}\end{array}\right]$

第1层输出 $a^{(1)}=f_1(w^{(1)}x)=\left[\begin{array}{c}{a}_0^{(1)}\\ a_1^{(1)}\\ ⋮\\ a_k^{(1)}\end{array}\right]$
其中$f_1$是第1层的激活函数。

第2层权重 $w^{(2)}=\left[\begin{array}{ccccc}{w}_{00}^{(2)}& w_{01}^{(2)}& w_{02}^{(2)}& ...& w_{0k}^{(2)}\\ w_{11}^{(2)}& w_{11}^{(2)}& w_{12}^{(2)}& ...& w_{1k}^{(2)}\end{array}\right]$

第2层输出 $a^{(2)}=f_2(w^{(2)}{a}^{(1)})=f_2(w^{(2)}(f_1(w^{(1)}x)))=f_2\left(\left[\begin{array}{ccccc}{w}_{00}^{(2)}& w_{01}^{(2)}& w_{02}^{(2)}& ...& w_{0k}^{(2)}\\ w_{11}^{(2)}& w_{11}^{(2)}& w_{12}^{(2)}& ...& w_{1k}^{(2)}\end{array}\right]\left[\begin{array}{c}{a}_0^{(1)}\\ a_1^{(1)}\\ ⋮\\ a_k^{(1)}\end{array}\right]\right)=\left[\begin{array}{c}{a}_0^{(2)}\\ a_1^{(2)}\end{array}\right]$
其中$f_2$是第2层的激活函数。

三、前向传播

以此类推，那么在第 $l$ 层
$$a^{(l)}=f_l(w^{(l)}{a}^{(l-1)})$$

以$x\underset{f_1}{\overset{w^{(1)}}{\to }}{a}^{(1)}\underset{f_2}{\overset{w^{(2)}}{\to }}\cdots \underset{f_l}{\overset{w^{(l)}}{\to }}{a}^{(l)}$的形式，神经网络通过逐层的信息传递，最终得到网络的输出$a^{(l)}$，这叫前馈神经网络的前向传播。

四、参考资料

神经网络与深度学习-邱锡鹏
《深度学习入门：基于Python的理论与实现》