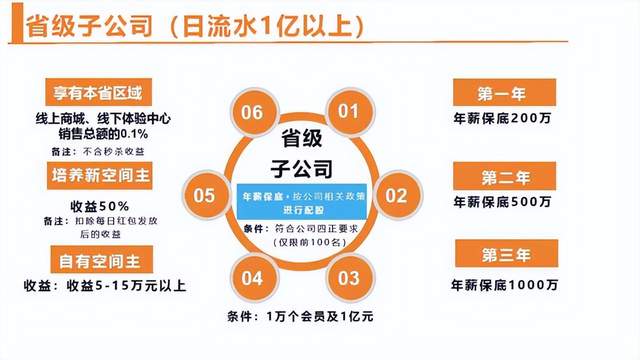
51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例1：

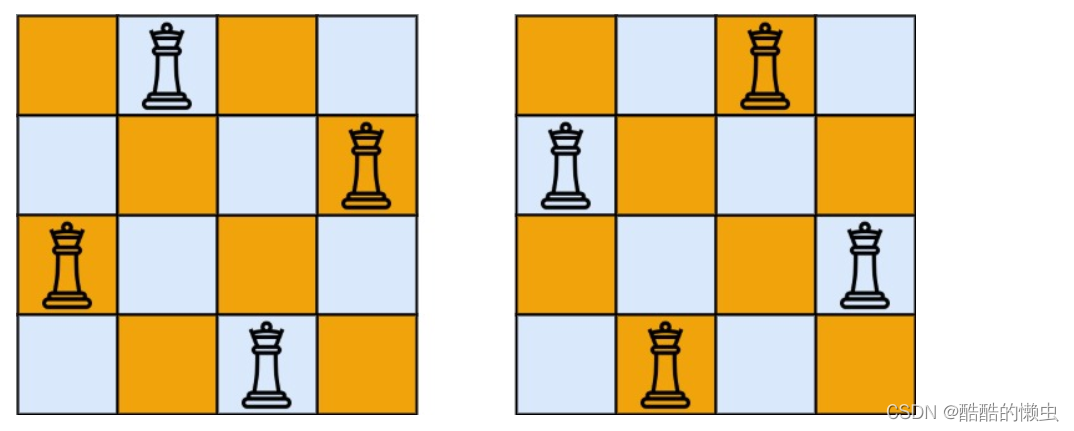
输入：n = 4
输出：[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[[“Q”]]

提示：

• 1 <= n <= 9

思路：(回溯)

在 n*n 的矩阵中摆放 n 个皇后，并且每个皇后不能在同一行，同一列，同一对角线上，求所有的 n 皇后的解。
法一 ：暴力求解；
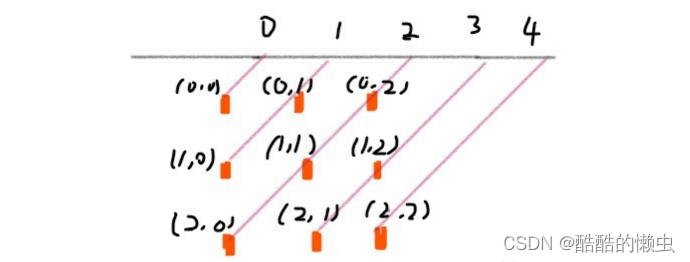
法二 ： 一行一行地摆放，在确定一行中的那个皇后应该摆在哪一列时，需要用三个标记数组来确定某一列是否合法，这三个标记数组分别为：列标记数组、45 度对角线标记数组和 135 度对角线标记数组。

• 45 度对角线标记数组的长度为 2 * n - 1，通过下图可以明确 (r, c) 的位置所在的数组下标为 r + c：
  
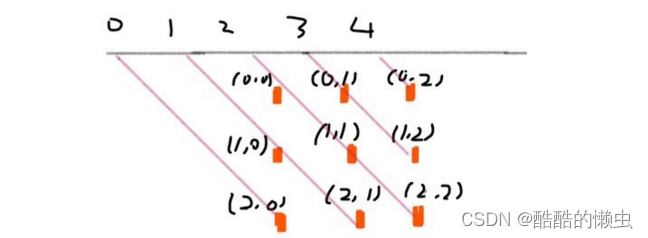
• 135 度对角线标记数组的长度也是 2 * n - 1，(r, c) 的位置所在的数组下标为 n - 1 - (r - c)。
• 

代码：(Java)

法一：

import java.util.ArrayList;
import java.util.List;

public class Nqueen {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int n = 4;
		System.out.println(solveNQueens(n));
	}
	private static int N;
	public static List<List<String>> solveNQueens(int n) {
		List<List<String>> combinations = new ArrayList<>();
		List<String> combination = new ArrayList<>();
		char [][] Q = new char[n][n];
		N = n;
		backtracking(combinations, combination, Q, 0);
		
		return combinations;
	}
	private static void backtracking(List<List<String>> combinations, List<String> combination, char[][] Q, int r) {
		// TODO Auto-generated method stub
		if(r == N) {
			combinations.add(new ArrayList<>(combination));
			return;
		}
		
		for(int i = 0; i < N; i++) {
			if(!tookup(r, i, Q)) {
				continue;
			}
			Q[r][i] = 'Q';
			StringBuffer s = new StringBuffer();
			for(int j = 0; j < N; j++) {
				if(j != i) {
					s.append(".");
				}else {
					s.append("Q");
				}
			}
			combination.add(s.toString());
			backtracking(combinations, combination, Q, r + 1);
			Q[r][i] = ' ';
			combination.remove(combination.size() - 1);
			
		}

	}
	private static boolean tookup(int r, int c, char[][] Q) {
		// TODO Auto-generated method stub
		for(int i = 0; i < N; i++) {
			if(Q[r][i] == 'Q' || Q[i][c] == 'Q') {
				return false;
			}
			if(r-i >= 0 && c-i >= 0 && Q[r-i][c-i] == 'Q')
				return false;
			
			if(r+i < N && c+i < N && Q[r+i][c+i] == 'Q')
				return false;
			
			if(r+i < N && c-i >= 0 && Q[r+i][c-i] == 'Q')
				return false;
			
			if(r-i >= 0 && c+i < N && Q[r-i][c+i] == 'Q')
				return false;
		}
		return true;
	}
}

法二：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Nqueen {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int n = 4;
		System.out.println(solveNQueens(n));
	}
	
	private static List<List<String>> solutions;
	private static char[][] nQueens;
	private static boolean[] colUsed;
	private static boolean[] diagonals45Used;
	private static boolean[] diagonals135Used;
	private static int N;

	public static List<List<String>> solveNQueens(int n) {
	    solutions = new ArrayList<>();
	    nQueens = new char[n][n];
	    for (int i = 0; i < n; i++) {
	        Arrays.fill(nQueens[i], '.');
	    }
	    colUsed = new boolean[n];
	    diagonals45Used = new boolean[2 * n - 1];
	    diagonals135Used = new boolean[2 * n - 1];
	    N = n;
	    backtracking(0);
	    return solutions;
	}

	private static void backtracking(int row) {
	    if (row == N) {
	        List<String> list = new ArrayList<>();
	        for (char[] chars : nQueens) {
	            list.add(new String(chars));
	        }
	        solutions.add(list);
	        return;
	    }

	    for (int col = 0; col < N; col++) {
	        int diagonals45Idx = row + col;
	        int diagonals135Idx = N - 1 - (row - col);
	        if (colUsed[col] || diagonals45Used[diagonals45Idx] || diagonals135Used[diagonals135Idx]) {
	            continue;
	        }
	        nQueens[row][col] = 'Q';
	        colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = true;
	        backtracking(row + 1);
	        colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = false;
	        nQueens[row][col] = '.';
	    }
	}
}

运行结果：

注：仅供学习参考！

题目来源：力扣.