1. 旋转数组中的最小数字

原题链接：

剑指 Offer 11. 旋转数组的最小数字 - 力扣（LeetCode）https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/

1.1 题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

1.2 思路一

从头到尾遍历数组，找出最小的元素即可。这种思路的时间复杂度是O(N)，这种思路并没有利用旋转数组的特性，显然不是最优的解法。

int minArray(int* numbers, int numbersSize)
{
    int min = numbers[0];
    for(int i = 0; i < numbersSize; i++)
    {
        if(numbers[i]<min)
        {
            min = numbers[i];
        }
    }
    return min;
}

1.3 思路二

如果在做题的过程中要求在排序的数组（或者部分排序的数组中）中查找一个数字或者统计某个数字出现的次数，那么我们都可以尝试使用二分查找算法。

我们发现旋转数组可以划分成两个排序的子数组，而且前面子数组的元素都大于或者等于后面子数组的元素（数组元素可以重复嘛）。并且最小的元素恰好是这两个子数组的分界线，根据题意我们可以利用二分查找算法实现O(logN)的查找。下面的折线图能帮助大家理解：

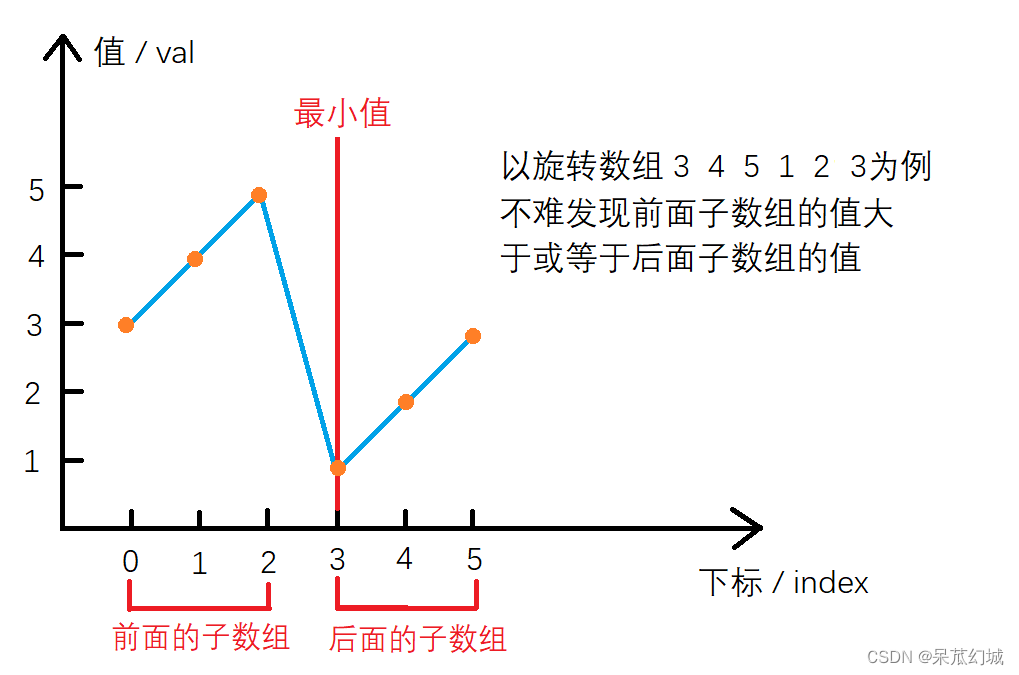
基于二分查找的基本思路，我们维护三个指针，begin，end，mid。一开始让他们分别指向数组的首元素，末尾的元素，和中间的元素，然后比较mid指向的元素与end指向的元素的大小关系：

情况一：mid指向的元素大于end指向的元素，根据上面发现的规律：前面的子数组大于等于后面的子数组。说明此时mid指向的元素在前面的子数组中，我们让begin = mid + 1 从而缩小查找的范围。

情况二：mid指向的元素小于end指向的元素，因为两个子数组都是升序序列（说非降序序列似乎更严谨），而end是指向待查找数组的末尾元素，所以mid必然是指向后面的子数组中的元素，此时我们令end = mid，缩小查找范围。为啥上面是begin = mid + 1，而下面是end = mid ，不是

end = mid - 1嘞，我们通过下面的例子来分析：

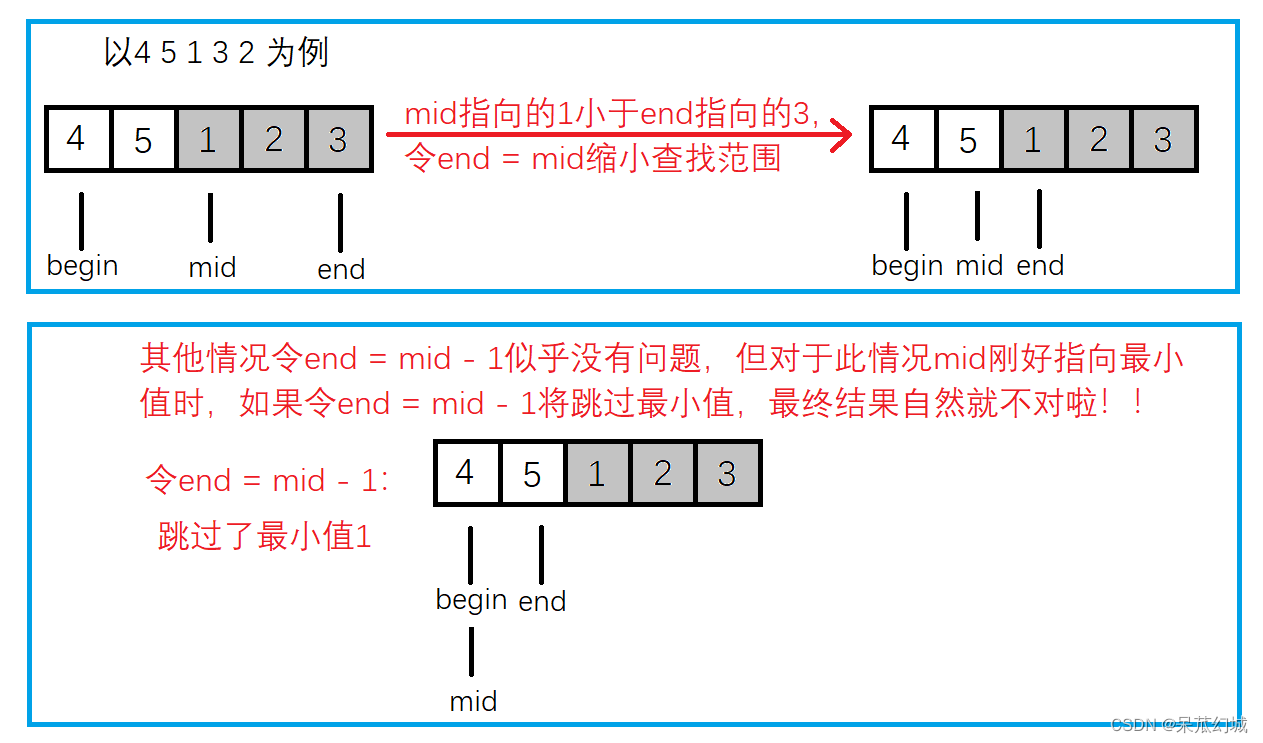
因为当mid恰好指向最小的元素时是属于情况二的，不存在令begin = mid + 1跳过最小值的情况。

情况三：当mid指向的值等与end指向的值：此时我们是没有办法判定最小值位于哪一边的。

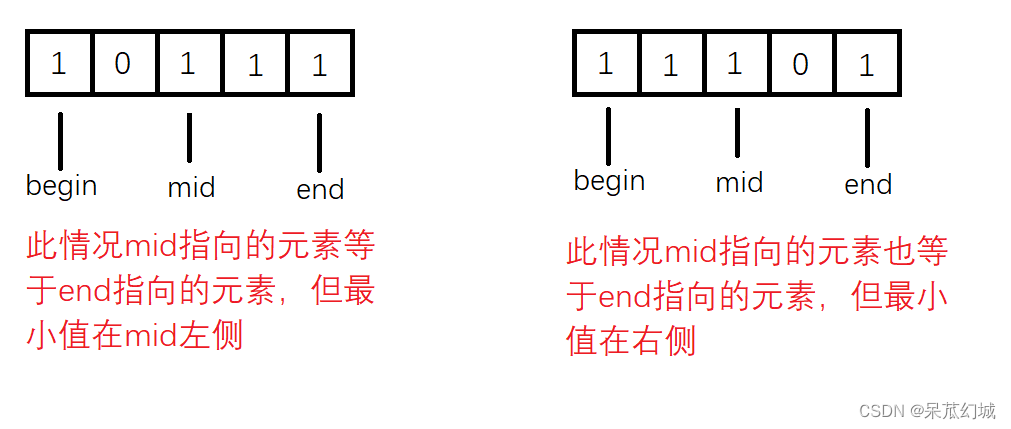
此时我们令end - 1以这种方式更新mid的位置，虽然令end - 1丢失了一个数据，但是因为mid指向的元素与end指向的元素是相等的，无论丢失的数据是否是最小值，都无关紧要。切记不可以令begin++，因为我们比较的是mid与end之间的关系，end--不会丢失数据，但begin++会丢失数据，影响最终的结果。

关于返回值：因为循环结束时begin，end是相等的，所以我们返回begin指向的元素，或者end指向的元素都可以，注意：mid可不一定等于begin 或者 end，不可返回mid指向的元素。

还有一种情况就是当数组为非降序序列时，这个代码也能解决哦！但是做题一定要想到这种特殊的情况奥！

例如：1 2 3 4 5


int minArray(int* numbers, int numbersSize){
    int begin = 0;
    int end = numbersSize - 1;
    int mid;
    while(begin < end)
    {
        mid = begin + ((end - begin)>>1);
        if(numbers[mid] > numbers[end])
            begin = mid + 1;
        else if(numbers[mid] < numbers[end])
            end = mid;
        else
            end--;
    }
    return numbers[begin];
}

1.4 小试牛刀

链接：

33. 搜索旋转排序数组 - 力扣（LeetCode）https://leetcode.cn/problems/search-in-rotated-sorted-array/

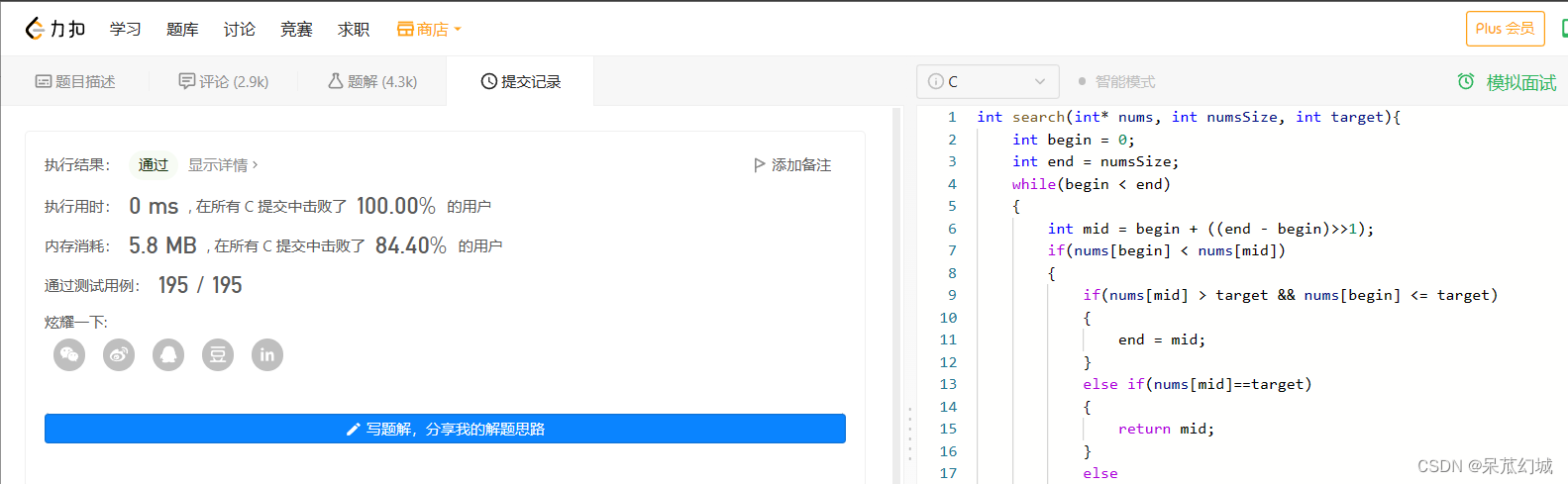
这道题的关键就是确定target的位置，我觉得是这样哈！

int search(int* nums, int numsSize, int target){
    int begin = 0;
    int end = numsSize;
    while(begin < end)
    {
        int mid = begin + ((end - begin)>>1);
        if(nums[begin] < nums[mid])
        {
            if(nums[mid] > target && nums[begin] <= target)
            {
                end = mid;
            }
            else if(nums[mid]==target)
            {
                return mid;
            }
            else
            {
                begin = mid + 1;
            }
        }
        else
        {
            if(nums[mid] < target && nums[end-1]>=target)
            {
                begin = mid + 1;
            }
            else if(nums[mid]==target)
            {
                return mid;
            }
            else
            {
                end = mid;
            }
        }

    }
    return -1;
}