前言

接上篇说到，小A匆匆忙忙的赶回宿舍，因为晚上他要给女神整理讲解MySQL中索引数据结构资料。一边整理一边忍住不笑了起来，等小美看到这篇文章不得爱上自己。当上小美男朋友，从此踏上人生巅峰不是梦（该考虑一下孩子叫啥了）。

擦擦口水，抓紧整理一下资料，小美还在等着我呢！

正文

在讲解B+树之前先了解一下树的整体结构，无非就是二叉树、二叉搜索树、平衡二叉树，更高级一点的有红黑树、B树、B+树等等。而树的查找性能取决于树的高度，让树尽可能平衡是为了降低树的高度。

首先需要了解下为啥MySQL会选用B+树的结构，我们来看看其他的树形结构是咋样的。

二叉树

二叉树的每一个节点都只有两个子节点，当需要向其插入更多的数据的时候，就必须要增加树的高度，而增加树的高度会导致IO的次数变多，对于二叉树而言，它的查找操作的时间复杂度就是树的高度，树的高度越高查询性能会随着数据的增多越来越低。

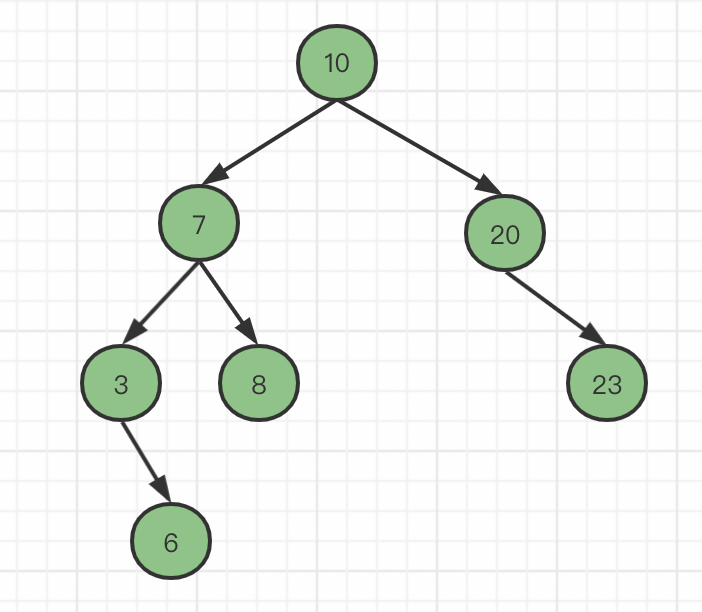
二叉树节点中，还存在非正常的倾斜（比如ID自增的情况）的二叉树，查询一次数据就相当于与全表搜索。

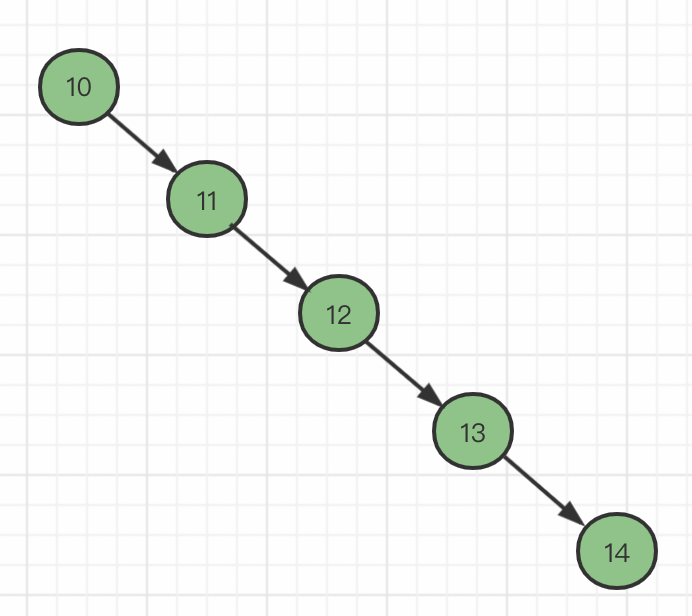
很明显二叉树的查询性能特别差！

红黑树

红黑树一种平衡二叉树，它复杂的定义和规则都是为了保证树的平衡性。

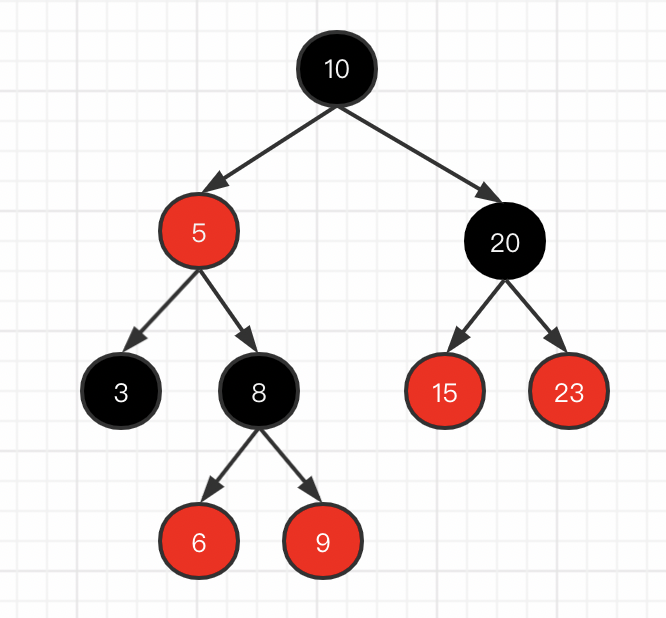
红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡。但是树的高度不可控，导致红黑树由于树的高度太高需要进行多次磁盘IO，在数据量较大的情况下不可取（磁盘IO的次数和树的高度强有关）。而且红黑树也需要不断的调整平衡性，也需要消耗性能。

B树

B树是一种多路搜索树，它的每个节点都可以拥有多于两个孩子节点。M路的B树最多拥有M个孩子节点，设计成多路是为了降低树的高度。

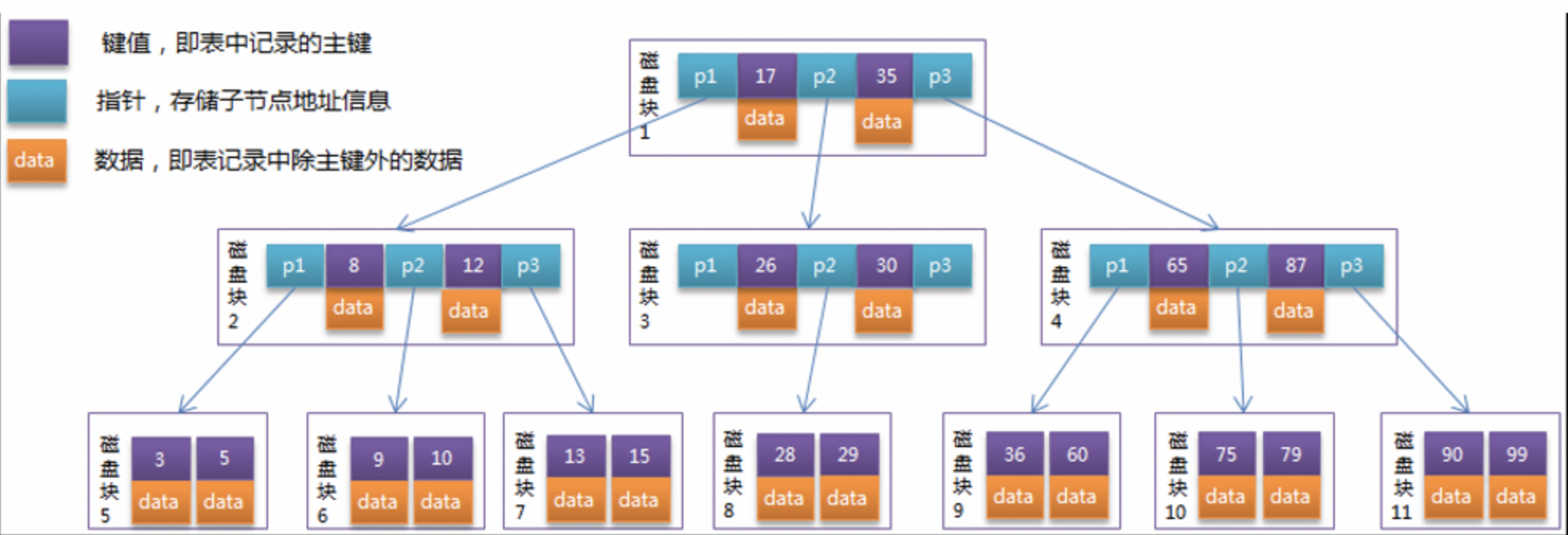
由于B树的索引节点既要存索引信息，又要存其对应的数据信息，每个节点一次I/O操作就可以完全载入索引及对应数据。

操作系统从磁盘的索引文件中，一次读取一个节点大小到内存中构建B树，然后在节点中二分搜索元素，如果发现值大于根节点的所有数据值，那么就继续从磁盘的索引文件中把该节点的右孩子节点加载到内存上，然后进行二分搜索查找，以此类推下去。但是由于每一个节点的存储空间是有限的，数据空间占用较大时，就会导致每个节点存储的索引信息就会减少（即树的分支变少），同样会导致B树的高度较高，磁盘IO次数花费增大，效率变低。

B+树

B+树是在B树基础上的一种优化，使其更适合外存储索引结构，MySQL底层使用的就是B+数结构。

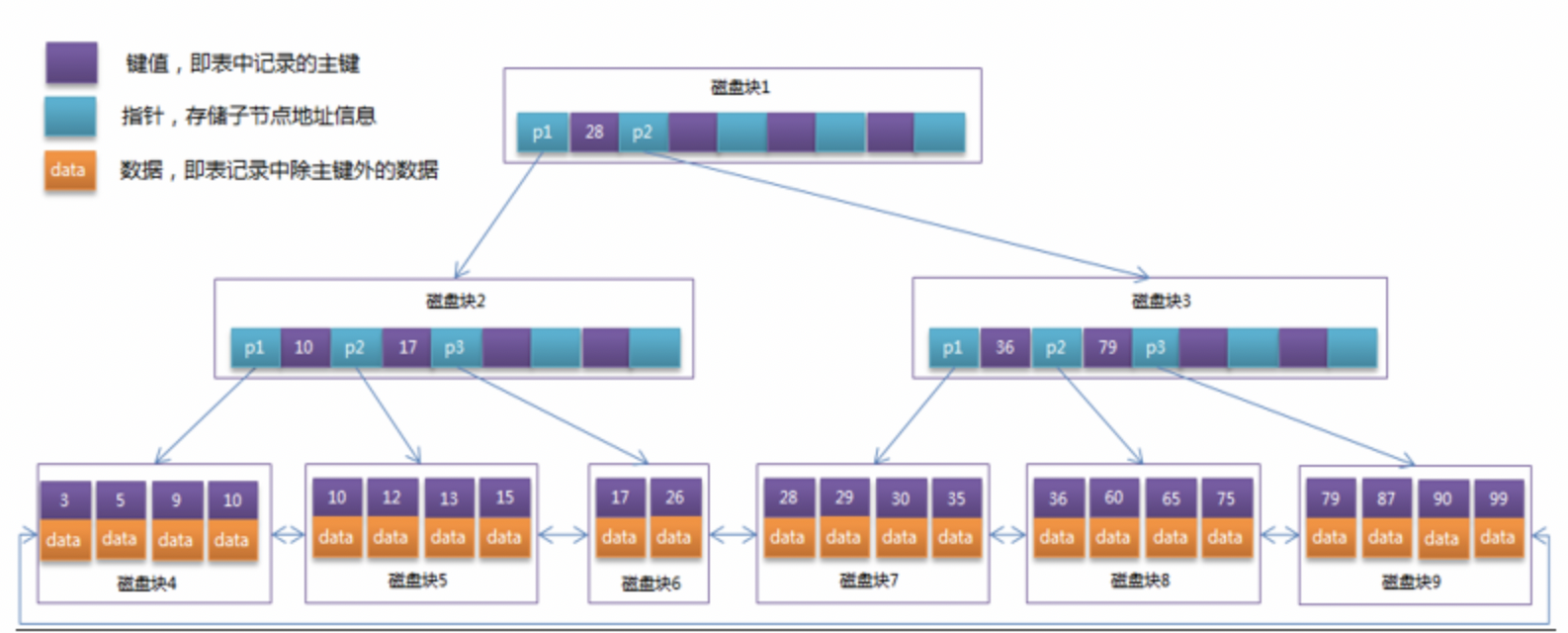
可以看到B+树有以下几个特点：

非叶子节点相当于是叶子节点的索引，不存储数据，叶子节点用于存储关键字以及数据。即每个B+树非叶子节点相对于B树的叶子节点能存储更多的key，这样树的高度就更低，花费的磁盘I/O就更少，查找更快。
由于数据全部存在于叶子节点，所以无论查找哪个数据，花费的磁盘I/O次数都是一样的，查找数据耗费的时间比较稳定
叶子节点被串在链表中，形成了一个有序链表。做范围搜索和整表遍历的时候直接遍历这个有序链表即可，不用遍历平衡树。

为什么选用B+树结构？

相信通过以上的了解后，大家对如何回答这道面试题也有基本思路，我们来总结回答一下。

DML语句执行时如果命中索引，数据库引擎会向内核申请从磁盘读取索引文件到内存中，每次通过IO读取一个节点的数据并在内存中构建成B+树结构。之所以选用B+树结构的主要原因是因为B+树每层可以有M个节点从而降低树的高度，且非叶子结点只存储索引Key，由叶子结点来存储数据，可以保证每个非叶子结点可以存储更多的索引Key，进一步降低树的高度，从而减少IO次数提升执行性能。最后叶子结点是用双写链表连接起来，可以支持范围查询或整表遍历，B+树的整体特点使DML语句执行性能有极大的提升。