目录
哈希
常见哈希函数
除留余数法
哈希冲突
哈希冲突解决
闭散列
a、线性探测
插入
查找
删除
线性探测的实现代码
b、二次探测
二次探测的实现
开散列
开散列实现
插入
查找
删除
析构函数
代码汇总
哈希
常见哈希函数
-
直接定址法 -- (常用) -- 不存在哈希冲突
取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B
优点：简单、均匀
缺点：需要事先知道关键字的分布情况
使用场景：适合查找比较小且连续的情况（常见：计数排序）
- 除留余数法 -- (常用) -- 存在哈希冲突，重点解决哈希冲突
设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址
（本文重点）
- 平方取中法 -- (了解) -- 存在哈希冲突，只能适用于整数
假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址；
再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址
平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况
- 折叠法 -- (了解) -- 不存在哈希冲突，只能适用于整数
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些)，然后将这 几部分叠加求和，并按散列表表长，取后几位作为散列地址。
折叠法适合事先不需要知道关键字的分布，适合关键字位数比较多的情况。
- 随机数法 -- (了解)
选择一个随机函数，取关键字的随机函数值为它的哈希地址，即H(key) = random(key),其中 random为随机数函数。
随机数法通常应用于关键字长度不等时。
-
数学分析法 -- (了解)
设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各位上出现的频率不一定相同，可能在某些位上分布比较均匀，每种符号出现的机会均等，在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小，选择其中各种符号分布均匀的若干位作为散列地址。例如：
假设要存储某家公司员工登记表，如果用手机号作为关键字，那么极有可能前7位都是相同的，那么我们可以选择后面的四位作为散列地址，如果这样的抽取工作还容易出现 冲突，还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法。
数字分析法通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的
若干位分布较均匀的情况。
除留余数法
哈希基于映射，值跟存储位置建立关联映射关系。以我们就学过计数排序，实现的原理是：
利用映射，取最大值到最小值的大小建立数组通过唯一的对应关系，利用映射关系计数排序，正是因为此计数排序也有巨大的缺陷，由于数组大小取决最大值与最小值，如果遇见：3 7 19 300 70000，仅仅5个数据就要创建70000个空间，而哈希利用除留余数法建立关联映射关系：
设散列表中允许的地址数为m，取一个不大于m，但最接近或者等于m的质数p作为除数，
按照哈希函数：Hash(key) = key% p(p<=m),将关键码转换成哈希地址。
以p == 10为例：
哈希冲突
不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。 把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。
哈希冲突解决
解决哈希冲突两种常见的方法是：闭散列和开散列
- 闭散列 -- 开放定址法
- a、线性探测
- b、二次探测
- 开散列 -- 拉链法/哈希桶（此方法更好，也是库中所用的）
闭散列
a、线性探测
如，下列场景，现在需要插入元素44，先通过哈希函数计算哈希地址，为4（44%10 = 4），因此44理论上应该插在该位置，但是该位置已经放了值为4的元素，即发生哈希冲突：
线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。
插入
- 通过哈希函数获取待插入元素在哈希表中的位置。
-
如果该位置中没有元素则直接插入新元素，如果该位置中有元素发生哈希冲突， 使用线性探测找到下一个空位置，插入新元素。
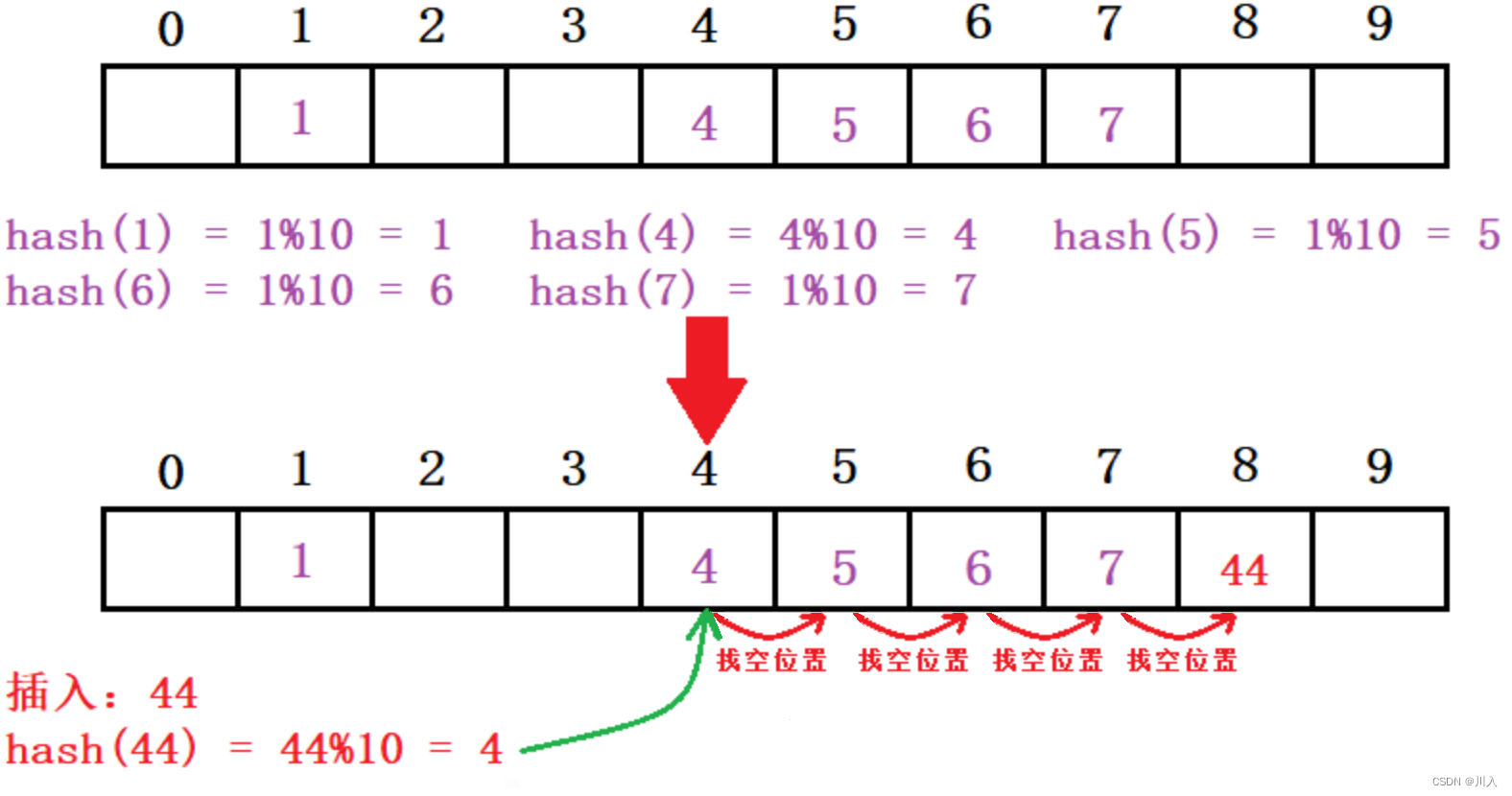
从此可以看出闭散列的线性探测是不好的，容易数据之间过于的占用位置，造成互相影响，但是其也是有效的方式。（冲突越多效率越低）
查找
- 根据插入的规则，如果数据存在。即，数据一定在：该哈希地址位置，或者在地址位置后连续不为空的序列里，否则无该值。
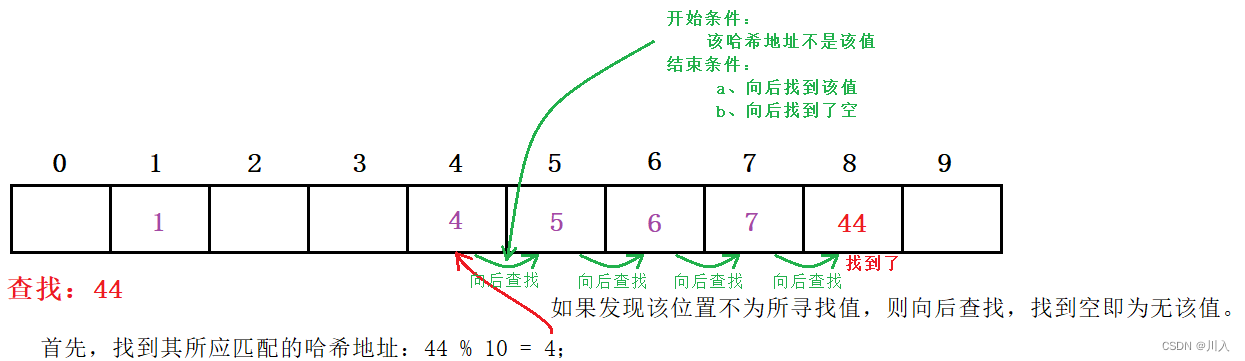
删除
- 采用闭散列处理哈希冲突时，不能随便物理删除哈希表中已有的元素，若直接删除元素会影响其他元素的搜索。
- 线性探测采用标记的伪删除法来删除一个元素。
为什么以伪删除法来删除一个元素？
如果我们不用伪删除法来删除一个元素：
伪删除法：加一个状态标志位
// 哈希表每个空间给个标记
// EMPTY此位置空， EXIST 此位置已经有元素， DELETE 元素已经删除enum State { EMPTY , EXIST , DELETE };
即：删除的时候并不是标为空，而是标为删除。这样查找的时候看EMPTY，EMPTY是无该数据。插入的是时候看是DELETE还是EMPTY，是DELETE更改数据，是EMPTY填补数据。
线性探测的实现代码
由于key值需要进行%数求哈希地址为，遇见能强转为size_t的还好，但是如果遇见的是string之类不能强转的就会出现问题，所以我们需要利用仿函数来解决此类问题，对于能强转的我们提供成默认的仿函数，并利用特化提供string类型的，其余不能强转的同理。
字符串哈希算法
#include<vector>
#include<utility>
#include<iostream>
#include<string>
using namespace std;
enum State
{
EMPTY, //没有元素
EXIST, //存在元素
DELETE //该元素已被删除
};
// 单位数据
template<class K, class V>
struct HashData
{
pair<K, V> _kv;
State _state = EMPTY;
};
// 仿函数为了防止出现Key是string的存在，因为string不能直接%，其余不能直接%同理
//能强转的
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return size_t(key);
}
};
//由于string不能强转为size_t，需要显示写仿函数，特化
template<>
struct HashFunc<string>
{
// BKDR
size_t operator()(const string& key)
{
size_t val = 0;
for (auto ch : key)
{
val *= 131;
val += ch;
}
return val;
}
};
template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
Hash hash;
//插入
bool Insert(const pair<K, V>& kv)
{
// 防止已有该值
if (Find(kv.first))
return false;
//哈希表的扩容
if (_tables.size() == 0 || 10 * _size / _tables.size() >= 7) // 散列表的载荷因子：a = 填入表中的元素个数 / 散列表的长度。(此处7为规定的载荷因子)
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
// size变大，即%数变大，哈希地址改变，需要重新insert。
HashTable<K, V> newHT;
newHT._tables.resize(newSize);
for (auto e : _tables)
{
if (e._state == EXIST)
newHT.Insert(e._kv);
}
_tables.swap(newHT._tables);
}
size_t hashi = hash(kv.first) % _tables.size(); //此处%的是size是因为底层为vector实现，而其opertor[]的范围规定为size
// 哈希表是通过：size大小的列表的如同头与尾相接，以循环寻找插入位置。
// （由于引入了载荷因子，列表不可能满）
while (_tables[hashi]._state != EMPTY)
{
hashi++;
hashi %= _tables.size();
}
// 插入数据
_tables[hashi]._kv = kv;
_tables[hashi]._state = EXIST;
_size++;
return true;
}
//查找
HashData<K, V>* Find(const K& key)
{
if (_tables.size() == 0)
{
return nullptr;
}
size_t state = hash(key) % _tables.size();
size_t hashi = state;
while (_tables[hashi]._state != EMPTY)
{
if (_tables[hashi]._state != DELETE && _tables[hashi]._kv.first == key)
return &_tables[hashi];
hashi++;
hashi %= _tables.size();
if (hashi == state) // 防止出现边删除边插入而导致的，不超过载荷因子下而存满（概率极低）
break;
}
return nullptr;
}
//删除
bool Erase(const K& key)
{
HashData<K, V>* ret = Find(key);
if (ret)
{
ret->_state = DELETE;
--_size;
return true;
}
else
return false;
}
//打印存在的数据
void Print()
{
for (size_t i = 0; i < _tables.size(); ++i)
{
if (_tables[i]._state == EXIST)
cout << "[" << i << "]:" << _tables[i]._kv.first << " ";
}
}
private:
vector<HashData<K, V>> _tables;
size_t _size = 0; //存储多少个有效数据
};
void TestHash()
{
HashTable<int, int> h;
int array[] = { 1, 5, 8, 33, 77, 36, 86, 1, 8, 5, 8, 2, 5 };
for (auto e : array)
{
h.Insert(make_pair(e, e));
}
h.Erase(1);
h.Erase(6);
cout << h.Find(1) << endl;
cout << h.Find(8) << endl;
h.Print();
}
void TestHashString()
{
HashTable<string, int> h;
string array[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
for (auto ch : array)
h.Insert(make_pair(ch, 1));
h.Print();
}
int main()
{
TestHash();
TestHashString();
return 0;
}
哈希表线性探测进行扩容方式
如 a = 0.7即：填入表中的元素个数只能是散列表长度的70%。当大于就扩容。
- 线性探测优点：实现非常简单。
- 线性探测缺点：一旦发生哈希冲突，所有的冲突连在一起，容易产生数据“堆积”，即：不同 关键码占据了可利用的空位置，使得寻找某关键码的位置需要许多次比较，导致搜索效率降低。
b、二次探测
二次探测的实现
二次探测的实现与线性探测的实现的核心是极为相似的，也就是对于哈希地址取值方式的改变。
#include<string>
#include<vector>
#include<iostream>
using namespace std;
enum State
{
EMPTY,
EXIST,
DELETE
};
template<class K, class V>
struct HashData
{
pair<K, V> _kv;
State _state = EMPTY;
};
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
// 特化
template<>
struct HashFunc<string>
{
// BKDR
size_t operator()(const string& key)
{
size_t val = 0;
for (auto ch : key)
{
val *= 131;
val += ch;
}
return val;
}
};
template<class K, class V, class Hash = HashFunc<K>>
class HashTable
{
public:
bool Insert(const pair<K, V>& kv)
{
if (Find(kv.first))
return false;
// 负载因子到了就扩容
if (_tables.size() == 0 || 10 * _size / _tables.size() >= 7) // 扩容
{
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
HashTable<K, V, Hash> newHT;
newHT._tables.resize(newSize);
// 旧表的数据映射到新表
for (auto e : _tables)
{
if (e._state == EXIST)
newHT.Insert(e._kv);
}
_tables.swap(newHT._tables);
}
Hash hash;
size_t start = hash(kv.first) % _tables.size();
size_t i = 0;
size_t hashi = start;
// 二次探测
while (_tables[hashi]._state == EXIST)
{
++i;
hashi = start + i * i;
hashi %= _tables.size();
}
_tables[hashi]._kv = kv;
_tables[hashi]._state = EXIST;
++_size;
return true;
}
HashData<K, V>* Find(const K& key)
{
if (_tables.size() == 0)
return nullptr;
Hash hash;
size_t start = hash(key) % _tables.size();
size_t hashi = start;
int i = 0;
while (_tables[hashi]._state != EMPTY)
{
if (_tables[hashi]._state != DELETE && _tables[hashi]._kv.first == key)
return &_tables[hashi];
i++;
hashi = start + i * i;
hashi %= _tables.size();
if (hashi == start)
break;
}
return nullptr;
}
bool Erase(const K& key)
{
HashData<K, V>* ret = Find(key);
if (ret)
{
ret->_state = DELETE;
--_size;
return true;
}
return false;
}
void Print()
{
for (size_t i = 0; i < _tables.size(); ++i)
{
cout << "[" << i << "]:" << _tables[i]._kv.first << " ";
}
cout << endl;
}
private:
vector<HashData<K, V>> _tables;
size_t _size = 0; //存储的数据个数
};
void TestTable()
{
HashTable<int, int> h;
int array[] = { 1,6,545,876,235,8765,41 };
for (auto e : array)
{
h.Insert(make_pair(e, e));
}
cout << h.Find(545) << endl;
h.Erase(545);
cout << h.Find(545) << endl;
h.Print();
}
int main()
{
TestTable();
return 0;
}总的来说闭散列是不好的，可以说是被淘汰的，但是意识一种值得学习的是思维。其作为哈希实现的一种思维结构，闭散列以这种开放定址法，总是会由于冲突而去占用别的位置。于是便有为解决冲突的开散列的桶式结构 —— 拉链法/哈希桶。
开散列
开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地
址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链
接起来，各链表的头结点存储在哈希表中。
从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。（1、11、21冲突。2、12冲突），
每一个单链表各自称为一个桶
。
开散列实现
对于增删查，皆与单链表的实现相识。本质上就是多个单链表放入数组中。
由于存储的数据可能是string之类，无法直接强转为size_t的类型，所以我们需要使用仿函数实现：
namespace cr
{
// 哈希桶中的单链表的节点
template<class K, class V>
struct HashNode
{
pair<K, V> _data;
HashNode<K , V>* _next;
HashNode(const pair<K, V>& data)
:_data(data)
, _next(nullptr)
{}
};
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
// 特化
template<>
struct HashFunc<string>
{
size_t operator()(const string& key)
{
size_t count = 0;
for (auto ch : key)
{
count *= 131;
count += ch;
}
return count;
}
};
// 哈希桶的封装实现
template<class K, class V, class Hash = HashFunc<K>>
class HashBucket
{
private:
typedef HashNode<K, V> Node;
public:
//……
private:
vector<Node*> _tables; // 哈希表
size_t _size = 0; // 有效数据个数
};
}插入
由于是单链表，并且哈希桶并未要求对数据进行排序，所以表中的每一个单链表，进行尾插还是头插都是可以的，此处选择头插。
对于空间的扩容，根据相关实验素数的效率更高，于是哈希桶的空间开辟是根据素数数组开辟的：
// 提取空间开辟的大小（素数）
inline size_t __stl_next_prime(size_t n)
{
static const size_t __stl_num_primes = 28;
static const size_t __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
//4294967291个int类型已经是16G，大小已经足够。
for (size_t i = 0; i < __stl_num_primes; ++i)
{
if (__stl_prime_list[i] > n)
return __stl_prime_list[i];
}
return -1;
}// 插入
bool Insert(const pair<K, V>& key)
{
//查重
if (Find(key.first))
return false;
Hash hash;
// 扩容
if (_size == _tables.size())
{
vector<Node*> newTables;
newTables.resize(__stl_next_prime(_size), nullptr);
// 将旧表数据移动到新表
for (size_t i = 0; i < _tables.size(); ++i)
{
// 将旧表的每个哈希桶的单链表节点移动到新表上
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hash(key.first) % newTables.size(); // 在新表上的哈希地址
// 在新表的哈希地址上头插
cur->_next = newTables[hashi];
newTables[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
// 找到哈希地址并进行头插
size_t hashi = hash(key.first) % _tables.size();
Node* cur = new Node(key);
cur->_next = _tables[hashi];
_tables[hashi] = cur;
++_size;
return true;
}查找
算哈希地址后根据哈希地址遍历该地址的桶查找。
// 查找
Node* Find(const K& key)
{
if (_tables.size() == 0) // 未存入数据
return nullptr;
Hash hash;
size_t hashi = hash(key) % _tables.size();
Node* cur = _tables[hashi];
while (cur)
{
if (cur->_data.first == key)
return cur;
cur = cur->_next;
}
return nullptr;
}
删除
根据哈希地址寻找后，直接按照单链表的删除方式即可。
// 删除
bool Erase(const K& key)
{
if (_tables.size() == 0) // 未存入数据
return false;
Hash hash;
size_t hashi = hash(key) % _tables.size();
Node* cur = _tables[hashi];
Node* prev = nullptr;
while (cur)
{
if (cur->_data.first == key) // 找到需删除的数据
{
if (prev == nullptr) // 删除的是桶的第一个数据
_tables[hashi] = cur->_next;
else
prev->_next = cur->_next;
delete cur;
--_size;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}析构函数
由于是单链表，是new的空间，所以需要写析构函数，对一个一个节点释放。
~HashBucket()
{
for (size_t i = 0; i < _tables.size(); ++i)
{
// 一个节点一个节点的释放
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}代码汇总
#include<iostream>
#include<utility>
#include<vector>
#include<time.h>
using namespace std;
namespace cr
{
// 哈希桶中的单链表的节点
template<class K, class V>
struct HashNode
{
pair<K, V> _data;
HashNode<K , V>* _next;
HashNode(const pair<K, V>& data)
:_data(data)
, _next(nullptr)
{}
};
template<class K>
struct HashFunc
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
// 特化
template<>
struct HashFunc<string>
{
size_t operator()(const string& key)
{
size_t count = 0;
for (auto ch : key)
{
count *= 131;
count += ch;
}
return count;
}
};
// 哈希桶的封装实现
template<class K, class V, class Hash = HashFunc<K>>
class HashBucket
{
private:
typedef HashNode<K, V> Node;
public:
~HashBucket()
{
for (size_t i = 0; i < _tables.size(); ++i)
{
// 一个节点一个节点的释放
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
delete cur;
cur = next;
}
_tables[i] = nullptr;
}
}
// 提取空间开辟的大小（素数）
inline size_t __stl_next_prime(size_t n)
{
static const size_t __stl_num_primes = 28;
static const size_t __stl_prime_list[__stl_num_primes] =
{
53, 97, 193, 389, 769,
1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433,
1572869, 3145739, 6291469, 12582917, 25165843,
50331653, 100663319, 201326611, 402653189, 805306457,
1610612741, 3221225473, 4294967291
};
//4294967291个int类型已经是16G，大小已经足够。
for (size_t i = 0; i < __stl_num_primes; ++i)
{
if (__stl_prime_list[i] > n)
return __stl_prime_list[i];
}
return -1;
}
// 插入
bool Insert(const pair<K, V>& key)
{
//查重
if (Find(key.first))
{
return false;
}
Hash hash;
// 扩容
if (_size == _tables.size())
{
vector<Node*> newTables;
newTables.resize(__stl_next_prime(_size), nullptr);
// 将旧表数据移动到新表
for (size_t i = 0; i < _tables.size(); ++i)
{
// 将旧表的每个哈希桶的单链表节点移动到新表上
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hash(key.first) % newTables.size(); // 在新表上的哈希地址
// 在新表的哈希地址上头插
cur->_next = newTables[hashi];
newTables[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newTables);
}
// 找到哈希地址并进行头插
size_t hashi = hash(key.first) % _tables.size();
Node* cur = new Node(key);
cur->_next = _tables[hashi];
_tables[hashi] = cur;
++_size;
return true;
}
// 查找
Node* Find(const K& key)
{
if (_tables.size() == 0) // 未存入数据
return nullptr;
Hash hash;
size_t hashi = hash(key) % _tables.size();
Node* cur = _tables[hashi];
while (cur)
{
if (cur->_data.first == key)
return cur;
cur = cur->_next;
}
return nullptr;
}
// 删除
bool Erase(const K& key)
{
if (_tables.size() == 0) // 未存入数据
return false;
Hash hash;
size_t hashi = hash(key) % _tables.size();
Node* cur = _tables[hashi];
Node* prev = nullptr;
while (cur)
{
if (cur->_data.first == key) // 找到需删除的数据
{
if (prev == nullptr) // 删除的是桶的第一个数据
_tables[hashi] = cur->_next;
else
prev->_next = cur->_next;
delete cur;
--_size;
return true;
}
prev = cur;
cur = cur->_next;
}
return false;
}
// 有效数据个数
size_t Size()
{
return _size;
}
// 表的长度
size_t TablesSize()
{
return _tables.size();
}
// 桶的个数
size_t BucketNum()
{
size_t num = 0;
for (size_t i = 0; i < _tables.size(); ++i)
{
if (_tables[i])
++num;
}
return num;
}
// 桶的最长长度
size_t MaxBucketLenth()
{
size_t maxLen = 0;
for (size_t i = 0; i < _tables.size(); ++i)
{
size_t len = 0;
Node* cur = _tables[i];
while (cur)
{
++len;
cur = cur->_next;
}
if (len > maxLen)
maxLen = len;
}
return maxLen;
}
private:
vector<Node*> _tables; // 哈希表
size_t _size = 0; // 有效数据个数
};
void TestHT()
{
int n = 19000000;
vector<int> v;
v.reserve(n);
srand(time(0));
//rand()所提供的数最多位3万多，所以在远大于3万会大量数重复
for (int i = 0; i < n; ++i)
{
//v.push_back(i);
v.push_back(rand() + i); // 重复少
//v.push_back(rand()); // 重复多
}
size_t begin1 = clock();
HashBucket<int, int> hb;
for (auto e : v)
{
hb.Insert(make_pair(e, e));
}
size_t end1 = clock();
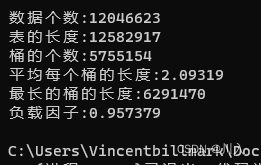
cout << "数据个数:" << hb.Size() << endl;
cout << "表的长度:" << hb.TablesSize() << endl;
cout << "桶的个数:" << hb.BucketNum() << endl;
cout << "平均每个桶的长度:" << (double)hb.Size() / (double)hb.BucketNum() << endl;
cout << "最长的桶的长度:" << hb.MaxBucketLenth() << endl;
cout << "负载因子:" << (double)hb.Size() / (double)hb.TablesSize() << endl;
}
}
int main()
{
cr::TestHT();
return 0;
}
