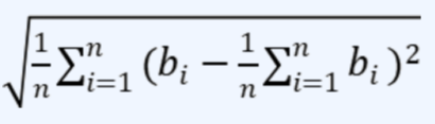目录
一、前言
二、例题1——修剪灌木
三、例题2—— 付账问题
四、例题3——最少砝码
五、例题四——矩形拼接
六、例题五——蜂巢
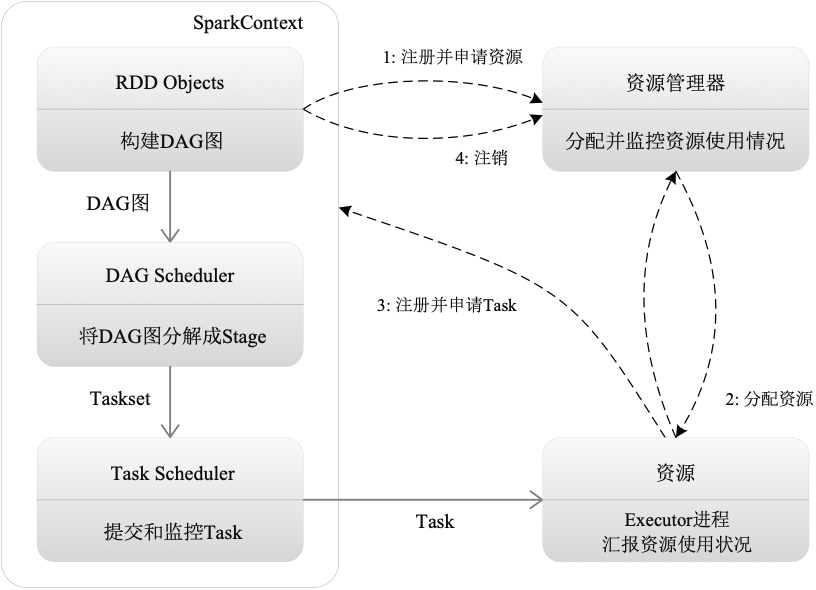
一、前言
竞赛题有很多不需要什么算法的题目,只要学过编程语言就能做,其考核思维、逻辑、编码能力。而这种题有“模拟题、构造题、思维题、找规律题”,统称“杂题”,每次蓝桥杯都会出现,而且可能有好几题,是重要的得分点!这些题可能比较简单,也可能比较难。下面就让我们一起来看看。
二、例题1——修剪灌木
修剪灌木 2022 年第十三届省赛, lanqiao0J 题号 2107
【问题描述】
爱丽丝要完成一项修剪灌木的工作。有 N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木。当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。灌木每天从早上到傍晚会长高 1 厘米,而其余时间不会长高。在第一天的早晨,所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高?
【输入格式】一个正整数 N,含义如题面所述。
【输出格式】输出 N 行,每行一个整数,第 i 行表示从左到右第 i 棵树最高能长到多高。
【评测用例规模与约定】对于30%的数据,N < 10;对于100%的数据,1 < N < 10000。

注意上面的循环是 0 ~ n-1。
三、例题2—— 付账问题
付账问题 2018年第九届蓝桥杯省赛,lanqiao0J 题号174
【题目描述】
有 n 个人出去吃饭,他们总共消费了 S 元。其中第 i 个人带了 ai 元。所有人带的钱的总数是足够付账的。
现在问题来了:每个人分别要出多少钱呢?
为了公平起见,我们希望在总付钱量恰好为 S 的前提下,最后每个人付的钱的标准差最小。
我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 1 分钱的整数倍。你需要输出最小的标准差是多少。
标准差:是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的“偏差有多大”。设第 i 个人付的钱为 bi 元,那么标准差为:
解题思路:
如果每人带的钱够多,人均完全一样,bi = S/n = avg,那就简单了,得 X = 0。不过总有人钱不够,分两种情况讨论:
(1)第 i 人带的钱不够平均数 avg,他只能出他带的全部钱 ai。
(2)第 i 人带的钱比平均数 avg 多,他可以多摊一些。
求解步骤:
(1)对 ai 从小到大排序;
(2)前一部分人的钱不够,那么就出他们所有的钱;
(3)从总付钱数中扣除前一部分人出的钱,得剩余钱数为S',以及后一部分人的出钱平均数avg' 。
(4)后一部分人的钱多,他们多出一些。怎么出?这部分人也分两类:
(i)比较有钱的,但是他的的钱还是要全出
(ii)非常有钱的,不管怎么摊他都有富余

from math import *
n,s=map(int,input().split())
a=list(map(int,input().split()))
a.sort()
avg=s/n
sum=0
for i in range(n):
if a[i]*(n-i)<s:
sum+=pow(a[i]-avg,2)
s-=a[i]
else:
cur_avg=s/(n-i) # 更新平均出线
sum+=pow(cur_avg-avg,2)*(n-i)
break
print("{:.4f}".format(sqrt(sum/(n))))
10 30
2 1 4 7 4 8 3 6 4 7
0.7928
>>> 四、例题3——最少砝码
最少砝码 2021年第十二届蓝桥杯省赛,lanqiao0J题号1461
【问题描述】
你有一架天平。现在你要设计一套砝码,使得利用这些砝码可以称出任意小于等于 N 的正整数重量。那么这套砝码最少需要包含多少个砝码?注意砝码可以放在天平两边。
【输入格式】
输入一行包含一个正整数 N,1 < N < 10^9。
【输出格式】
输出一行表示答案。
这他喵是一道规律题,有点意思的!
注意看下面的分析,学到了学到了。这个分析方法我不看答案确实没想出来。

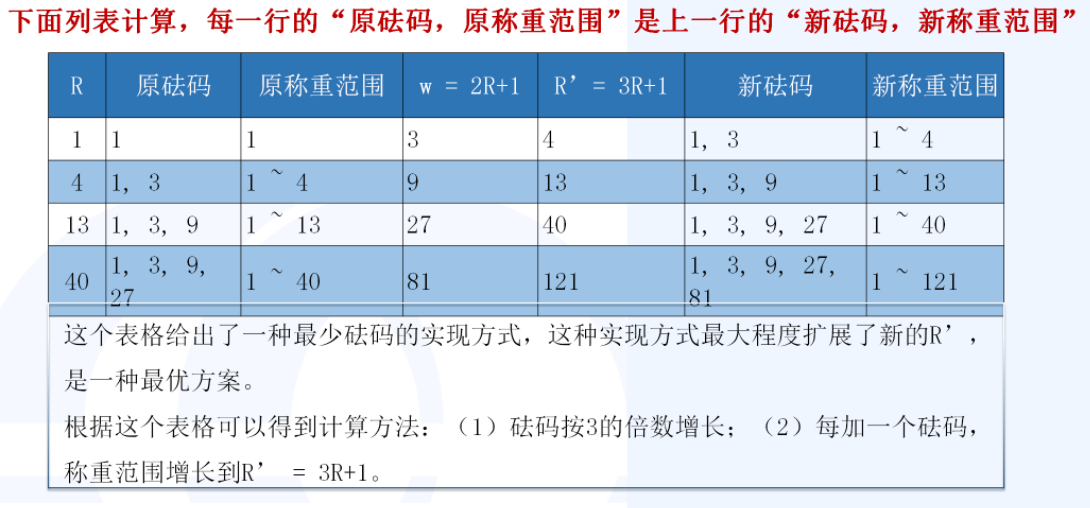
发现规律了吧!代码炒鸡简洁!
N=int(input())
R=1
cnt=1
while R<N:
R=R*3+1
cnt+=1
print(cnt)五、例题四——矩形拼接
矩形拼接 2022年第十三届省赛,lanqia00J 题号 2238
时间限制:1.0 s 内存限制:512.0 MB
【问题描述】
已知 3 个矩形的大小依次是 a1 × b1,a2 × b2 和 a3 × b3。用这 3 个矩形能拼出的所有多边形中,边数最少可以是多少?
解题思路:
本题是一道纯粹的构造题,思维简单,但是代码比较繁琐细致,目的是考核编码能力
3个矩形摆在一起,可能有几个边?在纸上手画观察,如果3个矩形完全不能匹配,是8边形;如果能完全匹配成一个新矩形,是4边形;其他情况是6边形。
本题只有3个矩形,并不复杂。3个矩形做任意组合,每个矩形有横竖两种摆法,共48种情况。T=1000组测试,总计算量是1000×48,计算量很小不会超时,所以简单地用暴力法组合出所有情况,取最小值即可。
def check1(x1,x2,x3):
if x1>=x2 and x1>=x3:
if x1==x2+x3 and a[2]+a[3]-x2==a[4]+a[5]-x3:
return True
if x2>=x1 and x2>=x3:
if x2==x1+x3 and a[0]+a[1]-x1==a[4]+a[5]-x3:
return True
if x3>=x1 and x3>=x2:
if x3==x1+x2 and a[0]+a[1]-x1==a[2]+a[3]-x2:
return True
def check2(x1,x2,x3):
if x1>=x2 and x1>=x3:
if x1==x2+x3:
return True
if x2>=x1 and x2>=x3:
if x2==x1+x3:
return True
if x3>=x1 and x3>=x2:
if x3==x1+x2:
return True
return False
T=int(input())
for t in range(T):
a=list(map(int,input().split()))
ans=8
for i in range(0,2): # 第一个矩形
for j in range(2,4): # 第二个矩形
for k in range(4,6): # 第三个矩形
x1,x2,x3 = a[i],a[j],a[k]
if x1==x2 and x2 == x3:
ans = min(ans,4)
if check1(x1,x2,x3):
ans = min(ans,4)
if x1==x2 or x1==x3 or x2==x3:
ans = min(ans,6)
if check2(x1,x2,x3):
ans = min(ans,6)
print(ans)
六、例题五——蜂巢
蜂巢 2022 年第十三届省赛, lanqiao0J 题号 2134
时间限制:1.0 s 内存限制:512.0 MB
【问题描述】
蜂巢由大量的六边形拼接而成,定义蜂巢中的方向为:
0 表示正西方向,1 表示西偏北 60°,2 表示东偏北 60°,3 表示正东,4 表示东偏南 60°,5 表示西偏南 60°。
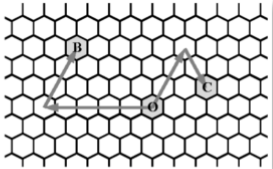
对于给定的一点 0,我们以 0 为原点定义坐标系,如果一个点 A 由 0 点先向 d 方向走 p 步再向 (d +2) mod 6 方向 ( d 的顺时针 120° 方向) 走 q 步到达,则这个点的坐标定义为 (d, p,q) 。
在蜂窝中,一个点的坐标可能有多种。上图给出了点 B(0, 5, 3) 和点 C(2, 3, 2) 的示意。给定点 (d1, p1, q1) 和点 (d2, p2, q2) ,请问他们之间最少走多少步可以到达?
这里定义了 “蜂巢坐标系”,故是要斜着走!


xdir = [-2,-1,1,2,1,-1]
ydir = [0,1,1,0,-1,-1]
def walk(d,q,x,y):
x += xdir[d]*q
y += ydir[d]*q
return x,y
d1,p1,q1,d2,p2,q2=map(int,input().split())
x1,y1 = walk(d1,p1,0,0)
x1,y1 = walk((d1+2)%6,q1,x1,y1)
x2,y2 = walk(d2,p2,0,0)
x2,y2 = walk((d2+2)%6,q2,x2,y2)
dx,dy = abs(x1-x2),abs(y1-y2)
if dx>=dy:
print((dx+dy)//2) # 先横着走,再斜着走,这公式是要推理出来的
else:
print(dy) # 一直斜着走
以上,Python杂题
祝好