翻译:
给定一个数组𝑎1,𝑎2,…,𝑎𝑛,由𝑛个正整数组成。
最初,您位于索引1,分数等于𝑎1。你可以执行两种动作:
向右移动-从您当前的索引𝑥到𝑥+1,并将𝑎𝑥+1添加到您的分数。只有当𝑥<𝑛时才能执行此移动。
向左移动-从当前索引𝑥到𝑥−1,并将𝑎𝑥−1添加到您的分数中。𝑥>1.单击“确定”。此外,你不能在一行中向左移动两次或两次以上。
您希望执行精确的𝑘动作。此外,其中向左移动的次数不应超过𝑧次。
你能得的最高分是多少?
输入
第一行包含一个整数𝑡(1≤𝑡≤104)——测试用例的数量。
每个测试用例的第一行包含三个整数𝑛、𝑘和𝑧(2≤𝑛≤105,1≤𝑘≤𝑛−1,0≤𝑧≤𝑚𝑖𝑛(5,𝑘))-数组中的元素数量,应该执行的总移动次数和可以执行的最大向左移动次数。
每个测试用例的第二行包含𝑛整数𝑎1,𝑎2,…,𝑎𝑛(1≤𝑎𝑖≤104)-给定数组。
𝑛对所有测试用例的和不超过3⋅105。
输出
打印𝑡个整数——对于每个测试用例输出的最大分数,如果你总共移动了𝑘次,向左移动的不超过𝑧次,并且在一行中没有两次或两次以上向左移动。
例子
inputCopy
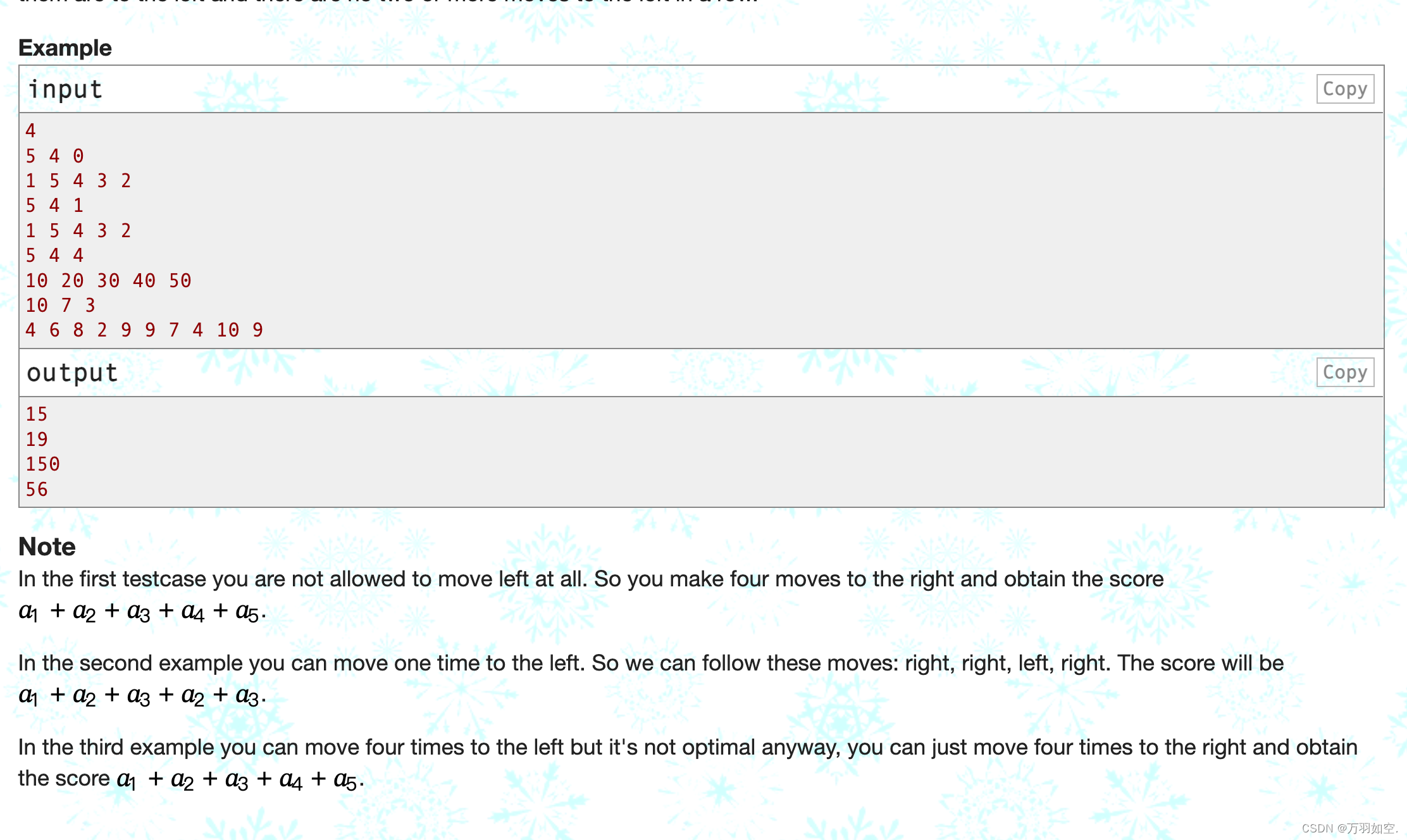
4
5 4 0
1 5 4 3 2
5 4 1
1 5 4 3 2
5 4 4
10 20 30 40 50
10 7 3
4 6 8 2 9 9 7 4 10 9
outputCopy
15
19
150
56
请注意
在第一个测试用例中,您根本不允许向左移动。所以你向右移动四步,得到分数𝑎1+𝑎2+𝑎3+𝑎4+𝑎5。
在第二个例子中,你可以向左移动一次。所以我们可以跟着这些动作:右,右,左,右。分数将是𝑎1+𝑎2+𝑎3+𝑎2+𝑎3。
在第三个例子中,你可以向左移动四次,但这不是最优的,你可以向右移动四次,得到分数𝑎1+𝑎2+𝑎3+𝑎4+𝑎5。
思路:
不可以连续向左走,而且向左回头有次数限制,所以我们只需要考虑连续的两个最大值,然后我们判断,当前向左回头,与总步数,可以进行多少次,然后来判断最值。
代码:
/*Looking! The blitz loop this planet to search way
Only my RAILGUN can shoot it 今すぐ
身体中を 光の速さで
駆け巡った確かな予感
掴め! 望むものなら残さず
輝ける自分らしさで
信じてるよ あの日の誓いを
この瞳に光る涙それさえも 強さになるから
*/
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long ll;
int n,t;
inline __int128 read(){
__int128 x = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){
if(ch == '-')
f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9'){
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
inline void print(__int128 x){
if(x < 0){
putchar('-');
x = -x;
}
if(x > 9)
print(x / 10);
putchar(x % 10 + '0');
}
int k,z;
ll a[100005];
void wanyurukong(){
cin>>n>>k>>z;
for (int i =1; i<=n; i++) {
cin>>a[i];
}
ll sum=0;
ll fs=-1;
ll ans=-1;
ll jk=-1;
for (int i =1; i<=k+1; i++) {
sum+=a[i];
fs=max(fs,a[i+1]+a[i]);
ans=max(ans,sum+min(z,(k-i+1)/2)*fs);
}
printf("%lld\n",ans);
}
int main(){
ios::sync_with_stdio(false);
cin.tie(); cout.tie();
cin>>t;
while (t--) {
wanyurukong();
}
//wanyurukong
return 0;
}