个人博客
- 密码技术扫盲,Part 1:对称加密
- 密码技术扫盲,Part 2:非对称加密
- 🎯 密码技术扫盲,Part 3:认证
除了加密,还有一类用法是对信息的认证,主要包括 4 个技术
- 单向散列,计算 Hash 值
- 消息认证码,单向散列+密钥
- 数字签名,单向散列+私钥
- 证书,参见之前写的一篇《Web 安全,Part 1:PKI 扫盲》
单向散列
单向散列就是哈希函数,用于计算消息/文件的特征,可以类比于人的指纹,如果消息发生了一个比特的变化,那么计算出的散列值也不同(存在散列值相同的不同消息,但非常难找到这样的两条,称为碰撞),这让消息的接收者可以验证消息是否发生了损坏或者被篡改,保障了消息的完整性。
从原文可以计算得到散列值,但从散列值无法还原得到原文,所以称单向散列。
无论输入有多大,散列函数的输出长度都是固定的,如 SHA-256 总是输出长度为 256 位的散列值。
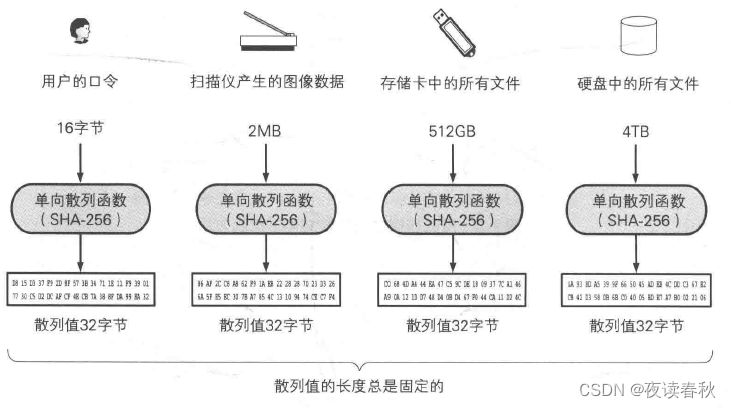
常用的单向散列函数如下,其中 SHA 系列都是美国 NIST 制定的:
- MD4,计算出 128 位的散列值,不安全
- MD5,计算出 128 位的散列值,不安全
- SM3,计算出 256 位的散列值,安全,国内搞出来的商密标准散列函数
- SHA-1,计算出 160 位的散列值,不安全
- SHA-2,包括 2 个基础版本(SHA-256、SHA-512)及 4 个衍生版本
- SHA-224,将 SHA-256 的结果截掉 32 位
- SHA-256,计算出 256 位的散列值,安全,比较常用
- SHA-512/224,将 SHA-512 的结果截掉 288 位
- SHA-512/256,将 SHA-512 的结果截掉 256 位
- SHA-384,将 SHA-512 的结果截掉 128 位
- SHA-512,计算出 512 位的散列值,安全,比较常用
- SHA-3,和 AES 相似,也是采用全球公开选拔的方式,最终胜者为 Keccak 算法,包含 4 种输出长度版本
- SHA3-224,计算出 224 位的散列值
- SHA3-256,计算出 256 位的散列值
- SHA3-384,计算出 384 位的散列值
- SHA3-512,计算出 512 位的散列值
一般我们在互联网上下载软件时,官方网站会同时提供散列值,可以验证软件是否完整。
单向散列虽然能保障完整性,保障消息/文件没有被篡改,但却不能防止伪装。假设恶意攻击者攻击了某软件的下载页面,同时将软件和散列值都进行了替换,普通用户是无法发现的。如果想要识别出这种伪装,就需要用到消息认证码和数字签名技术。
消息认证码
MAC(Message Authentication Code),消息认证码也是在计算散列值,但计算过程需要用到一个密钥,有了密钥的加入,就可以确认消息是持有密钥的某一方发的——除非密钥泄露。
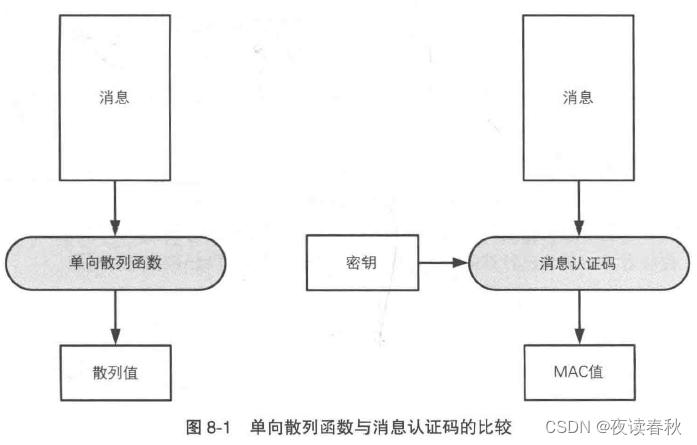
消息认证码的主要实现方式:
- 使用单向散列函数,称为 HMAC,根据单向散列函数的不同,又有若干种组合
- HMAC-SHA1
- HMAC-SHA224
- HMAC-SHA256
- HMAC-SHA512
- HMAC-SM3
- …
- 使用分组密码
- 使用流密码
- 使用公钥密码
HMAC 方式用得较多,包括在 TLS 中很多协商组合也多是用 SHA 系列来计算 MAC。
大名鼎鼎的 SWIFT(Society for Worldwide Interbank Financial Telecommunication) 系统在银行间传递消息时就用到了消息认证码技术 —— 这组织牛到当初俄乌战争爆发,西方国家威胁要把俄罗斯踢出 SWIFT 系统,坊间称之为金融核弹级别的制裁措施。从技术角度来说,消息认证码在其中的使用方式大略如下图所示
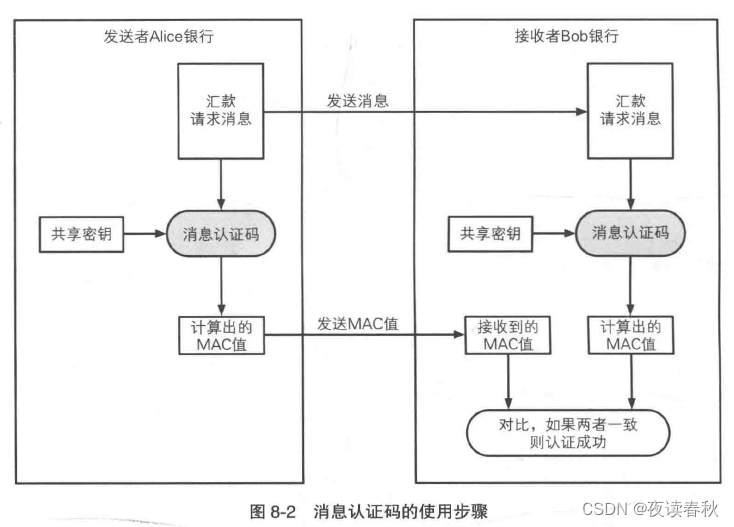
在规避重放攻击时,可以选择使用消息序号、时间戳、nonce 等技术。
消息认证码虽然解决了伪装的问题,但因为密钥是在所有参与方之间共享的,所以无法防止抵赖问题,如对于一笔转账,一方完全可以耍赖说是其他知道密钥的几方做的,从该项技术上无法证伪。
数字签名
既然共享密钥会带来抵赖问题,那是否可以不共享密钥?
回忆一下,在介绍非对称加密技术时,我们学习了公钥、私钥组成的公钥密码系统,在加密时,我们采用公开的公钥加密原文,这样密文就只有持有不公开的私钥的持有者可以解密,保障了信息传递的机密性,开辟了解决密钥配送问题的一种新思路。
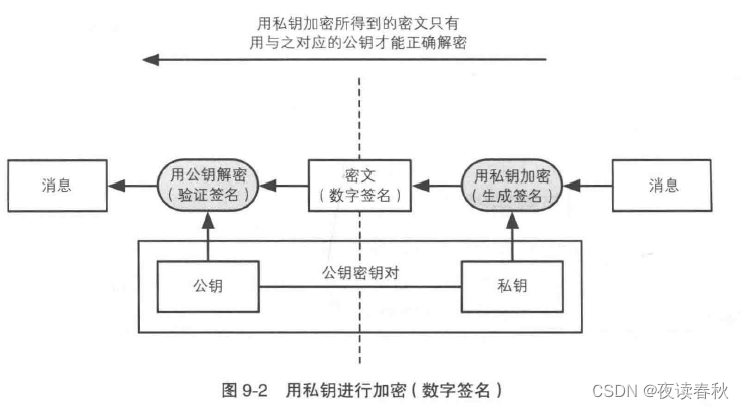
现在我们反过来想,如果用公钥能解开一段密文,那就可以证明这段密文是用对应的私钥加密的,因为私钥是不公开的,继而可以确认这段密文是私钥持有者操作生成的,这段加密的信息就是数字签名。这里私钥就成为了电子身份的锚点,进一步延伸就触及到我们之前介绍过的 PKI 体系。
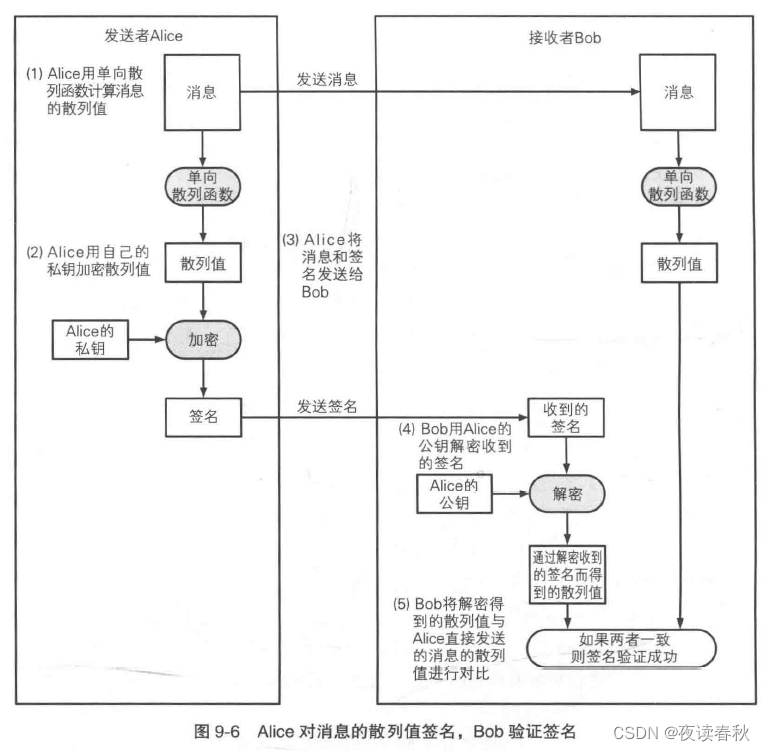
在实际使用中,并不会直接使用传递的消息来生成数字签名,而是使用传递消息的单向散列值来生成数字签名。
除了公钥密码的 RSA,也存在其他几种签名方法:ElGamal、DSA、ECDSA、Rabin,不继续展开。
补充一个数字信封技术:用申请组织的公钥来加密对称密钥后得到的密文,其中对称密钥被用于加密信封里的信息。
参考:
- 《图解密码技术》