tips:B-树读成b树,并不是b减树
【一】基本搜索结构
| 种类 | 数据格式 | 时间复杂度 |
| 顺序查找 | 无要求 | O(N) |
| 二分查找 | 有序 | O(log2N) |
| 二叉搜索树 | 无要求 | O(N) |
| 二叉平衡树(AVL和红黑树) | 无要求,最后随机 | O(log2N) |
| 哈希 | 无要求 | O(1) |
| 位图 | 无要求 | O(1) |
| 布隆过滤器 | 无要求 | O(k)(k为哈希函数个数,一般比较小) |
以上结构适合于数据量不是很大的情况下,如果数据量是非常大的,一次无法加载到内存中,使用上述结构就不是很方便,需要多次IO。
【二】使用平衡树搜索一个大文件
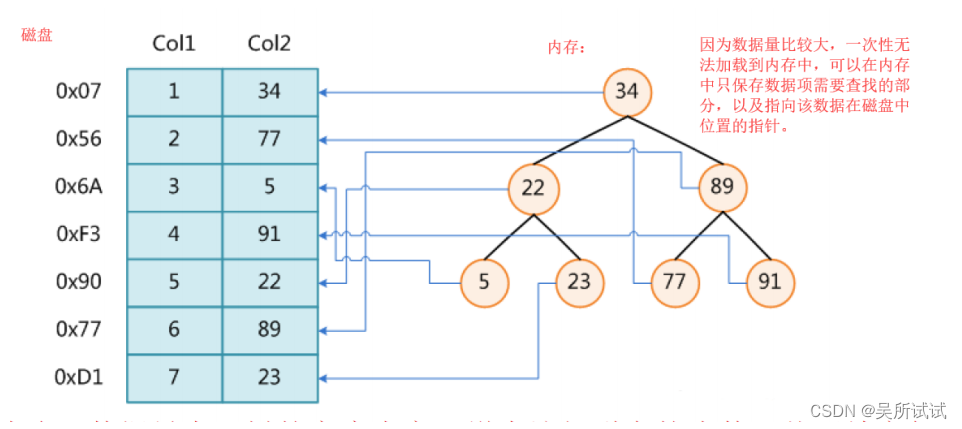
上述方式只是在内存中保存了每一项数据信息中需要查找的字段在磁盘中的位置,整体的数据实际上在磁盘中:
缺陷:
1.树的高度比较高,查找时最差的情况下要比较树的高度次
2.数据量如果特别大时,树中的节点可能无法一次性加载到内存中,需要多次IO
如何加速对数据的访问呢?
1.提高IO的速度
2.降低树的高度---平衡多茶树
【三】B-树概念
一颗M(M>2)的B树,是一颗平衡的M路平衡搜索树,可以是空树或者满足以下性质:
1.根节点至少有两个孩子
2.每个根节点至少有m/2-1个关键字,至多有m-1个关键字,并且以升序排列
3.每个非根节点至少有m/2个孩子,至多有m个孩子
4.key[i]和key[i+1]之间的孩子节点的值介于key[i],key[i+1]之间
5.所有的叶子节点都在同一层
【四】B-树的结构分析
为了简单起见,假设M=3,即是三叉树,每个节点之中存储两个数据,两个数据可以区分成三个部分,因此节点应该有三个孩子,为了后续实现简单期间,节点的结构如下:
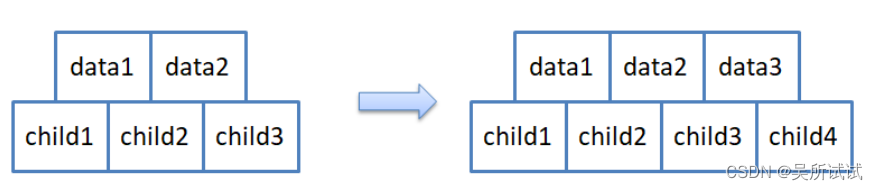
注意:孩子永远比数据多一个
【五】插入过程分析
1.如果树为空,直接插入新节点中,该节点为树的根节点
2.树非空,找待插入元素在树中的插入位置(注意:找到的插入节点位置一定在叶子节点中)
3.检测是否找到插入位置(假设树种key的位置唯一,也就是这个元素存在的适合不插入)
4.按照插入排序的思想将该元素插入到找到的节点中
5.检测该节点是否满足B-树的性质:即该节点中的元素个数是否等于M,如果小于则满足
6.如果插入后节点不满足B-树的性质,则需要对该节点进行分裂
a.申请新节点
b.找到该节点的中间位置
c.将该节点中间位置右侧元素及其孩子节点搬运到新节点中
d.将中间位置以及新节点往该节点的双亲节点中插入,也就是继续4的操作
7如果向上分裂到根节点的位置,插入结束
【六】B-树的性能分析
对于一颗节点为N度为M的B-树,查找和插入需要logM-1N次进行比较,这个还是比较好证明:对于度为M的B-树,每一个节点的个数为M/2~(M-1)之间,因此树的高度应该要在logM-1和logM/2N之间,在定位到该节点之后,使用二分查找就可以定位到元素,知道为什么在这里能进行二分查找吗?因为我们插入的时候,是按照大小进行插入,分裂的时候也是按照大小进行分裂的。所以存入的一定是有序的数据,所以可以使用二分查找。
B-树的效率是很高的,对于N = 62*1000000000个节点,如果度M为1024,则 <= 4,即在620亿个元素 中,如果这棵树的度为1024,则需要小于4次即可定位到该节点,然后利用二分查找可以快速定位到该元素,大大 减少了读取磁盘的次数。
以上就是这期B-树的全部内容了,有问题的地方还请打架位于评论区进行斧正,如果觉得还行,还请一件三连,毕竟码字不易。