实验5—— 基于随机二进制树的防冲突算法的实现与性能分析
实验说明: 利用Python或Matlab模拟基于随机二进制树的防冲突算法; 分析标签数量k对遍历所有标签所需时间的影响; 分析标签ID的长度、分布对算法性能的影响; 利用Python或Matlab画出相应的曲线,并分析算法的优缺点。
queryBinaryTree.py:
import random
from task5_randomBinary.Tag import Tag
import numpy as np
import matplotlib.pyplot as plt
font3 = {
'family': 'SimHei',
'weight': 'normal',
'size': 20,
}
def cal(tagNum, idLen):
"""
function: 计算标签数量和标签id长度对数据发送的影响
:param tagNum: 标签数量
:param idLen: 标签id长度
:return:
"""
tagList = []
vis = []
for i in range(tagNum):
tag = Tag()
strs = ''
for j in range(idLen):
t = random.randint(0, 1)
strs += str(t)
tag.id = strs
tagList.append(tag)
vis.append(False)
# print(i, strs)
stack = []
strs = ''
flag = 0
cntSum = 0
index = []
cnt1 = 0 # 作为标志位
while 1:
cntSum += 1
if cnt1 == 0:
strs += '0'
stack.append(1)
else:
strs = strs[0:-1] #pop掉最后一个元素
if len(stack) == 0:
return cntSum
t = stack.pop()
strs += str(t)
cnt0 = 0
for i in range(tagNum):
if tagList[i].id[0:len(strs)] == strs:
cnt0 += 1 # 前缀id匹配的标签数量 即冲突数量
index.append(i)
if cnt0 == 0: # 空时隙
cnt1 = 1
elif cnt0 == 1: # 未冲突且刚好匹配
flag += 1
vis[index[0]] = True
cnt1 = 1
else: # 为冲突时隙
cnt1 = 0
if len(strs) == idLen and cnt0 > 1:
for j in index:
vis[j] = True
flag += 1
if flag == tagNum:
return cntSum
def main():
tagNum = 250
idLen = 300
print('-------标签数量k对发送完所有标签时间的影响---------')
ratio = []
for i in range(1, tagNum):
rate = []
for j in range(3):
t = cal(i, 10) # 控制变量,默认所有标签的id长度为5
rate.append(t)
ratio.append(np.average(rate))
print(i, ratio[i-1])
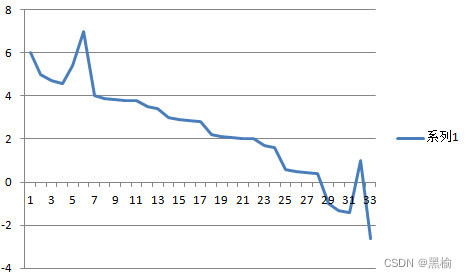
plt.plot(np.arange(1, tagNum), ratio, color='b', linestyle='-', marker='*', linewidth=2.0)
plt.xlabel('标签数量', font3)
plt.ylabel('h发送完所有标签所需要的时间', font3)
plt.show()
print('-------标签长度对发送完所有标签时间的影响---------')
ratio.clear()
for i in range(5, idLen):
rate = []
for j in range(3):
t = cal(10, i) # 控制变量,默认标签数量为10
rate.append(t)
ratio.append(np.average(rate))
plt.plot(np.arange(5, idLen), ratio, color='g', linestyle='-', marker='*', linewidth=2.0)
plt.xlabel('标签的id长度', font3)
plt.ylabel('h发送完所有标签所需要的时间', font3)
plt.show()
if __name__ == '__main__':
main()randomBinaryTree.py:
"""
1.利用Python或Matlab模拟基于随机二进制树的防冲突算法;
2.分析标签数量k对遍历所有标签所需时间的影响;
3.分析标签ID的长度、分布对算法性能的影响;
4.利用Python或Matlab画出相应的曲线,并分析算法的优缺点。
"""
import random
from task5_randomBinary.Tag import Tag
import matplotlib.pyplot as plt
import numpy as np
font3 = {'family': 'SimHei',
'weight': 'normal',
'size': 20,
}
def cal(tagNum, idLen):
"""
function: 计算标签数量k对遍历所有标签所需时间的影响;分析标签ID的长度、分布对算法性能的影响
:param tagNum:标签数量
:return:所需时间
"""
tagList = []
for i in range(tagNum):
tag = Tag()
tag.slot = random.randint(0, 1) # 跳过初始化为0的阶段,默认全部冲突,在0和1中随机选择一个数
idStr = ''
for j in range(idLen):
t = random.randint(0, 9)
idStr += str(t)
tag.id = idStr
tagList.append(tag)
# for i in range(tagNum):
# print(tagNum, tagList[i].slot, tagList[i].id)
flag = 0 # 计数成功发送的标签个数
cnt = 0 # 遍历所有标签所需时间
index0 = [] # 用于计数此刻多少个标签slot为0
index1 = [] # 用于计数此刻多少个标签slot为1
index2 = [] # 用于计数此刻多少个标签slot>1
while 1:
index0.clear()
index1.clear()
index2.clear()
cnt += 1
t = None
for i in range(tagNum):
if not tagList[i].isSubmerge: # 表明标签还没有沉默
# print('coming')
if tagList[i].slot == 0:
index0.append(i)
elif tagList[i].slot == 1:
index1.append(i)
elif tagList[i].slot > 1:
index2.append(i)
# print(len(index0), len(index1), len(index2))
if len(index0) == 0: # 表明为空时隙
t = -1
elif len(index0) == 1: # 表明为单时隙不冲突
# print('标签{}成功发送数据'.format(tagList[index0[0]].id))
tagList[index0[0]].isSubmerge = True
flag += 1
if flag == tagNum:
return cnt
t = -1
else: # 表明为冲突时隙
for j in index0:
# print(j, end=' ')
tagList[j].slot = random.randint(0, 1)
t = 1
# print('\n')
for j in index1:
tagList[j].slot += t
for j in index2:
tagList[j].slot += t
def main():
tagNum = 250
idLength = 1000
ratio = []
print('----------标签数量k对遍历所有标签所需时间的影响----------')
for i in range(1, tagNum):
rate = []
for j in range(3):
t = cal(i, 4)
rate.append(t)
ratio.append(np.average(rate))
print(i, ratio[i-1])
plt.plot(np.arange(1, tagNum), ratio, color='g', linestyle='-', marker='*', linewidth=2.0)
plt.xlabel('标签数量', font3)
plt.ylabel('发送完所有标签所需要的时间', font3)
plt.show()
print('----------标签数量k对遍历所有标签所需时间的影响----------')
ratio.clear()
for i in range(1, idLength):
rate = []
for j in range(3):
t = cal(10, i)
rate.append(t)
ratio.append(np.average(rate))
print(i, ratio[i-1])
plt.plot(np.arange(1, idLength), ratio, color='b', linestyle='-', marker='*', linewidth=2.0)
plt.xlabel('标签ID的长度、分布', font3)
plt.ylabel('发送完所有标签所需要的时间', font3)
plt.show()
if __name__ == '__main__':
main()基于二进制树的防冲突算法
基本思想:按照递归的方式将冲突的标签集合划分为两个子集,直到集合中只剩下一个标签为止。划分子集的算法有两种:
- 让标签随机选择所属的集合——随机二进制树算法
- 按照标签的标识符划分子集——查询二进制树算法
基于随机二进制树的防冲突算法:
- 随机二进制树算法需要每个标签维持一个计数器,计数器初始值为0。
- 在每一个时隙开始时,如果标签的计数器为0时,则立即发送自己的标识符,否则该时隙不响应。
- 一般标签被成功识别,则该标签进入沉默状态,对以后时隙的阅读器不再响应。
- 因此,第一个时隙的所有标签都会回复,因为它们的计数器此时都为0。
- 每一个时隙结束后阅读器会将自己接收到的时隙状态(冲突或者不冲突)反馈给标签,场内的标签根据反馈的结果对自己维持的计数器进行调整。
标签调整计数器的规则:
- 如果该时隙为冲突时隙,那么参与响应的标签就会从0或1两个数字中随机选择一个,将其加到自己的计数器上;没有参与响应的标签直接将自己的计数器加1。这样冲突的标签集合会被分为两个集合,一个选0的集合和一个选1的集合。
- 如果该时隙没有冲突发生,则表明该时隙为没有标签响应的空时隙或者是只有一个标签响应的单时隙。被成功识别的标签进入沉默状态,直到新的识别过程开始,而没有被成功识别的标签则将自己的计数器减一。阅读器重复以上过程,直到所有标签被识别为止。
- 整个识别过程就像一棵二叉树的中序遍历
- 随机二进制树算法,不存在标签饿死的问题。它通过不断地将产生冲突的标签集合划分为两个子集合,直到某一个集合中只有一个标签存在时,成功识别该标签。标签过程是随机的,只需要维持一个内部状态,即计数器
基于查询二进制树的防冲突算法:
- 查询二进制树算法是一个无状态协议,标签只需要根据阅读器广播的标识符前缀作比较,标签内部不需要维持任何状态。阅读器将维持一个二进制前缀,初始值为0。
- 每一个时隙开始时,阅读器广播该二进制前缀,标签将自己的标识符前几位与此二进制前缀进行比较,若相同则该标签发送标识符。否则标签保持沉默。
- 如果阅读器探测到有冲突发生,则在下次查询的时候将原来的二进制前缀后面加0或1,重新查询。
- 阅读器重复以上过程,直到识别完所有的标签。
- 整个标识过程就像是根据标签的标识符号建立一棵二叉树,又称为查询二叉树。
查询二进制树的协议的性能受标签标识符ID的长度以及分布的影响
参考链接:
(25条消息) 基于二进制树的防冲突算法_Caramel_biscuit的博客-CSDN博客_二进制树防碰撞算法







![[Python从零到壹] 六十一.图像识别及经典案例篇之基于纹理背景和聚类算法的图像分割](https://img-blog.csdnimg.cn/dbe8e250f7004ee1b3b120ae0974280c.png#pic_center)