目录
一、算法介绍
二、算法描述
三、算法总结
一、算法介绍
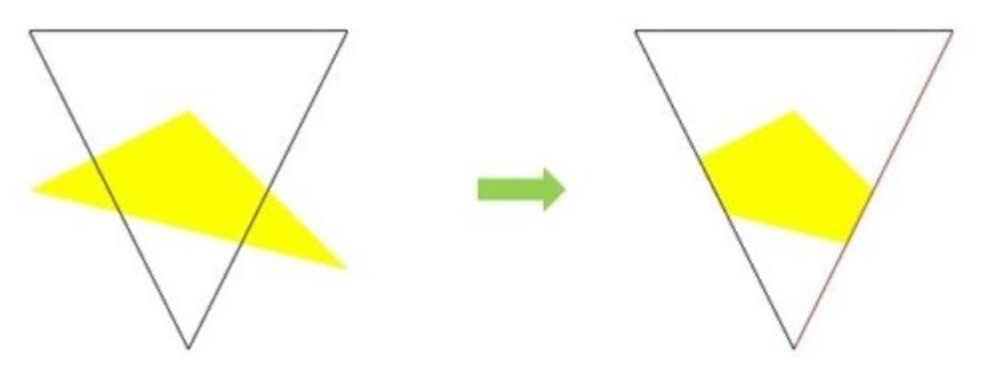
Weiler Atherton多边形裁剪算法是一种允许裁剪凹面算法的算法。与 Sutherland-Hodgman 多边形裁剪算法最主要的区别是,该算法能够裁剪凹多边形,并不留下任何残留物。
裁剪示意图:
二、算法描述
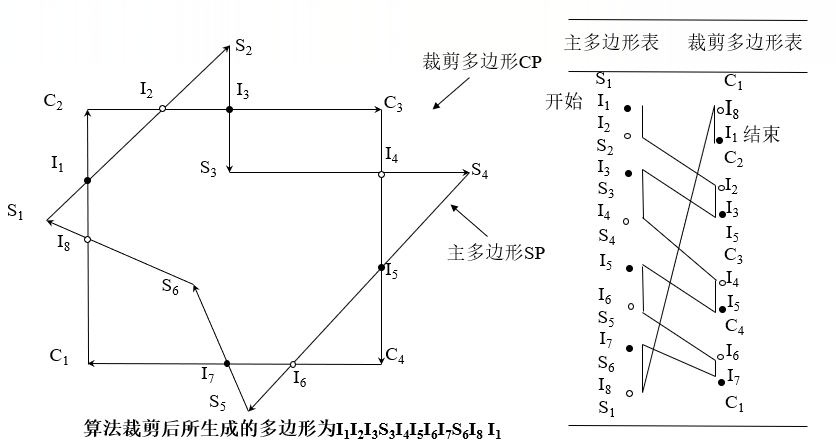
我们直接以下图举例,来描述使用Weiler-Atherton算法裁剪凹多边形的过程:
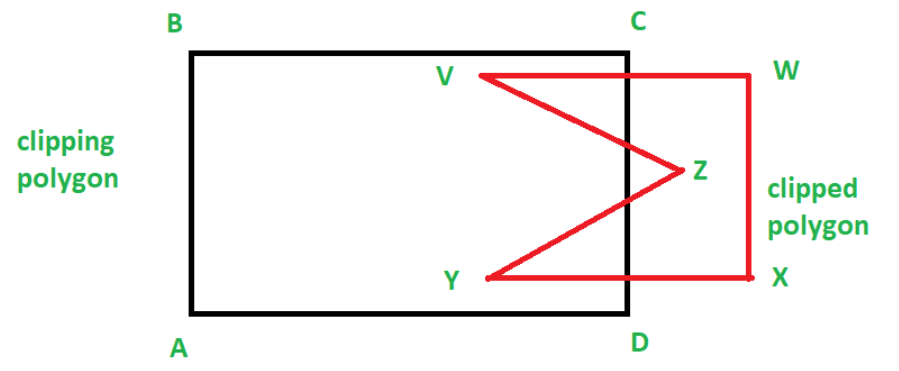
1、标记裁剪多边形和被裁剪多边形的交点,并判断进点与出点(判断方法具体参考Cyrus Beck算法)。
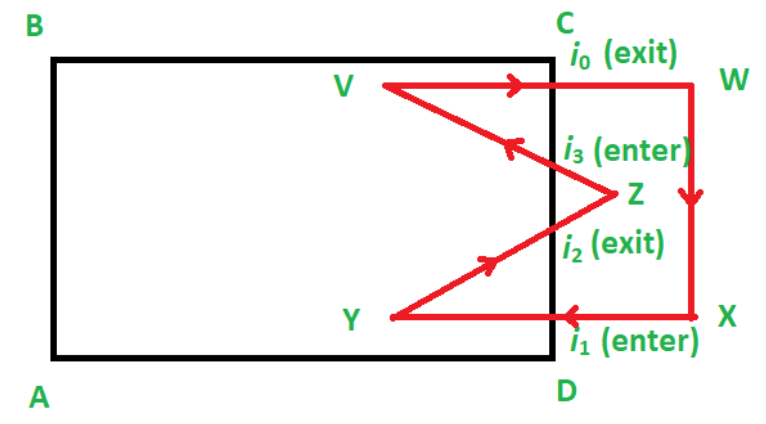
2、建立两个集合,分别存放被裁剪多边形的顶点和裁剪多边形的顶点。
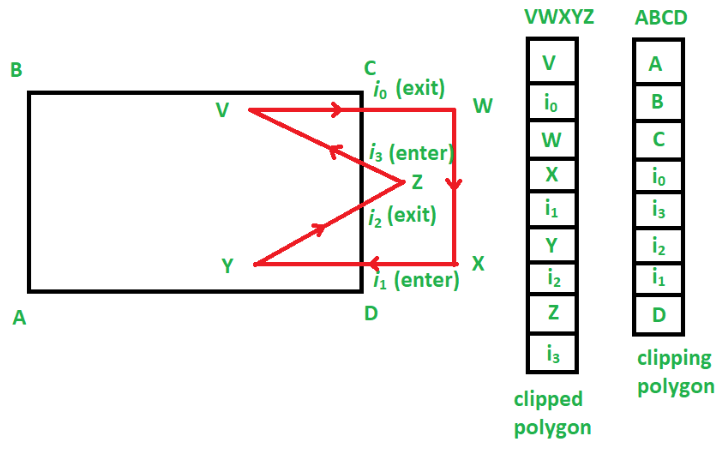
3、开始建立两个集合的联系。
我们首先访问任意一个进点,这里以 i1 举例。然后依次访问 Y点和i2点后退出:
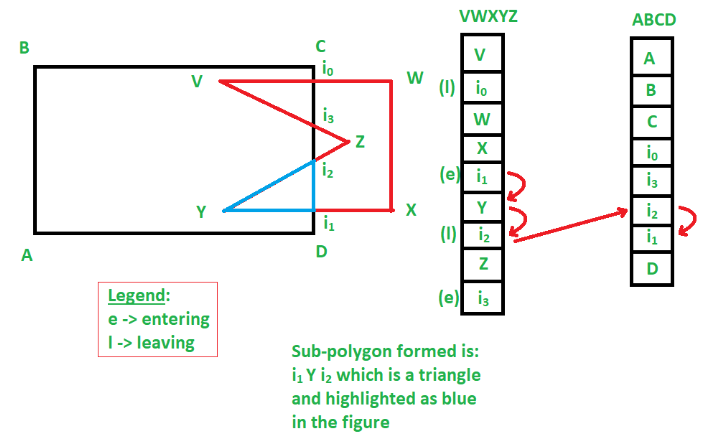
4、同理建立下一个联系:
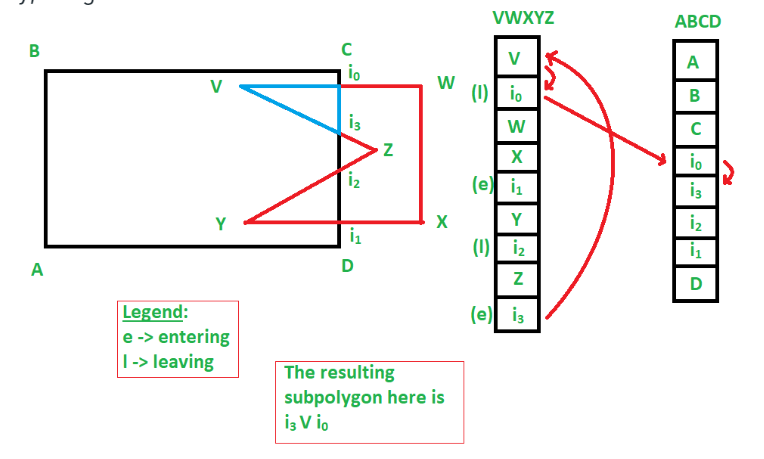
5、遍历集合,最终结果:
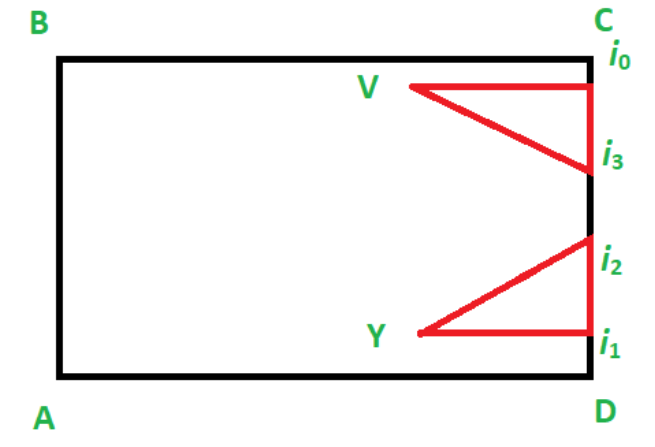
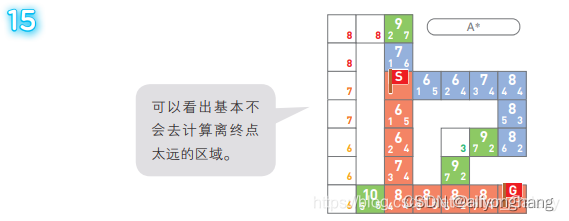
再补几幅图加深下印象ヽ(*^ー^)人(^ー^*)ノ

三、算法总结
Weiler Atherton多边形裁剪算法适用于凹、凸、带内环多边形,解决了Sutherland-Hodgman算法有残留的问题。不过Weiler Atherton算法对self-intersecting polygons(多边形自交)束手无策。