虽称为激活函数大全,但也不敢太过自满,如有遗漏与错误,还请指正
文章目录
- 线性激活函数
- Sigmoid 函数
- LogSigmoid
- Swish
- Tanh / 双曲正切激活函数
- TanhShrink
- Softsign
- ReLU 函数
- BReLU
- Leaky ReLU
- PReLU
- RReLU
- ELU
- SELU
- CELU
- GELU
- Softmax 函数
- Maxout 函数
- Softplus 函数
线性激活函数
f ( x ) = a x f ( x ) ∈ ( − ∞ , ∞ ) f(x)=ax\\f(x)\in(-\infin,\infin) f(x)=axf(x)∈(−∞,∞)
Sigmoid 函数
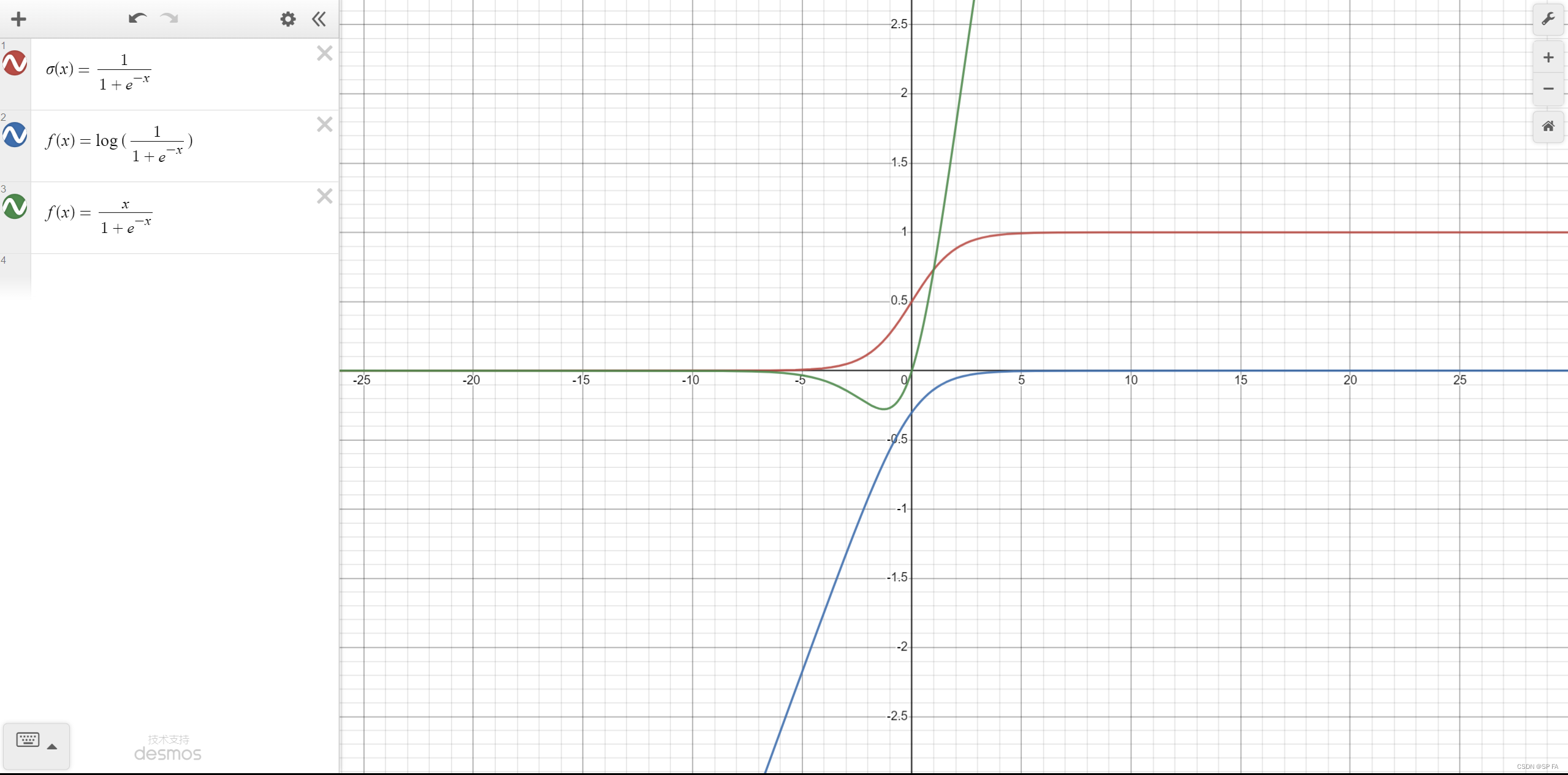
σ ( x ) = 1 1 + e − x \sigma(x)=\frac1{1+e^{-x}} σ(x)=1+e−x1优点:
- 对神经元的输出进行归一化
- 用于将预测概率作为输出的模型
- 梯度平滑
- 明确的预测,输出非常接近 1 或 0
缺点:
- 倾向于梯度消失
- 输出不是以 0 为中心,会降低权重更新效率
- 指数运算速度慢
LogSigmoid
f ( x ) = log ( 1 1 + e − x ) f(x)=\log(\frac1{1+e^{-x}}) f(x)=log(1+e−x1)
Swish
f ( x ) = x ∗ s i g m o i d ( x ) = x 1 + e − x f(x)=x*sigmoid(x)=\frac x{1+e^{-x}} f(x)=x∗sigmoid(x)=1+e−xxSwish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制,这称为 self-gating。
self-gating 的优点在于它只需要简单的标量输入,而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated激活函数能够轻松替换以单个标量为输入的激活函数(例如 ReLU),而无需更改隐藏容量或参数数量。
优点:
- 无界性有助于防止训练期间,梯度逐渐接近 0 并导致饱和(有界性也是有优势的,因为有界激活函数可以具有很强的正则化,并且较大的负输入问题也能解决)
- 导数恒 > 0 >0 >0
- 平滑度在优化和泛化中起了重要作用。
Tanh / 双曲正切激活函数
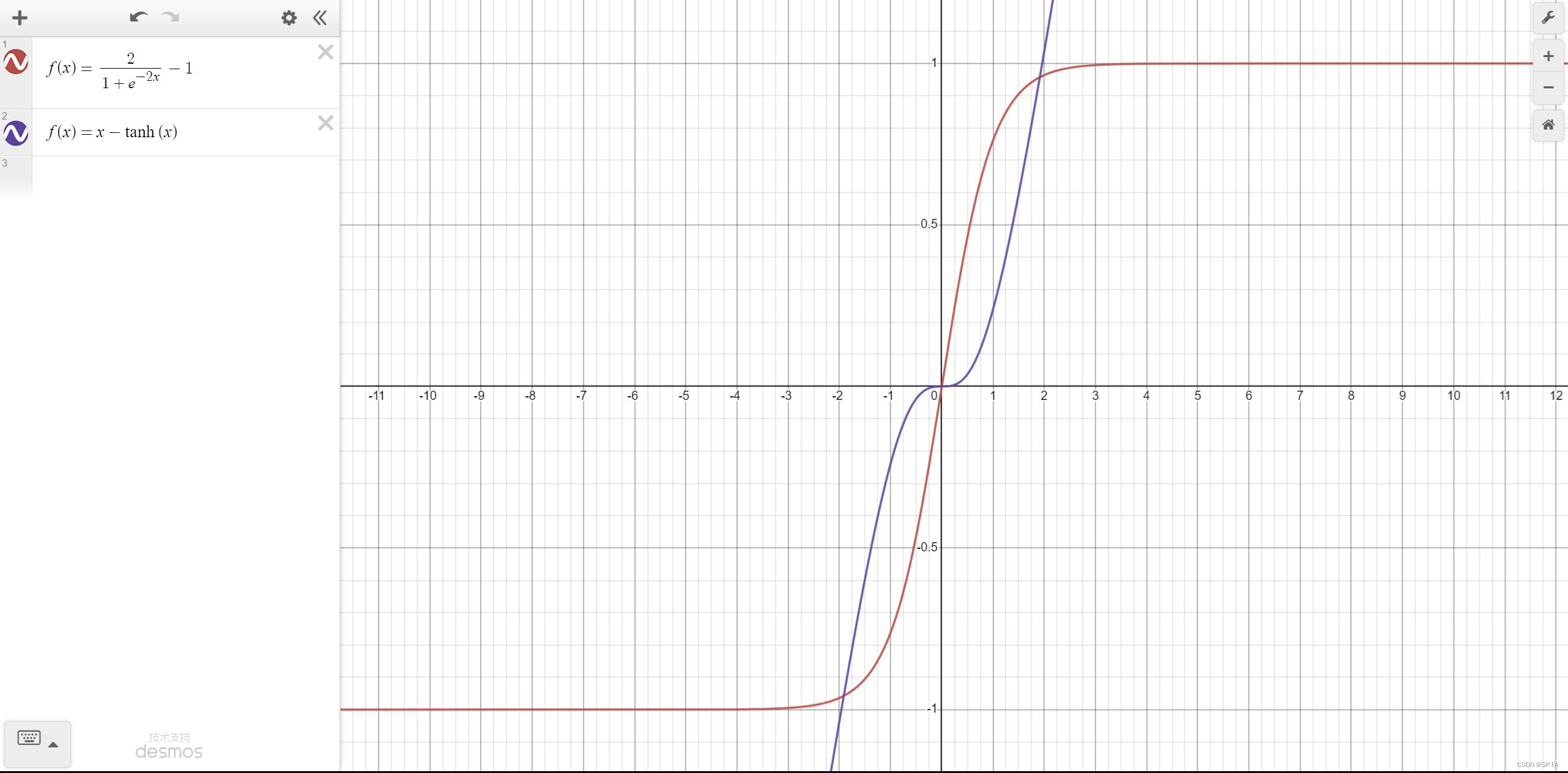
f ( x ) = t a n h ( x ) = 2 1 + e − 2 x − 1 f(x)=tanh(x)=\frac2{1+e^{-2x}}-1 f(x)=tanh(x)=1+e−2x2−1与 sigmoid 相比,它的优点就是以 0 为中心,收敛速度比 Sigmoid 快
一般在二分类问题中,tanh 用于隐藏层,而 sigmoid 用于输出层
TanhShrink
f
(
x
)
=
x
−
t
a
n
h
(
x
)
f(x)=x-tanh(x)
f(x)=x−tanh(x)
Softsign
f
(
x
)
=
x
1
+
∣
x
∣
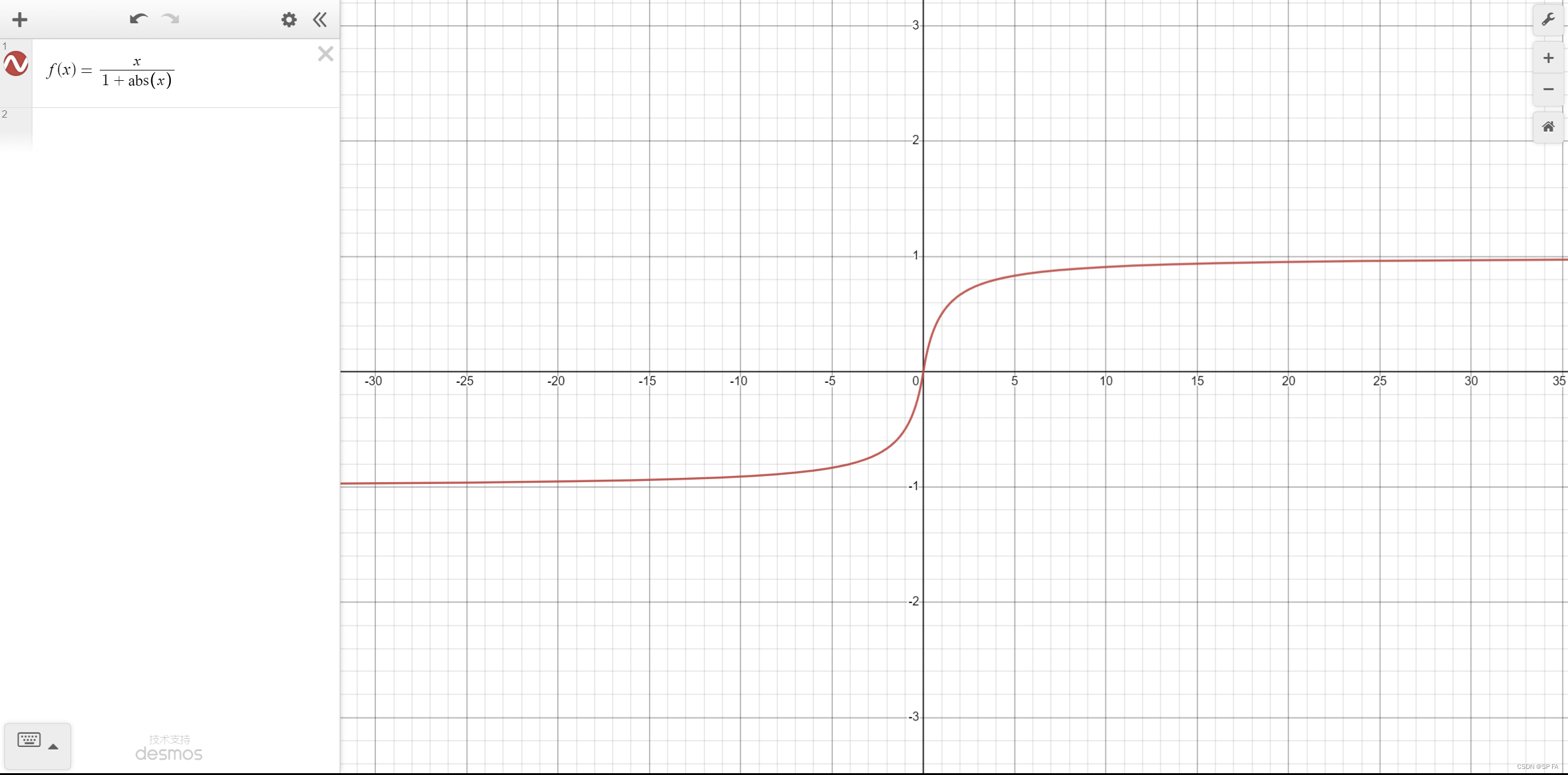
f(x)=\frac x{1+|x|}
f(x)=1+∣x∣xSoftsign 是 tanh 的一个替代选择,相比于tanh,Sotsign 的曲线更平坦,导数下降的更慢一点,这使得它可以缓解梯度消失问题,可以更高效的学习。
ReLU 函数
σ ( x ) = max ( 0 , x ) \sigma(x)=\max(0,x) σ(x)=max(0,x)优点:
- 当输入为正时,不存在梯度饱和问题
- 计算速度快
缺点:
- Dead ReLU 问题,当输入为负时 ReLU 失效。在正向传播过程中有些区域会很敏感,有些不敏感。但是在反向传播过程中,如果输入负数,则梯度完全为 0。
梯度饱和:
有些函数(如 Sigmoid 或 Tanh)自变量进入某个区间后,梯度会非常小,函数曲线越来越趋近一条水平直线。梯度饱和会导致训练过程中梯度变化缓慢,从而造成模型训练缓慢。梯度饱和是造成梯度消失的原因之一。
BReLU
限制 ReLU 的输出不超过 n n n。 f ( x ) = min ( max ( 0 , x ) , n ) f(x)=\min(\max(0,x),n) f(x)=min(max(0,x),n)
Leaky ReLU
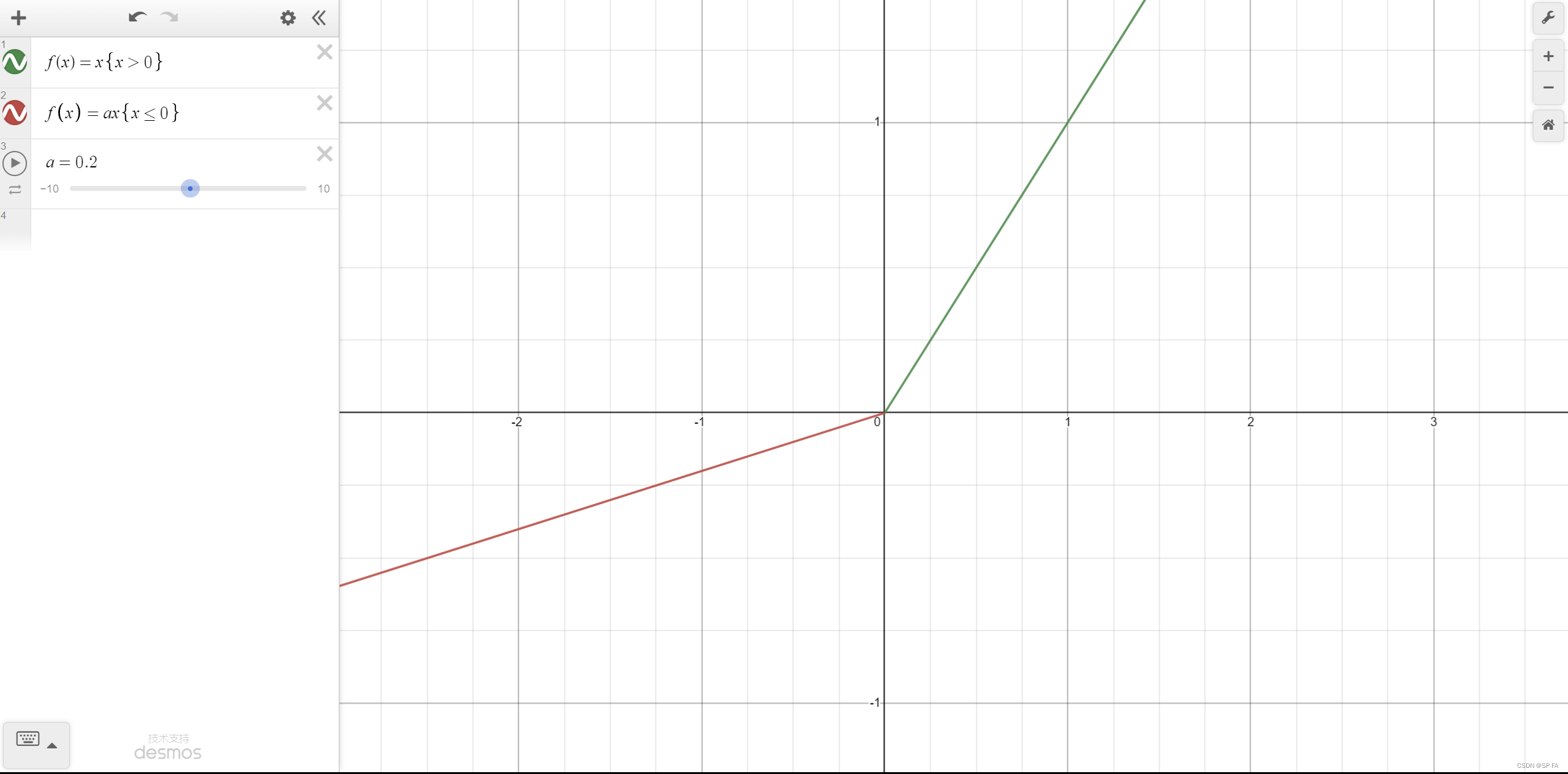
一种专门设计用于解决 Dead ReLU 问题的激活函数
f
(
x
)
=
{
x
x
>
=
0
a
x
x
<
0
f(x)=\begin{cases}x&x>=0\\ax&x<0\end{cases}
f(x)={xaxx>=0x<0其中
a
a
a 值很小,一般在 0.01 左右。
注意: 从理论上来讲,Leaky ReLU 具有 ReLU 的所有优点,且不会有 Dead ReLU 问题,但在实际使用中,没有完全证明 Leaky ReLU 总是比 ReLU 好。
PReLU
和 Leaky ReLU 很像,唯一的不同是函数中的 a a a 是一个可通过反向传播学习的参数。
RReLU
对 Leaky ReLU 的另一种改进。在训练时, a a a 是给定范围内取样的随机变量,而测试时 a a a 变为固定值。这里 a a a 服从均匀分布。
ELU
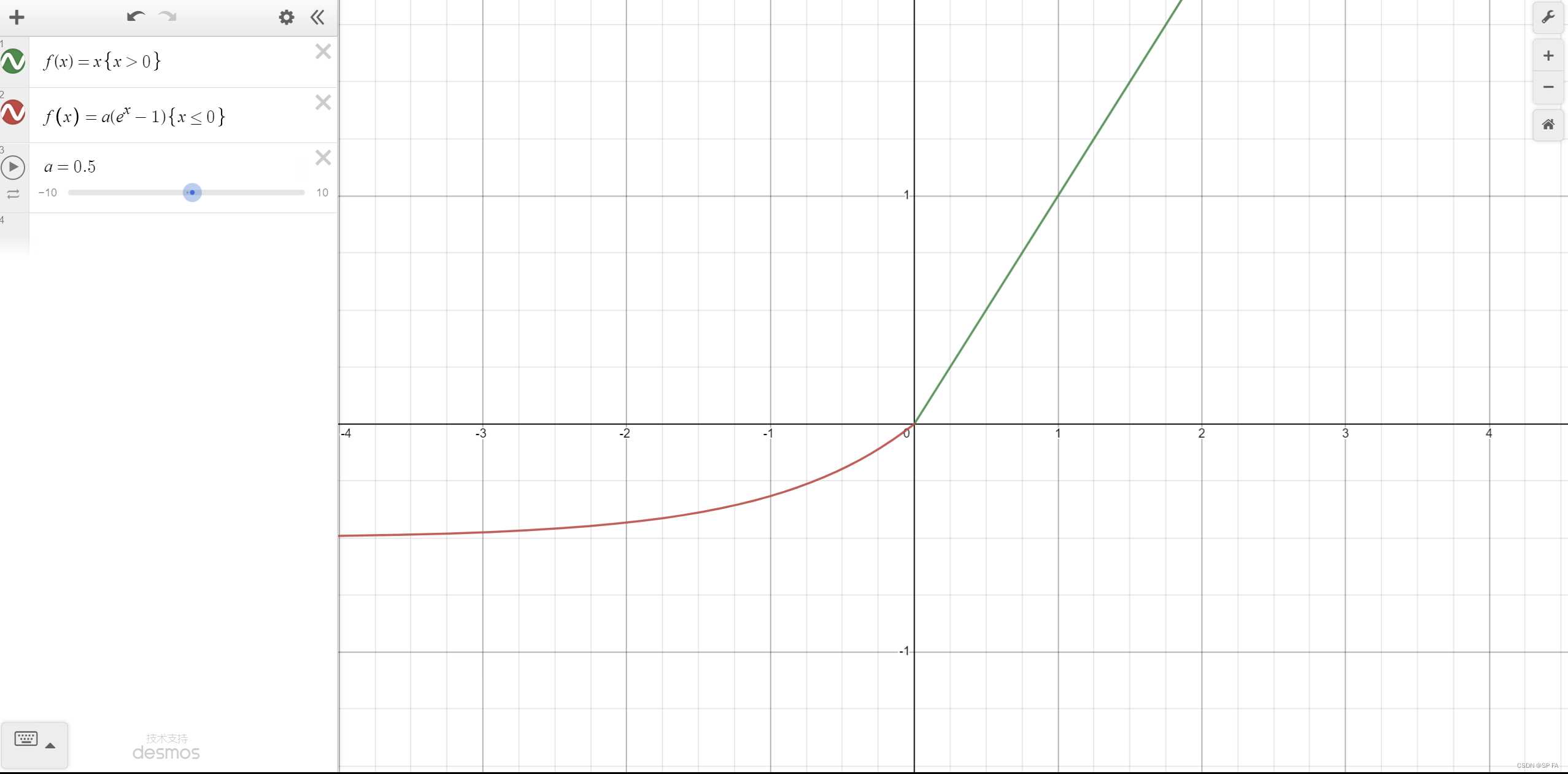
ELU 的提出也解决了 ReLU 的一些问题。 g ( x ) = { x x > = 0 a ( e x − 1 ) x < 0 g(x)=\begin{cases}x&x>=0\\a(e^x-1)&x<0\end{cases} g(x)={xa(ex−1)x>=0x<0优点:
- ReLU 的所有优点
- 没有 Dead ReLU
- 与 ReLU 相比,ELU 有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度。
- 在较小的输入下会饱和至负值,从而减少前向传播的变异和信息。
缺点:
- 有指数运算,计算强度更高
- 从理论上来讲,ELU 具有 ReLU 的所有优点,但在实际使用中,没有完全证明 ELU 总是比 ReLU 好。
SELU
SELU和ELU的形式比较类似,但是多出一个 scale。 g ( x ) = s c a l e ∗ { x x > = 0 a ( e x − 1 ) x < 0 g(x)=scale*\begin{cases}x&x>=0\\a(e^x-1)&x<0\end{cases} g(x)=scale∗{xa(ex−1)x>=0x<0优点:
- 能够对神经网络进行自归一化
CELU
g ( x ) = { x x > = 0 a ( e x a − 1 ) x < 0 g(x)=\begin{cases}x&x>=0\\a(e^\frac xa-1)&x<0\end{cases} g(x)={xa(eax−1)x>=0x<0
GELU
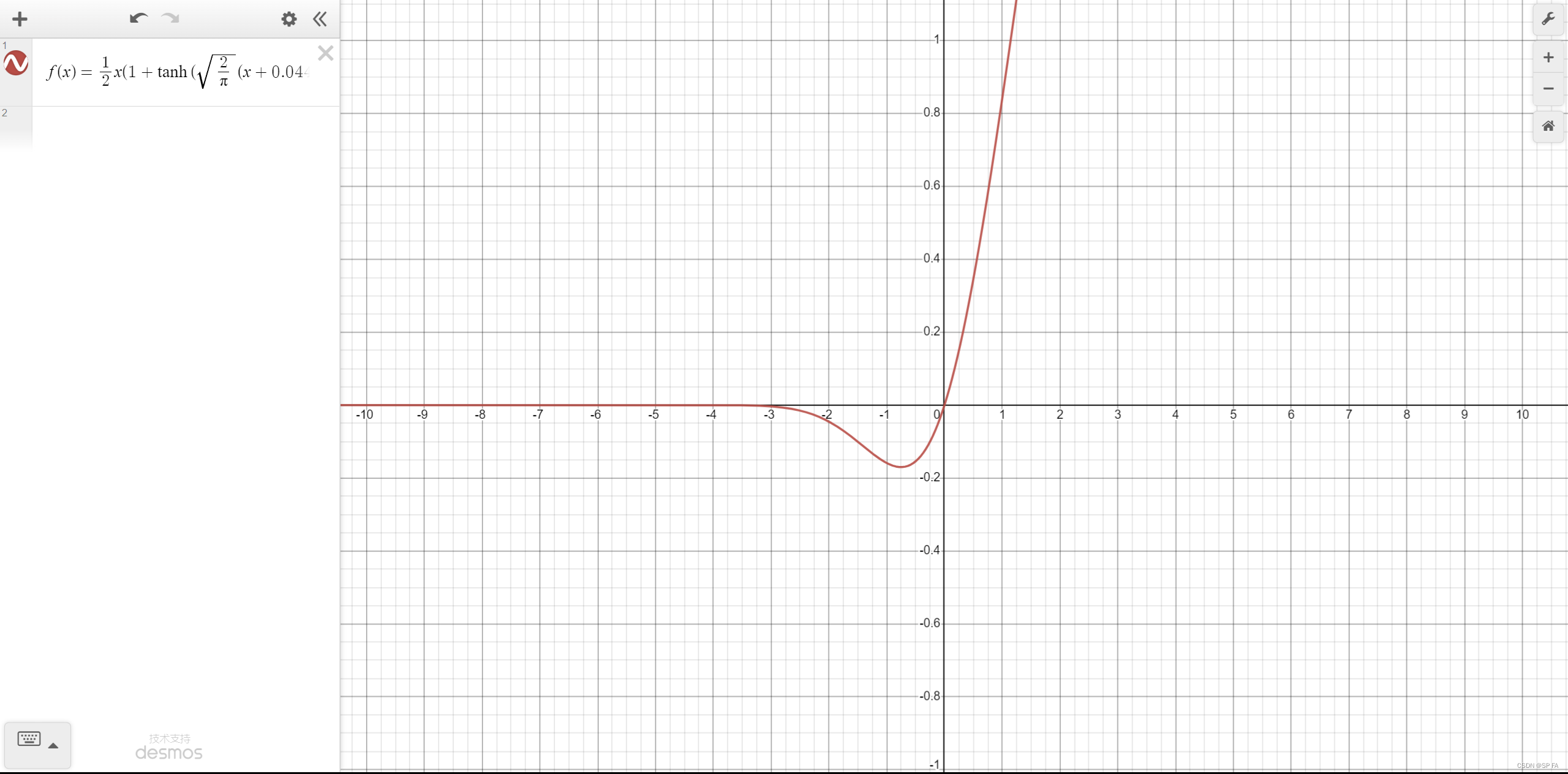
f
(
x
)
=
1
2
x
(
1
+
tanh
(
2
π
(
x
+
0.044715
x
3
)
)
)
f(x)=\frac12x(1+\tanh(\sqrt{\frac2\pi}(x+0.044715x^3)))
f(x)=21x(1+tanh(π2(x+0.044715x3)))GELU 函数结合了 ReLU、Dropout、Zoneout 的思想,并且加入了正态分布的方法。
- ReLU: 输入大于 0 则输出,否则不输出。
- Dropout:随机决定是否输出。
- Zoneout:Dropout 的一个变种,在时间维度上随机决定是否输出,或者可以理解为是否跳过这一步直接到达下一步。
这三者的相同点总结为一句话,就是通过对输入乘上 1 或 0 来控制神经元是否输出。而 GELU 也采用了这个思想,但它是否输出是由自身分布情况决定的,更具体一点,由输入项有多大概率大于其它输入而决定。
更具体一点:
将输入
x
x
x 乘以一个服从伯努利分布的数
m
m
m,而该伯努利分布由依赖于
x
x
x
m
∼
Bernoulli
(
Φ
(
x
)
)
where
Φ
(
x
)
=
P
(
X
≤
x
)
m\sim\text{Bernoulli}(\Phi(x))\\\text{where }\Phi(x)=P(X\le x)
m∼Bernoulli(Φ(x))where Φ(x)=P(X≤x)由于神经元的输入往往遵循正太分布(尤其是深度网络中普遍存在 Batch Normalization 的情况下),所以公式中
X
X
X 表示其它输入,服从标准正态分布
X
∼
N
(
0
,
1
)
X\sim N(0,1)
X∼N(0,1),那么
Φ
(
x
)
\Phi(x)
Φ(x) 就表示标准正态分布的累计分布函数。此时 GELU 函数可以写成:
GELU
(
x
)
=
x
Φ
(
x
)
+
0
∗
x
(
1
−
Φ
(
x
)
)
=
x
Φ
(
x
)
\text{GELU}(x)=x\Phi(x)+0*x(1-\Phi(x))=x\Phi(x)
GELU(x)=xΦ(x)+0∗x(1−Φ(x))=xΦ(x)另外累积分布函数
Φ
(
x
)
\Phi(x)
Φ(x) 可以用误差函数表示:
Φ
(
x
)
=
1
2
[
1
+
erf
(
x
2
)
]
\Phi(x)=\frac12[1+\text{erf}(\frac x{\sqrt2})]
Φ(x)=21[1+erf(2x)] 而误差函数是一个非初等函数,所以我们又需要用一个初等函数 tanh 去拟合,最终就有了上面 GELU 的公式。
优点:
- 似乎是 NLP 领域的当前最佳,尤其在 Transformer 模型中表现最好
- 能避免梯度消失问题
Softmax 函数
用于多分类问题的激活函数,在多类分类问题中,超过两个类标签则需要类成员关系。对于长度为 K K K 的任意实向量,Softmax 可以将其压缩为长度为 K K K,值在 ( 0 , 1 ) (0,1) (0,1) 范围内,并且向量中元素值的总和为 1 的实向量。 S o f t m a x ( z ⃗ ) = e z i ∑ j = 1 K e z j Softmax(\vec z)=\frac{e^{z_i}}{\sum^K_{j=1}e^{z_j}} Softmax(z)=∑j=1KezjeziSoftmax 与正常的 max 函数不同,max 函数仅输出最大值,但 Softmax 会确保较小的值具有较小的概率,并不会直接丢弃。可以认为它是 argmax 函数的概率版本。
缺点:
- 在 0 点不可微
- 负输入的梯度为零,这意味着对于该区域,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
Maxout 函数
f ( x ) = max ( w 1 T x + b 1 , w 2 T x + b 2 , ⋯ , w n T x + b n ) f(x)=\max(w_1^Tx+b_1,w_2^Tx+b_2,\cdots,w_n^Tx+b_n) f(x)=max(w1Tx+b1,w2Tx+b2,⋯,wnTx+bn)可以看出 ReLU 就是它的一个变形。它可以近似任何一个连续函数。只有 2 个 maxout 节点的多层感知机就可以拟合任意的凸函数。单个 Maxout 节点可以解释为对一个实值函数进行分段线性近似 (PWL) ,其中函数上任意两点之间的线段位于凸函数的上方。
但它增加了参数和计算量。
Softplus 函数

f
(
x
)
=
ln
(
1
+
e
x
)
f(x)=\ln(1+e^x)
f(x)=ln(1+ex)类似 ReLU 函数,和 ReLU 一样是单侧抑制,但是相对平滑。
优点:
- 与 ReLU 不同的是,SoftPlus 的导数是连续的、非零的、无处不在的,这一特性可以防止出现 Dead ReLU 现象。
缺点:
- SoftPlus 是不对称的,不以0为中心,存在偏移现象。
- 其导数常常小于1,也可能会出现梯度消失的问题。





![已解决+ CategoryInfo: SecurityError: (:) [ ].ParentContainsErrorRecordException](https://img-blog.csdnimg.cn/aa398ab5583948a0862167c05b0b36b9.png)
![[LeetCode周赛复盘] 第 326 场周赛20230101](https://img-blog.csdnimg.cn/9517bb38599443dcaf74a6a464d68393.png)