【C++ STL】-- 用一棵红黑树的插入实现同时封装map与set

news2024/9/21 14:39:21

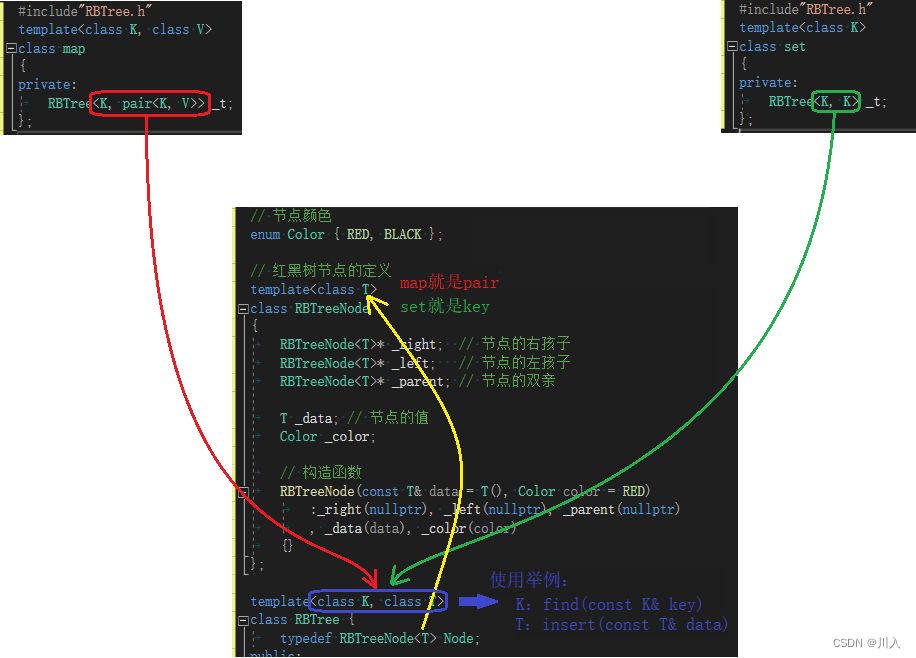
        用一棵红黑树同时封装map与set的意义：所谓的 “用一棵红黑树同时封装map与set” 只是在程序员的角度，通过一系列手段，以一个红黑树同时满足map与set。但是在编译器的角度，实际上并不是一颗树实现的，程序员所写的只是一份模板，map与set是需要各自根据模板实例化的，底层并不是一颗红黑树。（更加轻松实现，更加便于维护）

红黑树的源代码

（红黑树K模型模拟实现)

【C++ STL】-- 红黑树的插入实现_川入的博客-CSDN博客

（未经map与set改进的K模型红黑树的源代码）

#include<iostream>
#include<assert.h>
using namespace std;
// 节点颜色
enum Color{RED, BLACK};
 
// 红黑树节点的定义
template<class ValueType>
struct RBTreeNode {
	RBTreeNode<ValueType>* _right;  // 节点的右孩子
	RBTreeNode<ValueType>* _left;   // 节点的左孩子
	RBTreeNode<ValueType>* _parent; // 节点的双亲
 
	ValueType _data; // 节点的值
	Color _color;
 
	// 构造函数
	RBTreeNode(const ValueType& data = ValueType(), Color color = RED)
		:_right(nullptr), _left(nullptr), _parent(nullptr)
		,_data(data), _color(color)
	{}
};
 
template<class ValueType>
class RBTree {
	typedef RBTreeNode<ValueType> Node;
public:
	bool insert(const ValueType& data)
	{
		// 插入的位置是根节点
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_color = BLACK;
			return true;
		}
 
		Node* parent = nullptr;
		Node* cur = _root;
        // 查找cur插入的位置
		while (cur)
		{
			if (data > cur->_data)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (data < cur->_data)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}
 
		cur = new Node(data);
		cur->_color = RED;
 
		if (cur->_data > parent->_data)
			parent->_right = cur;
		else
			parent->_left = cur;
		cur->_parent = parent;
 
		while (parent && parent->_color == RED)
		{
			Node* grandfather = parent->_parent;
			assert(grandfather);
			assert(grandfather->_color == BLACK);
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				
				//情况一：uncle存在且为红，p、u变黑，g变红。继续向上
				if (uncle && uncle->_color == RED)
				{
					parent->_color = uncle->_color = BLACK;
					grandfather->_color = RED;
					//继续向上
					cur = grandfather;
					parent = cur->_parent;
				}
				else// 情况二+三：uncle不存在 + 存在且为黑
				{
					//情况二：右旋 + p变黑，g变红
					//      g
					//   p     u
					// c
					if (cur == parent->_left)
					{
						RotateR(grandfather);
						parent->_color = BLACK;
						grandfather->_color = RED;
					}
					//情况三：左旋 + 情况二（右旋 + p变黑，g变红）
				    //     g
				    //  p     u
				    //    c
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_color = BLACK;
						grandfather->_color = RED;
					}
					break;
				}
			}
			else
			{
				Node* uncle = grandfather->_left;
 
				//情况一：uncle存在且为红，p、u变黑，g变红。继续向上
				if (uncle && uncle->_color == RED)
				{
					parent->_color = uncle->_color = BLACK;
					grandfather->_color = RED;
					//继续向上
					cur = grandfather;
					parent = cur->_parent;
				}
				else// 情况二+三：uncle不存在 + 存在且为黑
				{
					//情况二：左旋 + p变黑，g变红
					//      g
					//   u     p
					//           c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_color = BLACK;
						grandfather->_color = RED;
					}
					//情况三：右旋 + 情况二（左旋 + p变黑，g变红）
					//      g
					//   u     p
					//       c
					else
					{
						RotateR(parent);
						RotateL(grandfather);
						cur->_color = BLACK;
						grandfather->_color = RED;
					}
					break;
				}
			}
		}
		_root->_color = BLACK;
		return true;
	}
 
	// 利用递归前序按升序打印红黑树
	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}
 
	// 检测是否符合红黑树
	bool IsBalance()
	{
		if (_root == nullptr)
		{
			return true;
		}
 
		// 判断根节点是否为黑色
		if (_root->_color == RED)
		{
			cout << "根节点不黑色" << endl;
			return false;
		}
 
		int benchMark = 0; //某路径的黑节点个数，作为基准值
		return PrevCheck(_root, 0, benchMark);
	}
 
private:
	// 利用深度优先
	bool PrevCheck(Node* root, int blackNum, int& benchMark) //利用引用保存基准值
	{
		if (root == nullptr)
		{
			if (benchMark == 0) //将第一个路径的黑节点个数给benchMark，作为基准值
				benchMark = blackNum;
			else if(blackNum != benchMark)
				return false;
			return true;
		}
 
		if (root->_color == BLACK)
			++blackNum;
 
		// 检查是否有连续的红色节点
		if (root->_color == RED && root->_parent->_color == RED)
		{
			cout << "存在连续的红节点" << endl;
				return false;
		}
 
		return PrevCheck(root->_left, blackNum, benchMark)
			&& PrevCheck(root->_right, blackNum, benchMark);
	}
 
	// 前序递归
	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;
 
		_InOrder(root->_left);
		cout << root->_data << " ";
		_InOrder(root->_right);
	}
 
	// 右单旋
	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
 
		// 将subL连接到parent的左
		parent->_left = subLR;
		if (subLR) // 可能subL的右子树不存在
			subLR->_parent = parent;
 
		Node* pparent = parent->_parent;
 
		// 将parent连接到subL的右节点上，成为subL的右子树
		subL->_right = parent;
		parent->_parent = subL;
 
		// 将parent的父节点状态给予subL
		if (_root == parent) // parent是根
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else // parent不是根
		{
			if (pparent->_left == parent)
				pparent->_left = subL;
			else
				pparent->_right = subL;
			subL->_parent = pparent;
		}
	}
 
	// 左单旋
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
 
		// 将subR连接到parent的右
		parent->_right = subRL;
		if (subRL) // 可能subR的左子树不存在
			subRL->_parent = parent;
 
		Node* pparent = parent->_parent;
 
		// 将parent连接到subR的左节点上，成为subR的左子树
		subR->_left = parent;
		parent->_parent = subR;
 
		// 将parent的父节点状态给予subR
		if (_root == parent) // parent是根
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else // parent不是根
		{
			if (pparent->_left == parent)
				pparent->_left = subR;
			else
				pparent->_right = subR;
			subR->_parent = pparent;
		}
	}
 
	Node* _root = nullptr;
};
 
void TestRBTree()
{
	size_t N = 100;
	srand(time(0));
	RBTree<int> t;
	for (size_t i = 0; i < N; ++i)
	{
		int x = rand();
		t.insert(x);
	}
 
	t.InOrder();
 
	if (t.IsBalance())
		cout << "是红黑树" << endl;
	else
		cout << "不是红黑树" << endl;
}
 
int main()
{
	TestRBTree();
	return 0;
}

模板参数的改进

        我们知道set是经典的k模型，map是经典的kv模型。那么是不是代表，对于set与map的实现需要分别利用k模型的红黑树和kv模型的红黑树，需要两颗红黑树？

        但是STL其实是非常注意复用性的（如：迭代器的复用 - 普通迭代器与const迭代器、栈队列复用之前的容器、优先级队列复用之前的容器） ，并不会让两份代码，大结构和逻辑几乎都是类似的，只有细节的些许差距，以此写两份，导致代码冗余。

让我们看看源代码对齐的处理：

我们简单的实现一下：

模板参数的再次改进

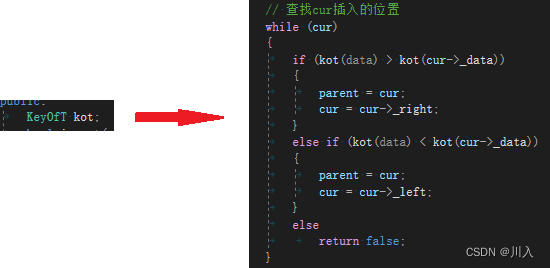
        在原来的基础上：对于插入点的查找，插入点的插入都是需要利用data数据与比较路径上节点的_data成员的比较：

  • 对于set是没有问题的，set 以RBTree<K, K> _t，将key传给了模板参数T，所以data是key类型的，对于比较是没有问题的。
  • 对于map是有问题的，map 以PBTree<K, pair<K, V>>，将pair<K, V>传给了模板参数T，所以data是pair<K, V>类型的：而pair对于比较的operator重载是：

pair比较重载的相关文档

以 operator> 举例：

        其是 “data1.frist > data2.frist” 或者 “data1.frist < data2.frist 的情况下 data1.second > data2..second” 都是属于data1 > data2。 所以pair的比较重载是不可用的，而由于pair已经提供了比较重载，我们也就没法自己写比较重载。

        基于此基础上，我们就需要增加一个模板参数，一个仿函数。

map与set：

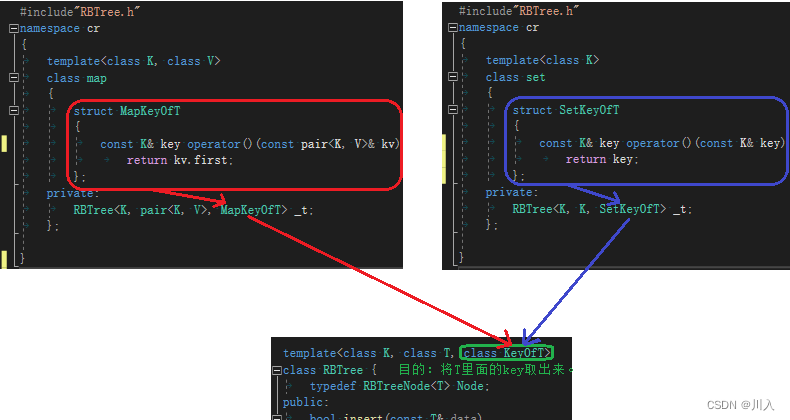
        即：根据仿函数比较的地方我们也需要进行改进（如：insert的插入位置查找）：

正向迭代器

        红黑树的正向迭代器，实际上是对结点指针进行了封装，模板化了T，T&，T*，分别用于结点指针，*与->的operator的重载函数的返回值。

template<class T, class Ref, class Ptr>
struct __RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __RBTreeIterator<T, Ref, Ptr> Self;
	Node* _node; //对节点指针进行封装

    //构造函数
	__RBTreeIterator(Node* node)
		:_node(node)
	{}

    // ……
}

template<class K, class T, class KeyOfT>
class RBTree {
public://typedef会受访问限定符干扰	
    typedef __RBTreeIterator<T, T&, T*> iterator;
    // ……
}

当正向迭代器调用*是，重载operator*返回对应数据的引用即可：

Ref operator*() //Pef：T&
{
	return _node->_data;
}

当正向迭代器调用->是，重载operator->返回对应数据的地址即可：

Ptr operator->()
{
	return &_node->_data;
}

对于==与!=的运算符重载，只需要判断正向迭代器中封装的，对应节点地址是否相等即可：

bool operator!=(const Self& s)const
{
	return _node != s._node;
}

bool operator==(const Self& s)const
{
	return _node == s._node;
}

        对于正向迭代器的++与--运算符的重载函数，最佳的实现的方式是非递归，而由于此时三叉链的节点（即，同时有：parent，left, right的指针）无需利用栈就可以更加直接的实现：

operator前置++

逻辑如下：

    因为，遍历红黑树的核心是：左子树 根 右子树

  • 右子树不为空，++就是找右子树的中序第一个节点（最左节点）：

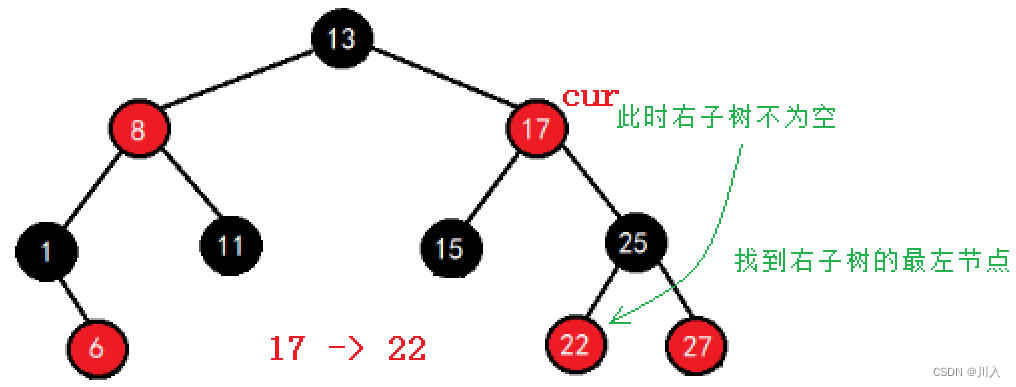
  • 右子树为空，++就是找孩子不是父亲右的那个祖先父亲节点：

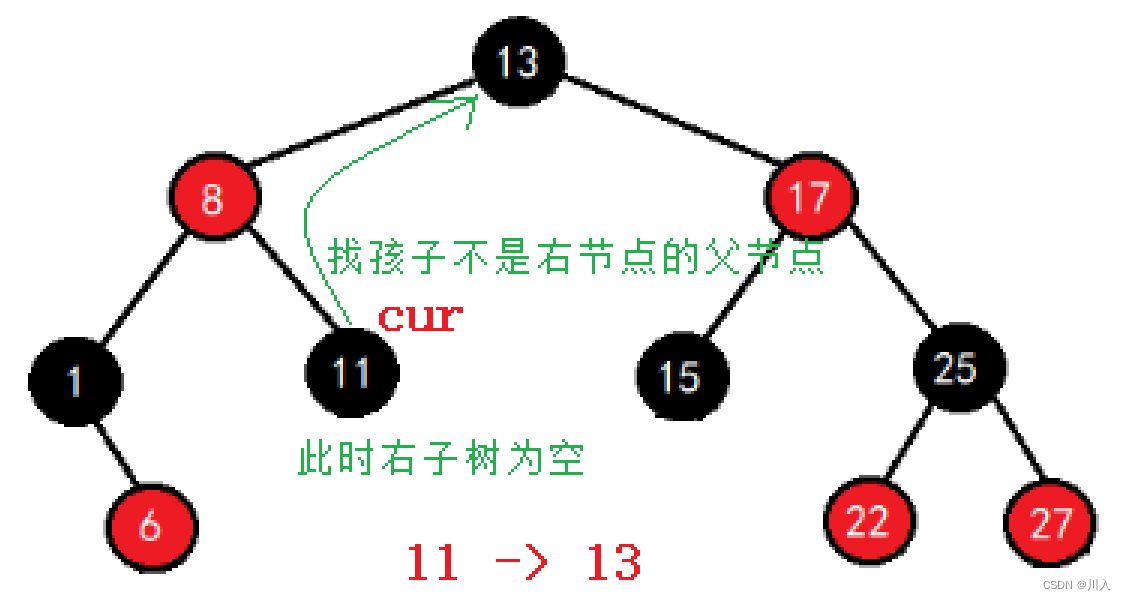
         同时实现了，正向迭代器的结尾是end()时为：nullptr。

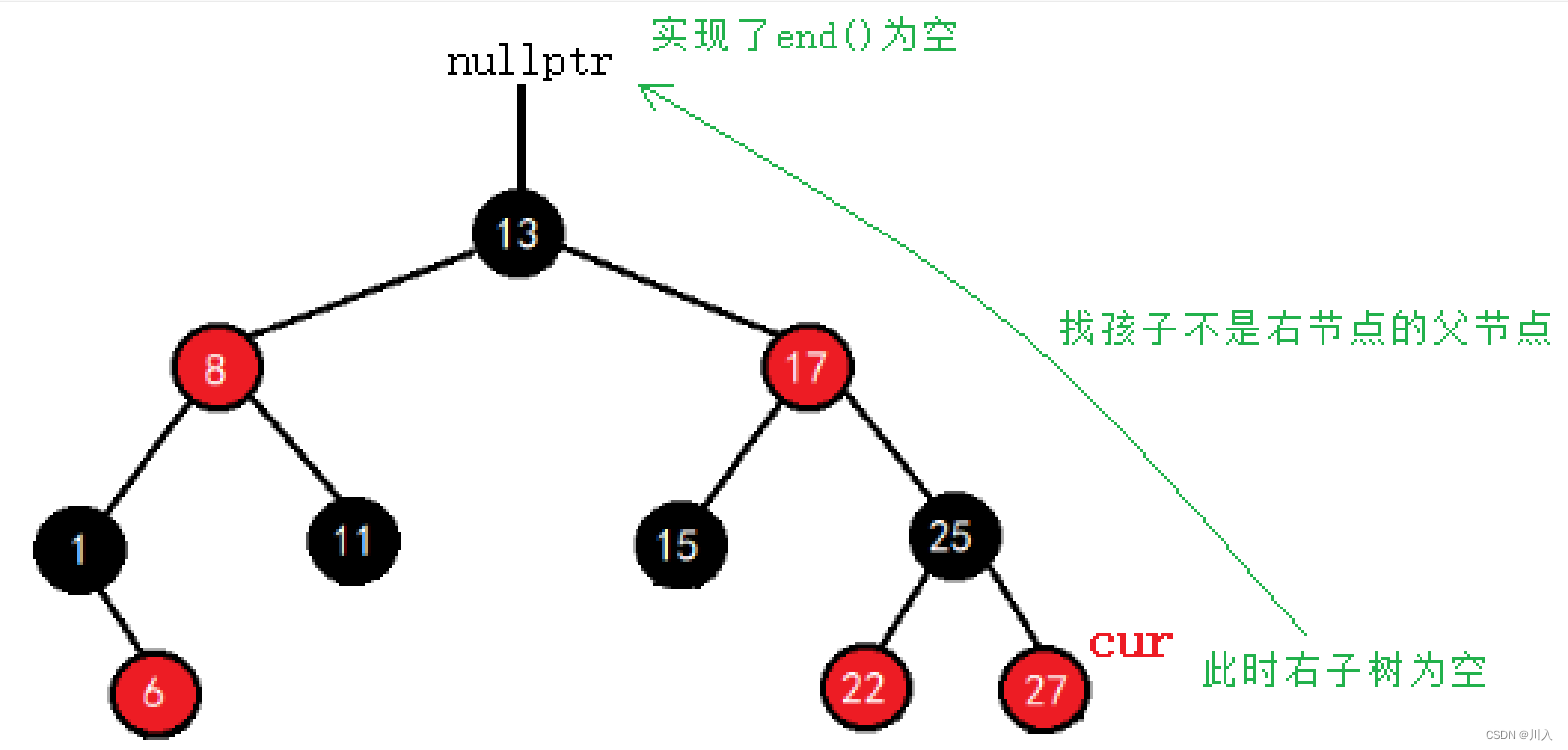
Self& operator++()
{
	// 下一个就是：右子树的最左节点
	if (_node->_right)
	{
		Node* left = _node->_right;
		while (left->_left)
			left = left->_left;
		_node = left;
	}
	else
	{
		// 下一个就是：找孩子不是父亲右的那个祖先父亲节点
		Node* root = _node;
		Node* parent = _node->_parent;
		while (parent && root == parent->_right)
		{
			root = root->_parent;
			parent = root->_parent;
		}
		_node = parent;
	}
	return *this;
}

operator前置--

    因为，到过来遍历红黑树的核心是：右子树 根 左子树，所以与前置++的实现原理一样：

  • 左子树不为空，- - 就是找左子树的中序最后一个节点（最右节点）
  • 左子树为空，- - 就是找孩子不是父亲左的那个祖先父亲节点
Self& operator--()
{
	// 上一个就是：左子树的最右节点
	if (_node->_left)
	{
		Node* right = _node->_left;
		while (right->_right)
		{
			right = right->_right;
		}
		_node = right;
	}
	else
	{
		// 上一个就是：找孩子不是父亲左的那个祖先父亲节点
		Node* root = _node; v
			Node* parent = root->_parent;
		while (parent && root == parent->_left)
		{
			root = root->_parent;
			parent = root->_parent;
		}
		_node = parent;
	}
	return *this;
}

insert

        由于我们需要实现operator[]，所以insert的返回值需要是pair<iterator, bool>，如果没有就插入，如果已经有返回那个已经在的节点的迭代器：

map.h

pair<iterator, bool>  insert(const pair<K, V>& kv)
{
	return _t.insert(kv);
}

set.h

pair<iterator, bool> insert(const K& key)
{
	return _t.insert(key);
}

RBTree.h

pair<iterator, bool> insert(const T& data)
{
	KeyOfT kot;

	// 插入的位置是根节点
	if (_root == nullptr)
	{
		_root = new Node(data);
		_root->_color = BLACK;
		return make_pair(iterator(_root), true);
	}

	Node* parent = nullptr;
	Node* cur = _root;
	// 查找cur插入的位置
	while (cur)
	{
		if (kot(data) > kot(cur->_data))
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (kot(data) < kot(cur->_data))
		{
			parent = cur;
			cur = cur->_left;
		}
		else
			return make_pair(iterator(cur), false);
	}

	cur = new Node(data);
	Node* newnode = cur; //用于返回iterator封装新增节点的地址
	cur->_color = RED;

	if (kot(cur->_data) > kot(parent->_data))
		parent->_right = cur;
	else
		parent->_left = cur;
	cur->_parent = parent;

	while (parent && parent->_color == RED)
	{
		Node* grandfather = parent->_parent;
		assert(grandfather);
		assert(grandfather->_color == BLACK);
		if (grandfather->_left == parent)
		{
			Node* uncle = grandfather->_right;

			//情况一：uncle存在且为红，p、u变黑，g变红。继续向上
			if (uncle && uncle->_color == RED)
			{
				parent->_color = uncle->_color = BLACK;
				grandfather->_color = RED;
				//继续向上
				cur = grandfather;
				parent = cur->_parent;
			}
			else// 情况二+三：uncle不存在 + 存在且为黑
			{
				//情况二：右旋 + p变黑，g变红
				//      g
				//   p     u
				// c
				if (cur == parent->_left)
				{
					RotateR(grandfather);
					parent->_color = BLACK;
					grandfather->_color = RED;
				}
				//情况三：左旋 + 情况二（右旋 + p变黑，g变红）
				//     g
				//  p     u
				//    c
				else
				{
					RotateL(parent);
					RotateR(grandfather);
					cur->_color = BLACK;
					grandfather->_color = RED;
				}
				break;
			}
		}
		else
		{
			Node* uncle = grandfather->_left;

			//情况一：uncle存在且为红，p、u变黑，g变红。继续向上
			if (uncle && uncle->_color == RED)
			{
				parent->_color = uncle->_color = BLACK;
				grandfather->_color = RED;
				//继续向上
				cur = grandfather;
				parent = cur->_parent;
			}
			else// 情况二+三：uncle不存在 + 存在且为黑
			{
				//情况二：左旋 + p变黑，g变红
				//      g
				//   u     p
				//           c
				if (cur == parent->_right)
				{
					RotateL(grandfather);
					parent->_color = BLACK;
					grandfather->_color = RED;
				}
				//情况三：右旋 + 情况二（左旋 + p变黑，g变红）
				//      g
				//   u     p
				//       c
				else
				{
					RotateR(parent);
					RotateL(grandfather);
					cur->_color = BLACK;
					grandfather->_color = RED;
				}
				break;
			}
		}
	}
	_root->_color = BLACK;
	return make_pair(iterator(newnode), true);
}

map的operator[]

        operator[]就不是在红黑树那层套了，因为只有kv才有方括号，即set没有方括号。红黑树又没有办法确定是k模型，还是kv模型。即map自己套就行了。

V& operator[](const K& key)
{
	pair<iterator, bool> ret = insert(make_pair(key, V())); // V()：int就是0、指针就是nullptr、自定义就是默认构造的值
	// 有即返回有的
	// 没有即返回刚插入的
	return ret.first->second;
	//ret->first == pair<iterator, bool>里面第一个元素，迭代器
}

        本质上map与set可以说是什么都没有写，都是下层的封装。map与set空有其表，靠底层的红黑树。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/133088.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

机器学习 10：激活函数大全

机器学习 10：激活函数大全

虽称为激活函数大全&#xff0c;但也不敢太过自满&#xff0c;如有遗漏与错误&#xff0c;还请指正 文章目录线性激活函数Sigmoid 函数LogSigmoidSwishTanh / 双曲正切激活函数TanhShrinkSoftsignReLU 函数BReLULeaky ReLUPReLURReLUELUSELUCELUGELUSoftmax 函数Maxout 函数Sof…
阅读更多...
Android 实现多语言

Android 实现多语言

工具下载连接 链接&#xff1a;https://pan.baidu.com/s/1Wq9DTzhP2fkHXLEbOQFr9A?pwdlmcz 提取码&#xff1a;lmcz 1.将你需要的翻译的strings放到exe目录下 2.双击执行xml转xls.exe 英文 日文 韩文&#xff08;使用空格分割&#xff09;回车&#xff0c;会在当前目录下生…
阅读更多...
jvm学习的开端（一）----类的加载（类加载子系统）

jvm学习的开端（一）----类的加载（类加载子系统）

文章目录1.Loading&#xff08;加载阶段&#xff09;2.Linking&#xff08;链接阶段&#xff09;2.lnitialization&#xff08;初始化阶段&#xff09;来自 百度百科&#xff1a; 类加载器子系统负责从文件系统或者网络中加载class文件&#xff0c;class文件在文件开头有特定的…
阅读更多...
【java项目】飞机大战

【java项目】飞机大战

文章目录项目-飞机大战窗口的创建背景图片的添加/点击事件的启动游戏物体父类的编写背景的移动双缓存技术--解决文字闪动背景图片循环出现我方战斗机的添加和鼠标控制添加首颗子弹批量添加子弹敌方飞机的批量添加功能我方子弹与敌方飞机的碰撞检测我方子弹与敌方飞机碰撞时的处…
阅读更多...
单片机基础之单片机中断、定时器中断、PWM及SG90舵机的初识认知

单片机基础之单片机中断、定时器中断、PWM及SG90舵机的初识认知

目录 一、初探单片机中断 二、定时器中断相关寄存器 1、中断寄存器 2、中断结构 3、用定时器中断方式控制LED&#xff0c;代码编程测试 三、初识PWM 1、什么是占空比 2、如何输出PWM信号 四、SG90舵机基本认知 1、什么是舵机 2、怎么控制舵机 3、舵机编程实战 一、…
阅读更多...
Jetson nano 入手系列之2—板载摄像头IMX219启动

Jetson nano 入手系列之2—板载摄像头IMX219启动

Jetson nano 入手系列之2—板载摄像头IMX219启动1.亚克力板安装2.摄像头启动3.nvgstcapture常用命令3.1 Set sensor orientation3.2 Get Image Capture Resolution3.3 Capture3.4 quit参考文献Jetson nano 入手系列&#xff1a; Jetson nano 入手系列之1—如何SSH远程登录 Jets…
阅读更多...
Redis学习(一)

Redis学习(一)

Redis入门 Redis是一个基于内存的key-value结构数据库&#xff0c;读写性能较高 Redis数据类型 Redis存储的是key-value结构的数据&#xff0c;其中key是字符串类型&#xff0c;value有5种数据类型&#xff1a; 1.字符串 string 2.哈希 hash 3.列表 list 4.集合 set 5.有序集…
阅读更多...
Altium Designer 20 凡亿教育视频学习-01

Altium Designer 20 凡亿教育视频学习-01

课程视频&#xff1a;第1课 课程介绍.mp4_哔哩哔哩_bilibili 第一部分学习 学习方法 工程具备文件 一定需要先建立工程&#xff0c;再来创建原理图库、原理图等文件 栅格大小改变 栅格的大小我们常在绘制原理图的时候改变&#xff0c;因为有时候我们需要画一个细线&#…
阅读更多...
【PCB专题】什么是通孔、盲孔、埋孔？

【PCB专题】什么是通孔、盲孔、埋孔？

PCB板是由基板和PP叠加而成的。不同层上走了各种信号线和电源，这些信号和电源在不同的电路层之间切换时需要依靠过孔（通孔、盲孔和埋孔）连接。如下图所示的6层板，使用了2阶HDI方案：有机械孔和激光孔。 过孔的作用就像是水管一样，连接了不同的平面。PCB板上的过孔作用就是…
阅读更多...
函数的定义和调用 与 this指向

函数的定义和调用 与 this指向

1、函数的定义和调用 1.1、函数的定义方式 函数声明方式 function 关键字 (命名函数)函数表达式 (匿名函数)new Function() var fn new Function(参数1,参数2..., 函数体)&#xff08;1&#xff09;Function 里面参数都必须是字符串格式 &#xff08;2&#xff09;第三种方式…
阅读更多...
已解决+ CategoryInfo: SecurityError: （:） [ ].ParentContainsErrorRecordException

已解决+ CategoryInfo: SecurityError: （:） [ ].ParentContainsErrorRecordException

已解决无法加载文件 E:\day_01\Scripts\activate.ps1&#xff0c;因为在此系统上禁止运行脚本。有关详细信息&#xff0c;请参阅 https:/go.microsoft.com/fwlink/?LinkID135170 中的about_Execution_Policies。 CategoryInfo: SecurityError: &#xff08;:&#xff09; [ ]…
阅读更多...
[LeetCode周赛复盘] 第 326 场周赛20230101

[LeetCode周赛复盘] 第 326 场周赛20230101

[LeetCode周赛复盘] 第 326 场周赛20230101 一、本周周赛总结二、 [Easy] 6278. 统计能整除数字的位数1. 题目描述2. 思路分析3. 代码实现三、[Medium] 6279. 数组乘积中的不同质因数数目1. 题目描述2. 思路分析3. 代码实现四、[Medium] 6196. 将字符串分割成值不超过 K 的子字…
阅读更多...
路由 NAT（简介、静态NAT、动态NAT、NATServer、NAPT、Easy-ip、NAT地址映射表）

路由 NAT（简介、静态NAT、动态NAT、NATServer、NAPT、Easy-ip、NAT地址映射表）

4.1.0 路由 NAT&#xff08;简介、静态NAT、动态NAT、NATServer、NAPT、Easy-ip、NAT地址映射表&#xff09; 目录简介NAT地址映射表静态NAT简介操作案例动态NAT简介操作案例NAT Server简介操作案例NAPT简介操作案例Easy-ip简介操作案例简介 为了有效节约公网IPv4地址&#xf…
阅读更多...
QT 学习笔记（十二）

QT 学习笔记（十二）

文章目录一、文件系统1. 文件系统简介2. 文件系统分类二、基本文件操作1. QFile 读文件2. QFile 写文件3. QFileInfo 获取文件信息三、基本文件操作代码1. 主窗口头文件 widget.h2. 主窗口源文件 widget.cpp由于每次代码都是在原有程序上修改&#xff0c;因此除了新建项目&…
阅读更多...
物联网与射频识别技术，课程实验（三）

物联网与射频识别技术，课程实验（三）

实验3—— 时隙ALOHA(S-ALOHA)算法的实现及其性能分析 实验说明&#xff1a; 1. 利用Python或Matlab模拟时隙ALOHA算法&#xff1b; 分析标签数量k、时隙大小t对信道利用率的影响&#xff0c;其中&#xff0c; 信道利用率发送数据的时间/(发送数据的时间信道空闲的时间) 3. …
阅读更多...
10、中断系统概述

10、中断系统概述

目录 0x01、异常类型 0x0001、系统异常清单 0x0002、外部中断清单 0x02、NVIC 简介 0x0001、NVIC 寄存器 0x0002、NVIC 中断配置固件库 0x03、优先级 0x0001、优先级定义 0x0002、优先级分组 0x0003、中断编程 0x01、异常类型 STM32F103 在内核水平上搭载了一个异常响…
阅读更多...
重金打造SEA浩瀚架构，吉利的野心绝不仅仅是一个平台

重金打造SEA浩瀚架构，吉利的野心绝不仅仅是一个平台

&#xff08;作者&#xff1a;贝贝。常年供职于某外资整车企业产品规划部门&#xff0c;负责全球车型在国内的引入和投放&#xff09;最近几个月&#xff0c;吉利旗下的中高端电动车品牌极氪汽车销量一路走高。单凭借极氪001一款车型&#xff0c;10月、11月交付量连续破万&…
阅读更多...
查找：折半查找、平衡二叉树、散列表（习题-1、5、6）二叉排序树（习题-2、3、4）

查找：折半查找、平衡二叉树、散列表（习题-1、5、6）二叉排序树（习题-2、3、4）

一个不知名大学生&#xff0c;江湖人称菜狗 original author: jacky Li Email : 3435673055qq.com Time of completion&#xff1a;2023.1.1 Last edited: 2023.1.1 目录 查找&#xff1a;折半查找、平衡二叉树、散列表&#xff08;习题-1、5、6&#xff09; 第1关&#xff1…
阅读更多...
04.spring源码循环依赖终极讲解

04.spring源码循环依赖终极讲解

1.Spring怎么解决循环依赖 我们都知道&#xff0c;单例Bean初始化完成&#xff0c;要经历三步&#xff1a; 注入就发生在第二步&#xff0c;属性赋值&#xff0c;结合这个过程&#xff0c;Spring 通过三级缓存解决了循环依赖&#xff1a; 一级缓存 : Map<String,Object>…
阅读更多...
PUCCH传输UCI信息

PUCCH传输UCI信息

上报HARQ-ACK 时序 传输HARQ-ACK信息的时序不再像4G那样固定&#xff0c;而是由基站侧配置给UE。有下面几种情况&#xff1a; 如果UE收到的是DCI format 1_0&#xff0c;其中的字段’PDSCH-to-HARQ_feedback timing indicatior’指示HARQ-ACK与PDSCH的时序关系&#xff0c;该…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023