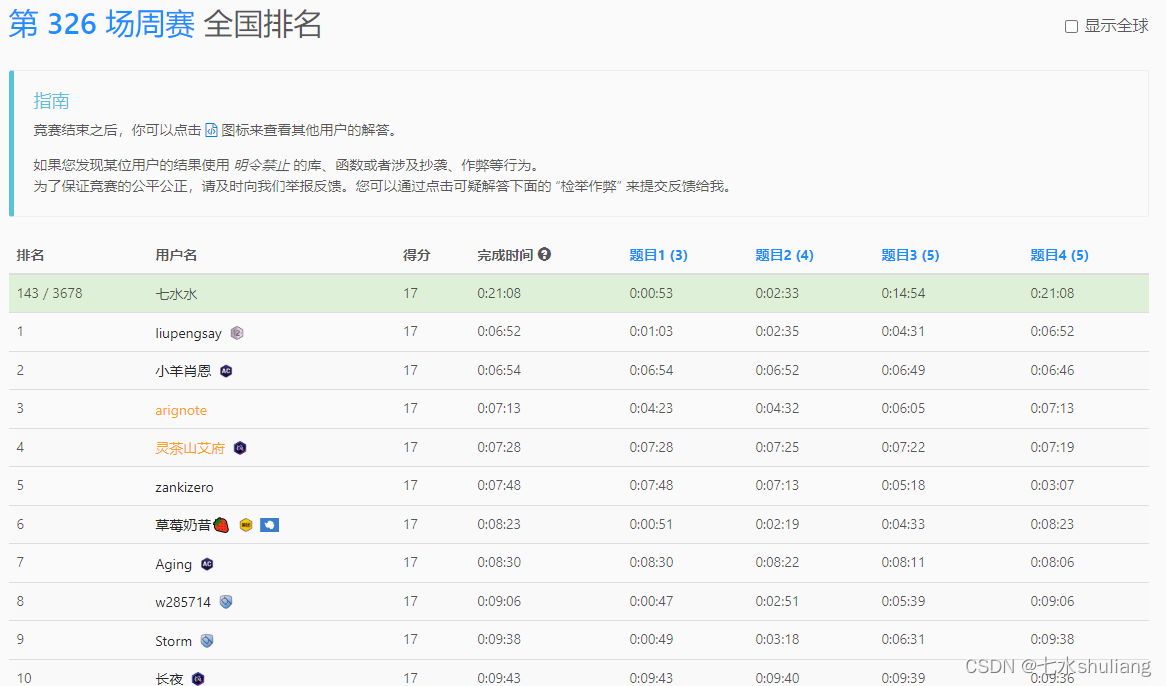
一、本周周赛总结

• 新年福利局。
• T1 模拟。
• T2 分解质因数模板。
• T3 DP。
• T4 埃氏筛模板。
  

二、 [Easy] 6278. 统计能整除数字的位数

链接: 6278. 统计能整除数字的位数

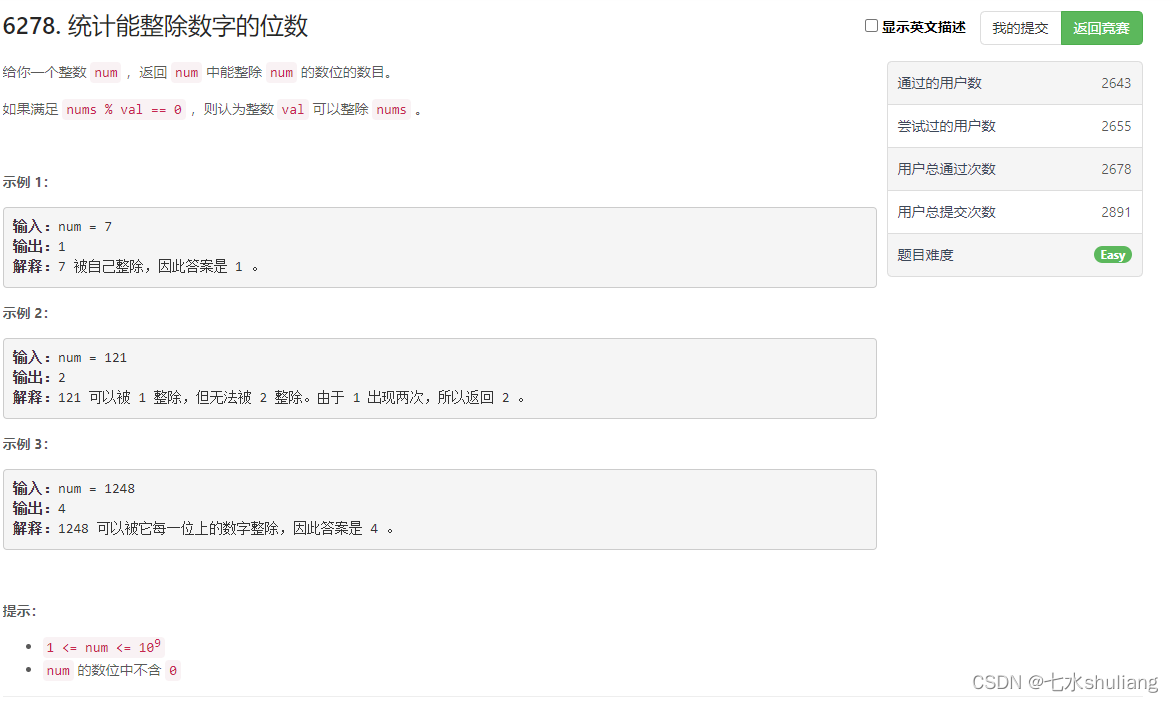
1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def countDigits(self, num: int) -> int: 
        s = str(num)
        ans = 0
        for c in s:
            if num % int(c) ==0:
                ans +=1
        return ans 

三、[Medium] 6279. 数组乘积中的不同质因数数目

链接: 6279. 数组乘积中的不同质因数数目

1. 题目描述

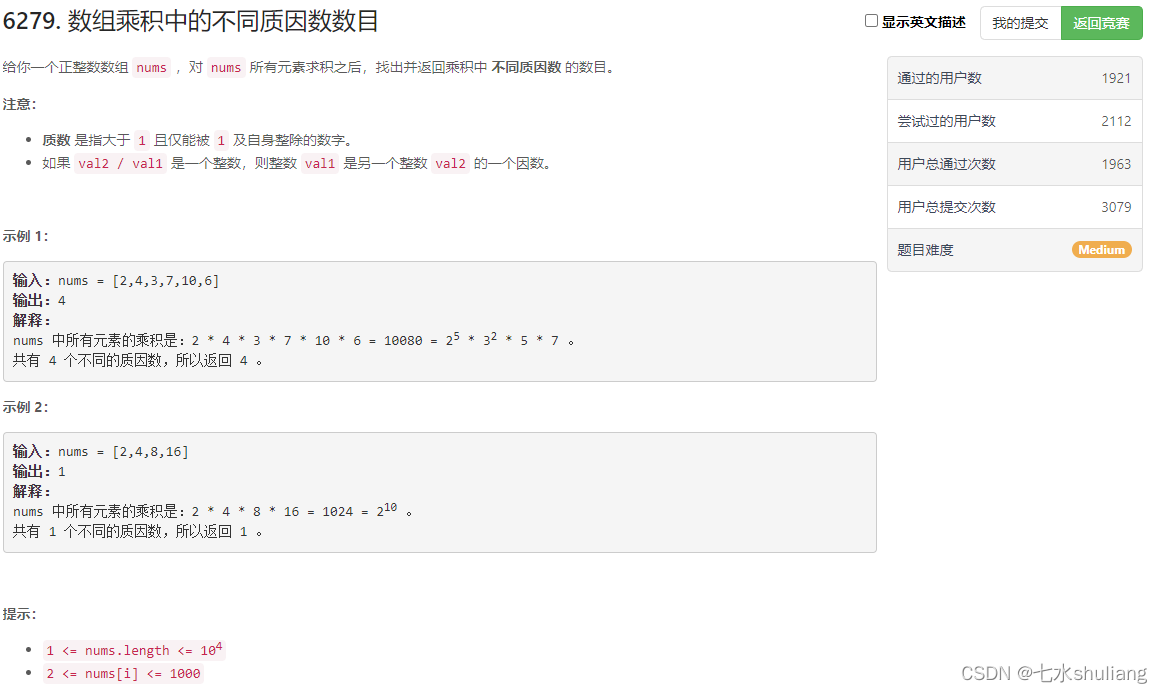
2. 思路分析

贴模板。

• 都乘到一起找质因数就是分别找质因数然后去重，因此用set记录并集即可。

3. 代码实现

def get_prime_reasons(x):
    # 获取x的所有质因数，虽然是两层循环且没有判断合数，但复杂度依然是O(sqrt(x))
    # 由于i是从2开始增加，每次都除完，因此所有合数的因数会提前除完，合数不会被x整除的
    if x == 1:
        return Counter()
    ans = Counter()
    i = 2
    while i*i<=x:
        while x%i==0:
            ans[i] += 1
            x //= i 
        i += 1
    if x > 1: ans[x] += 1
    return ans

class Solution:
    def distinctPrimeFactors(self, nums: List[int]) -> int:
        ans = set()
        for x in nums:
            p = get_prime_reasons(x)
            ans |= set(p.keys())
        return len(ans)

四、[Medium] 6196. 将字符串分割成值不超过 K 的子字符串

链接: 6196. 将字符串分割成值不超过 K 的子字符串

1. 题目描述

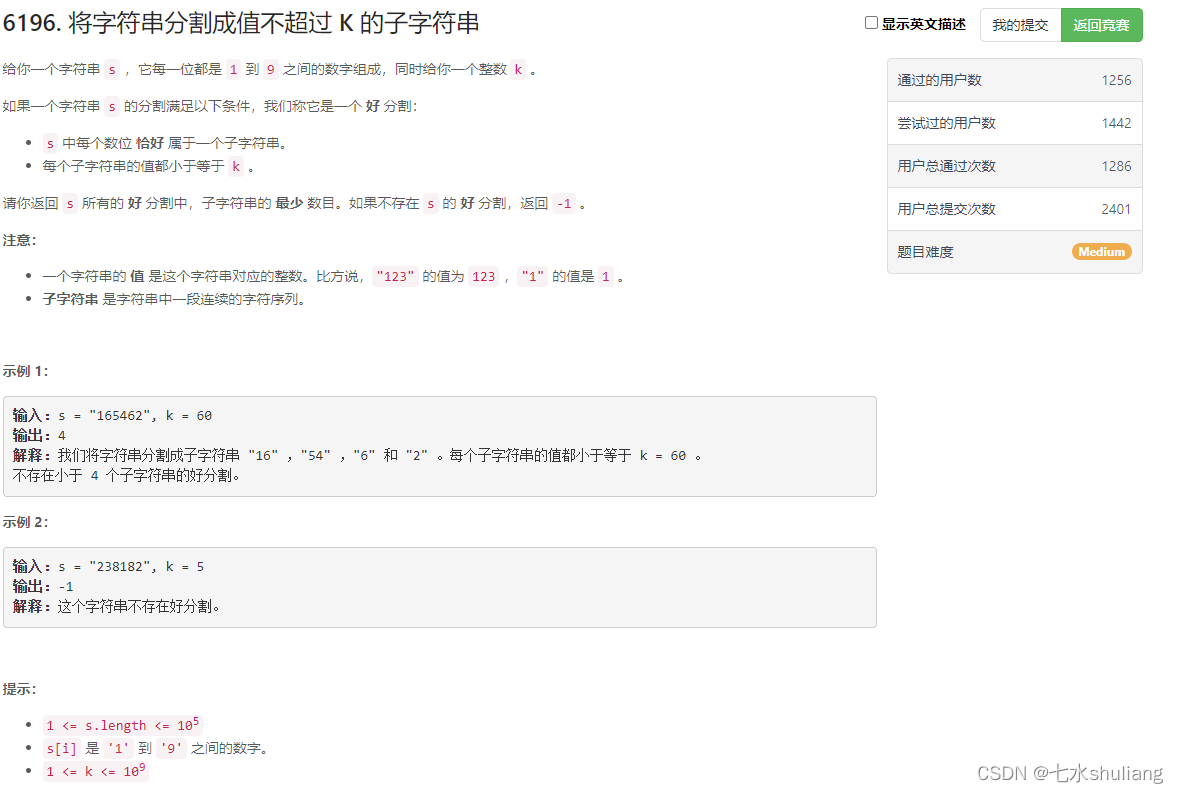
2. 思路分析

• dp。
• 定义f[i]为前i个数能做到的最小分割。
• 转移，f[i] = max{f[l-1]+1}, 其中s[l+1:i+1]<=k
• 显然从i向前找l即可，由于k<=1e9，则最多找10位，总复杂度不会超过1e6。
• 实现时，f向右偏移一位方便编码。

3. 代码实现

class Solution:
    def minimumPartition(self, s: str, k: int) -> int:
        if k<10 and any(int(x)>k for x in s):
            return -1
        n = len(s)
        m = len(str(k))
        f = [0]+[inf]*n
        for i in range(n):
            for j in range(m):
                l = max(0,i-j)
                if int(s[l:i+1]) <= k:
                    f[i+1] = min(f[i+1], f[l]+1)
        return f[-1]

五、[Hard] 6280. 范围内最接近的两个质数

链接: 6280. 范围内最接近的两个质数

1. 题目描述

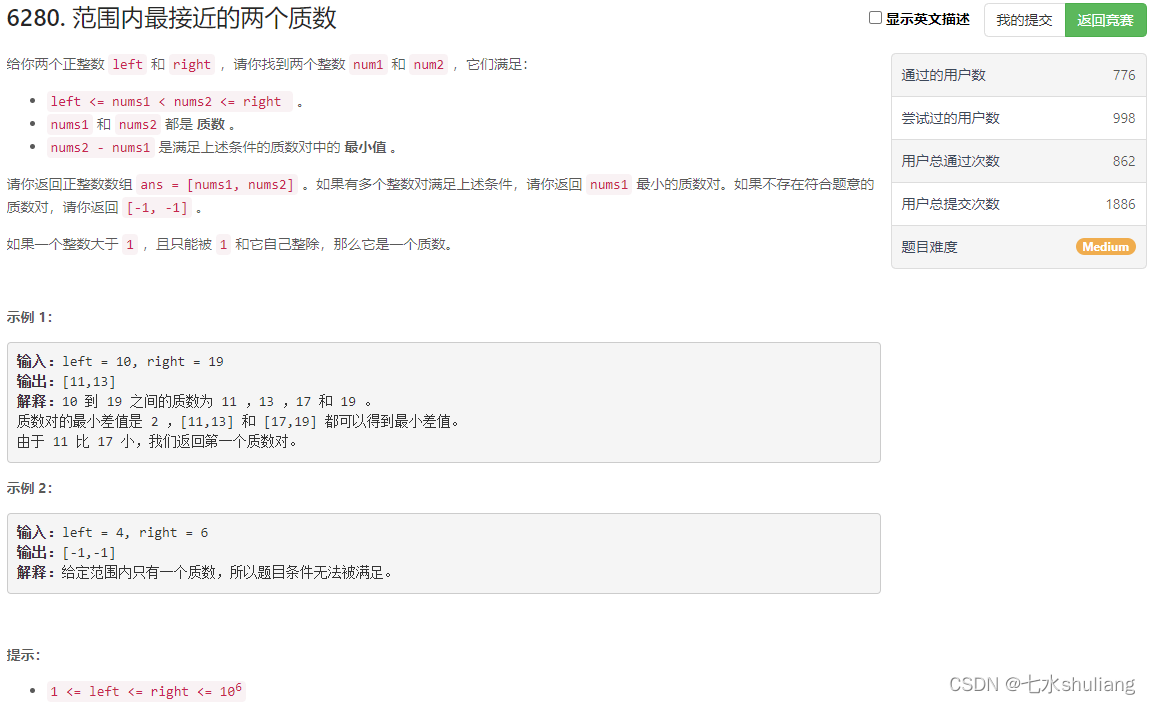
2. 思路分析

• py由于切片的存在，埃氏筛表现超过线性筛。
• 预处理质数并提取出来ps=[2,3,5,7,11…]
• 计算时用二分切片出来左右范围，然后暴力pairwise判断即可。

3. 代码实现

def tag_primes_eratosthenes(n):  # 返回一个长度n的数组p，如果i是质数则p[i]=1否则p[i]=0
    primes = [1]*n
    primes[0] = primes[1] = 0  # 0和1不是质数
    for i in range(2,int(n**0.5)+1):
        if primes[i]:
            primes[i * i::i] = [0] * ((n - 1 - i * i) // i + 1)
    return primes
primes = tag_primes_eratosthenes(10**6+5)
ps = [i for i,v in enumerate(primes) if v]

class Solution:
    def closestPrimes(self, left: int, right: int) -> List[int]:
        x = bisect_left(ps,left)
        y = bisect_right(ps,right)
        if y-x<2:
            return [-1,-1]
        ans = (inf,0,0)
        for a,b in pairwise(ps[x:y]):
            if (b-a,a,b)<ans:
                ans = (b-a,a,b)
        return [ans[1],ans[2]]        

六、参考链接