一、问题描述

二、DFS暴搜

1、算法思路

这道题其实最容易想到的是暴力DFS，然后选出一个最大值。我们平时会在DFS的形参中设置一个变量表示子树的根。但是今天这道题还涉及到你是否选当前的形参中的根节点。

凡是用DFS，我们都要明确这个函数的作用，而明确了作用之后，我们才方便写递归。

我们这里的DFS函数的作用就是：

在根节点选或者不选的条件下，分别计算出子树中的快乐指数的最大值。

2、代码实现

#include<iostream>
#include<cstring>
using namespace std;
const int N=60010,M=3*N;
int hap[N];
int h[N],e[M],ne[M],idx;
int n;
void add(int x,int y)
{
    e[idx]=y,ne[idx]=h[x],h[x]=idx++;
}
int dfs(int u,int x)
{
    if(h[u]==-1)return 0;
    int ans=0;
    if(!x)
        for(int i=h[u];i!=-1;i=ne[i])
            ans+=max(dfs(e[i],0),dfs(e[i],1)+hap[e[i]]);
    else
        for(int i=h[u];i!=-1;i=ne[i])
            ans=ans+dfs(e[i],0);
    return ans;
}
int main()
{
    memset(h,-1,sizeof h);
    cin>>n;
    for(int i=1;i<=n;i++)scanf("%d",hap+i);
    int r=1;//r是用来寻找根节点的
    for(int i=0;i<n-1;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(b,a);
        if(a==r)r=b;
    }
    int res=max(dfs(r,0),dfs(r,1)+hap[r]);
    cout<<res<<endl;
    return 0;
}

这种方法非常好想，但是效率非常的慢，已经超时了。

为什么慢？因为很多问题出现了重复搜索的现象，我们以样例为例子：（我们输出调用函数时的形参）

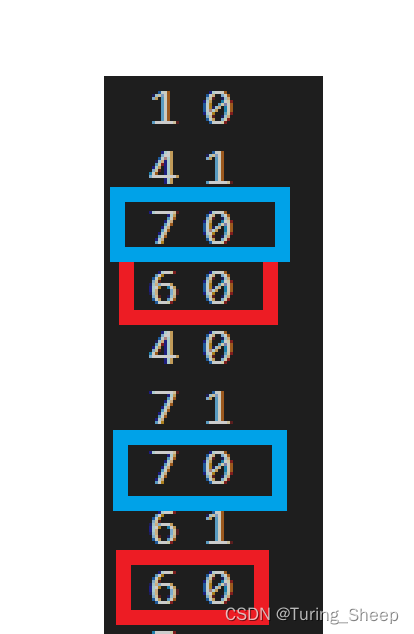
我们发现，一个如此简单的样例，里面都有2组函数发生了两次重复。当数据量增大的时候，重复的次数会非常多。

三、DP做法

这次我们换一种方式，为了解决DFS重复计算的问题，我们可以采用随搜随记的方式来记录。这样的话，我们可以直接查表，但是不管怎么样，都需要遍历一遍二叉树，但是我们优化之后可以保证只遍历一次。

那么我们就用$f[u][2]$来记录。

#include<iostream>
#include<cstring>
using namespace std;
const int N=6010;
int n;
int h[N],e[N],ne[N],idx;
int hap[N];
int f[N][2];
void dfs(int u)
{
    f[u][1]=hap[u];
    for(int i=h[u];i!=-1;i=ne[i])
    {
        dfs(e[i]);
        f[u][0]+=max(f[e[i]][1],f[e[i]][0]);
        f[u][1]+=f[e[i]][0];
    }
}
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int main()
{
     scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &hap[i]);
    memset(h, -1, sizeof h);
    int root=1;
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(b, a);
        if(a==root)root=b;
    }
    dfs(root);
    cout<<max(f[root][0],f[root][1]);
    return 0;
}