题目描述
Farmer John 最近购入了 N 头新的奶牛,每头奶牛的品种是更赛牛(Guernsey)或荷斯坦牛(Holstein)之一。
奶牛目前排成一排,Farmer John 想要为每个连续不少于三头奶牛的序列拍摄一张照片。
然而,他不想拍摄这样的照片,其中只有一头牛的品种是更赛牛,或者只有一头牛的品种是荷斯坦牛——他认为这头奇特的牛会感到孤立和不自然。
在为每个连续不少于三头奶牛的序列拍摄了一张照片后,他把所有「孤独的」照片,即其中只有一头更赛牛或荷斯坦奶牛的照片,都扔掉了。
给定奶牛的排列方式,请帮助 Farmer John 求出他会扔掉多少张孤独的照片。
如果两张照片以不同位置的奶牛开始或结束,则认为它们是不同的。
输入格式
输入的第一行包含 N。
输入的第二行包含一个长为 N 的字符串。如果队伍中的第 i 头奶牛是更赛牛,则字符串的第 i 个字符为 G。否则,第 i 头奶牛是荷斯坦牛,该字符为 H。
输出格式
输出 Farmer John 会扔掉的孤独的照片数量。
数据范围及示例
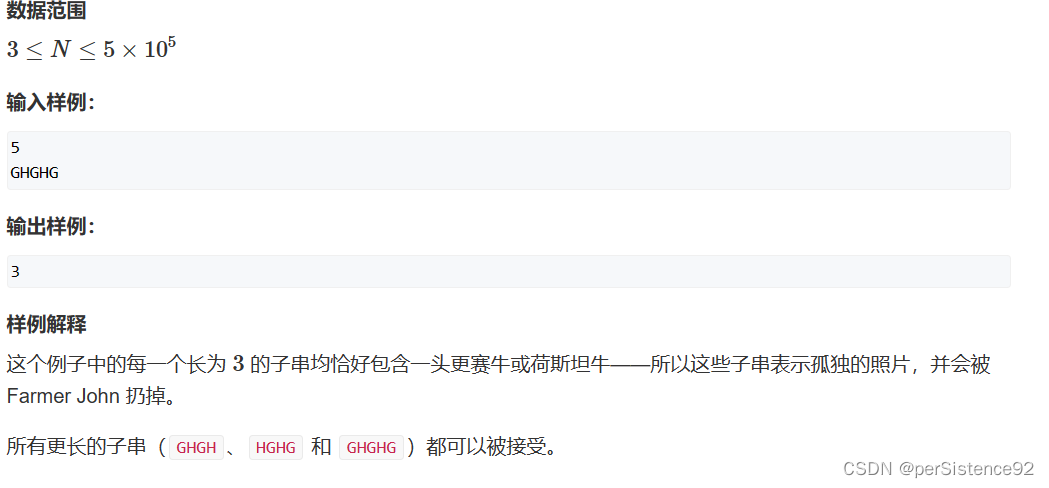
思路
作为AcWing寒假每日一题的第一题,看到这道题之后思路全无,刷题的积极性瞬间被打击了^^,参考了闫学灿老师的题解后,学习到了解决这类问题的新思路。
①首先,这道题可以被抽象为:在字符串中寻找只包含一个单独字母(即,满足条件的可以全由H组成,除了一个单独的G包含在其中,vice versa)的子串,且子串的长度大于等于。
②有了①的思路,便要开始寻找子串,首先可以关注到,这道题的数据范围是50W,因此我们的算法需要将时间复杂度控制在n或者nlogn之内。
③设置两个数组l和r,用来记录遍历字符串过程中当前字母左面有多少个和它不相同的连续子串,右边有多少个和它不相同的连续子串,再从头遍历l和r,利用乘法原理得到答案。
④乘法原理的妙用:即,利用组合数来解题。对于某个字符,分为三种情况:不妨设当前字符为G,与它不同的字符即为H;
- 第一种是左侧有l个H,右侧有r个H,那么当前局面贡献的答案数为
l[i] * r[i](至少有3个字符了); - 第二种是左侧没有H,右侧有r个H,r的值应该是
2~r[i],这种局面对答案的贡献书为r[i] - 1,只有一个H的情况应当被剔除; - 第三种情况则是右侧没有H,与第二种情况类似。
- 注意,下述代码中使用了
max(r[i]-1, 0)来维护最终答案,意思即是,假如左侧没有H,右侧有,则贡献答案,否则,即如果没有,不能加负一,因此需要和0比大小。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 5;
int n;
int l[maxn] = {0}, r[maxn] = {0};
char str[maxn];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n;
cin>>str+1;
for(int i=1,h=0,g=0;i<=n;i++){
if(str[i] == 'H') l[i] = g, g = 0, h ++;
else l[i] = h, h = 0, g ++;
}
for(int i=n,g=0,h=0;i>=1;i--){
if(str[i] == 'H') r[i] = g, g = 0, h ++;
else r[i] = h, h = 0, g ++;
}
ll res = 0;
for(int i=1;i<=n;i++){
res += (ll)r[i] * l[i] + max(r[i] - 1, 0) + max(l[i] - 1, 0);
}
cout<<res;
return 0;
}