目录
一组合总和
二组合总和
三子集
四全排列
五解数独
一组合总和
题目描述:
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。

class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void _combinationSum3(int k,int n,int sum,int starti)
{
if(sum>n) //若sum已经大于n,则后面不会有满足的情况了。
return;
if(path.size()==k)
{
if(sum==n)
result.push_back(path);
return;
}
//一定要有k个数,共9个数。所以path.size()+9-i+1>=k;
for(int i=starti;i<=9-(k-path.size())+1;i++)
{
path.push_back(i);
_combinationSum3(k,n,sum+i,i+1); //数没有重复,每次i+1
path.pop_back();
}
}
vector<vector<int>> combinationSum3(int k, int n) {
_combinationSum3(k,n,0,1);
return result;
}
};二组合总和
题目描述:
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
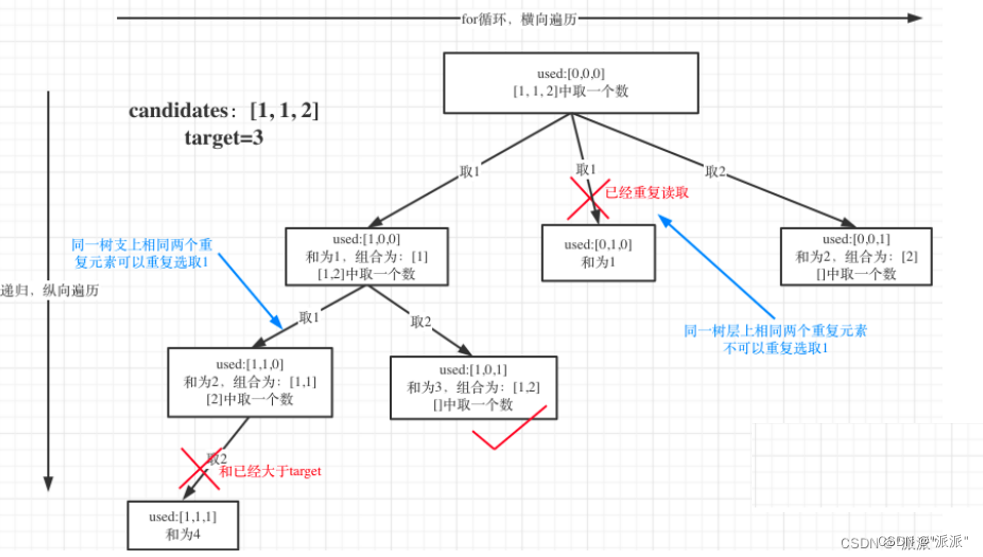
代码:
class Solution {
public:
void _combina(vector<int>& candidates,int target,vector<vector<int>>& result,
vector<int>& path,int sum,int starti)
{
if(sum==target)
{
result.push_back(path);
return;
}
if(sum>target)
return;
for(int i=starti;i<candidates.size()&&sum+candidates[i]<=target;i++)
{
if(i>starti&&candidates[i]==candidates[i-1])
continue;
sum+=candidates[i];
path.push_back(candidates[i]);
_combina(candidates,target,result,path,sum,i+1);
sum-=candidates[i];
path.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<vector<int>> result;
vector<int> path;
sort(candidates.begin(),candidates.end());
int sum=0;
_combina(candidates,target,result,path,sum,0);
return result;
}
};三子集
题目描述:
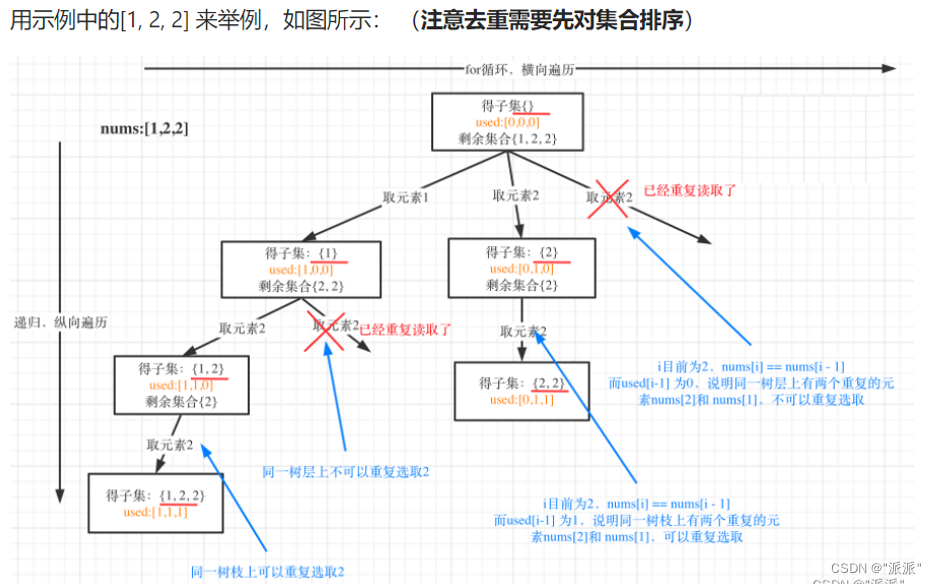
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
与上一题几乎完全一样:
代码:
class Solution {
public:
void _subsets(vector<vector<int>>& result,vector<int>& path,vector<int>&nums,int starti)
{
result.push_back(path);
if(starti==nums.size())
return;
for(int i=starti;i<nums.size();i++)
{
if(i>starti&&nums[i]==nums[i-1])
continue;
path.push_back(nums[i]);
_subsets(result,path,nums,i+1);
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(),nums.end());
vector<vector<int>>result;
vector<int> path;
_subsets(result,path,nums,0);
return result;
}
};四全排列
题目描述:给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
例如:
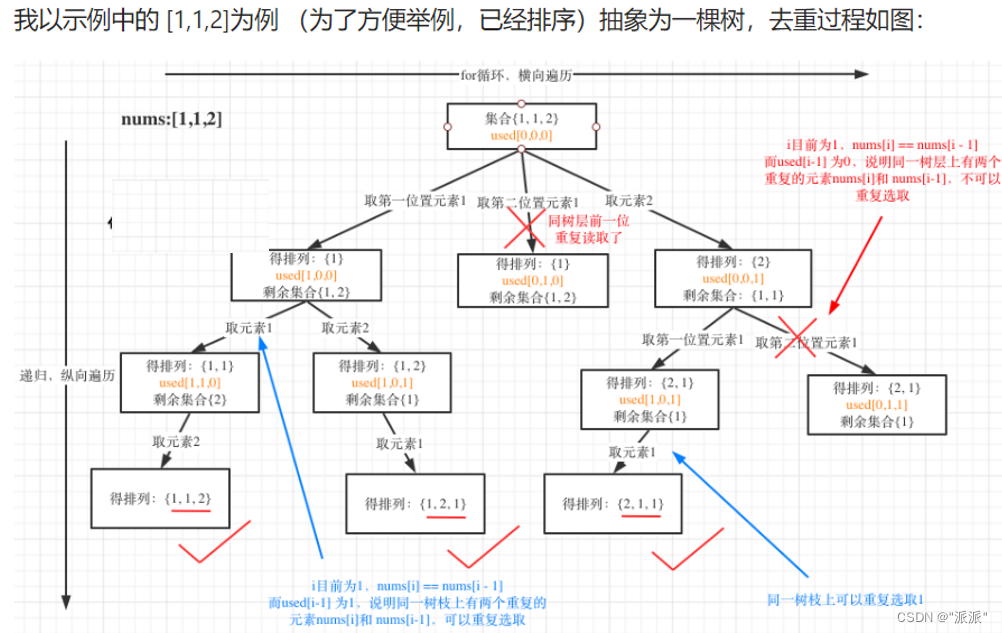
输入:nums = [1,1,2] 输出:[[1,1,2],[1,2,1], [2,1,1]]
用一个used数组来标识数字是否被访问过。
代码:
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void _permuteUnique(vector<int>& nums,vector<bool>& used)
{
if(path.size()==nums.size())
{
result.push_back(path);
return;
}
for(int i=0;i<nums.size();i++)
{
if(used[i]==false||(i>0&&nums[i]==nums[i-1]&&used[i-1]==true))//去重判断
continue;
path.push_back(nums[i]);
used[i]=false;
_permuteUnique(nums,used);
path.pop_back();
used[i]=true;
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<bool> used;
used.resize(nums.size(),true);
sort(nums.begin(),nums.end());
_permuteUnique(nums,used);
return result;
}
};五解数独

代码:
思路:遍历每一个位置,若这个位置为空,则开始放置合适的数字(1-9),若果找到了合适的数字,把数字放入后,开始去遍历下个数字,重复操作。若果在这一个空的位置里面没有找到合适的数字,那么返回上一个之前为空的位置,重新放入合适的位置,再去遍历下一个位置。注意程序结束时的返回条件
class Solution {
private:
bool backtracking(vector<vector<char>>& board)
{
for (int i = 0; i < board.size(); i++) { //两层for循环遍历每一个位置
for (int j = 0; j < board[0].size(); j++)
{ // 遍历列
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) //放入合适的数字1-9
{
if (isValid(i, j, k, board))
{
board[i][j] = k;
if (backtracking(board)) //继续寻找下一个合适的位置
return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; //说明下一个空位没有找到合适数字,当前要重新放置数字
}
}
return false; //在一个空位上没找到合适位置,返回false.
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for (int i = 0; i < 9; i++) { // 判断行里是否重复
if (board[row][i] == val) {
return false;
}
}
for (int j = 0; j < 9; j++) { // 判断列里是否重复
if (board[j][col] == val) {
return false;
}
}
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
for (int j = startCol; j < startCol + 3; j++) {
if (board[i][j] == val ) {
return false;
}
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};这种写法也一样:
int flag=0;
void backtracking(vector<vector<char>>& board)
{
for (int i = 0; i < board.size(); i++)
{
for (int j = 0; j < board[0].size(); j++)
{
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++)
{ // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board))
{
board[i][j] = k; // 放置k
backtracking(board);
if(flag==1) //falg==1,说明已找到一组,回溯时直接返回,不用继续寻找
return;
board[i][j] = '.'; // 回溯,撤销k
}
}
return; // 9个数都试完了,都不行,那么返回给上一层
}
}
flag=1; //说明棋盘已放满
}