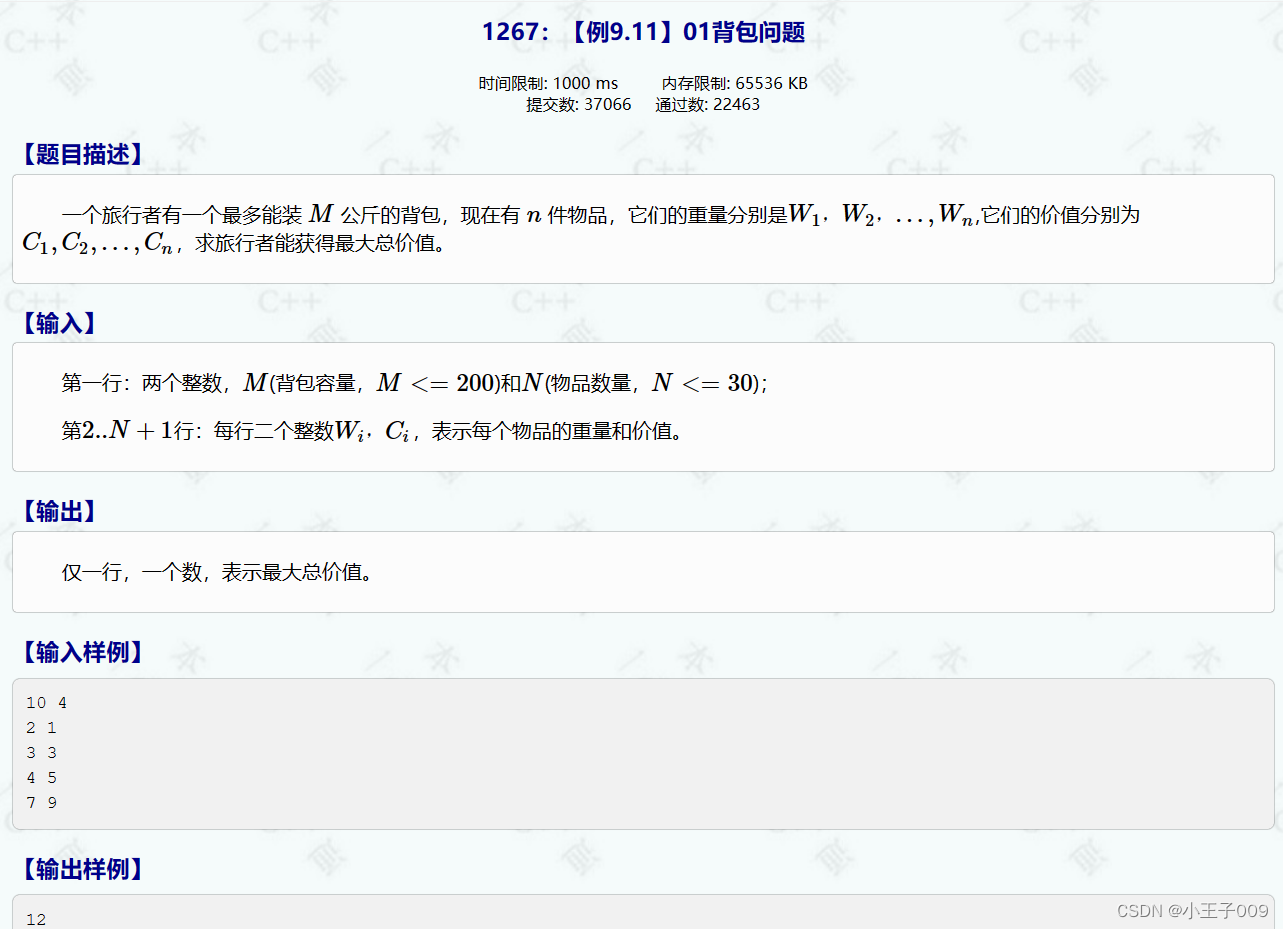
经典01背包问题
这里给你3种方法
目录
DFS
思路:
代码:
DFS+记忆化
思路:
代码:
动态规划
思路:
代码:
DFS
时间复杂度 :O(2^n)
思路:
DFS求出所有选法,再用ans记录价格最大值
由于此题数据量较小(其实2^30=1073741824,这种做法是过不了的,是题目数据比较水^_^)
代码:
//【例9.11】01背包问题
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 35;
int n, m, ans;//n 容量 m 物品
int w[N], v[N]; //w 第i件物品的重量(代价) v 第i件物品的价值
//idx 物品编号 resw 背包剩余容量 sumv 当前决策下的总价值
void dfs(int idx, int resw, int sumv) {
if (idx == n + 1) {
ans = max(ans, sumv);
return ;
}
//不选
dfs(idx + 1, resw, sumv);
//选
if (resw >= w[idx])
dfs(idx + 1, resw - w[idx], sumv + v[idx]);
}
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i ++)
cin >> w[i] >> v[i];
dfs(1, m, 0);
cout << ans;
return 0;
}
/*
【输入样例】
10 4
2 1
3 3
4 5
7 9
【输出样例】
12
*/如果在考试遇到这种01背包题目DFS是肯定拿不了满分的
DFS+记忆化
时间复杂度:O(nm)
针对上一个做法 纯·DFS 有可能会超时的情况我们推出了加上记忆化的版本
思路:
我们分析一下为什么 纯·DFS 做法会超时
我们用一个小样例自己推一下
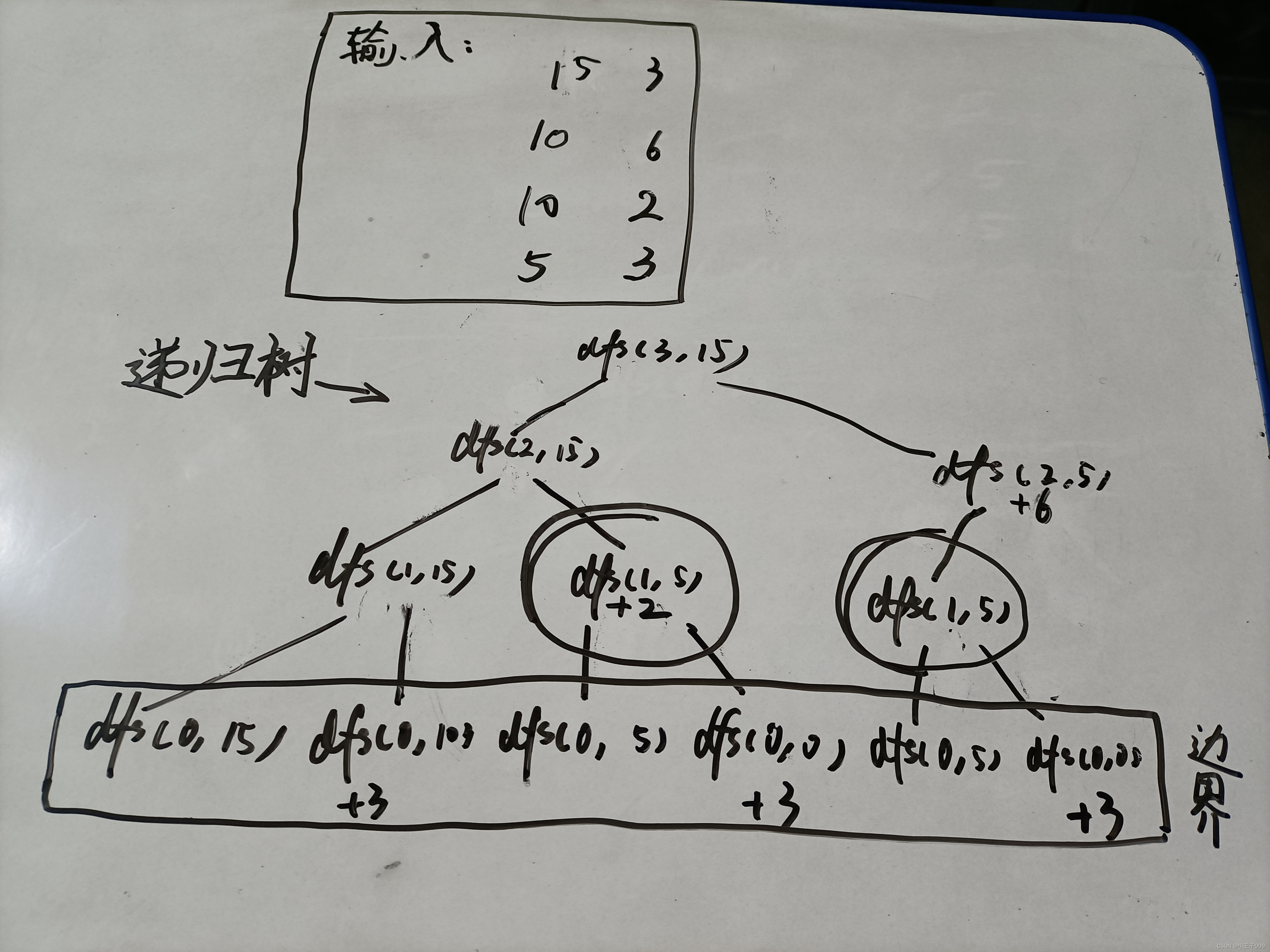
先不管答案是什么,我们发现dfs(1, 5)出现了多次
如果样例再大一点就会有很多重复子问题
重复子问题 ?想到什么了?对了,用记忆化存储状态!
只要在上一种方法的代码加上一个二维dp数组存储状态就能起到优化时间复杂度的作用
dp[i][j] 代表 用前i件物品来装容量为j的背包所能得到的最大价值
代码:
//【例9.11】01背包问题
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 35, M = 205;
int n, m;//n 容量 m 物品
int w[N], v[N]; //w 第i件物品的重量(代价) v 第i件物品的价值
/*
idx 物品编号 resw 背包剩余容量
如果
第i件物品不选
dfs(i, j) = dfs(i - 1, j)
第i件物品选
dfs(i, j) = dfs(i - 1, j - w[i]) + v[i]
*/
int dp[N][M];
int dfs(int idx, int resw) {
//用前i件物品来装容量为j的背包所能得到的最大价值
if (!idx)
return 0;
if (dp[idx][resw] != -1)
return dp[idx][resw];
//不选
int maxn = dfs(idx - 1, resw);
//选
if (resw >= w[idx])
maxn = max(maxn, dfs(idx - 1, resw - w[idx]) + v[idx]);
return dp[idx][resw] = maxn;
}
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i ++)
cin >> w[i] >> v[i];
memset(dp, -1, sizeof dp);
cout << dfs(n, m);
return 0;
}
/*
【输入样例】
10 4
2 1
3 3
4 5
7 9
【输出样例】
12
*/动态规划
时间复杂度:O(nm)
思路:
其实也就是把 DFS+记忆化 改成递推形式,在上一种方法的代码里也已经透露了状态转移方程
第i件物品不选
dp[i, j] = dp[i - 1, j]
第i件物品选
dp[i, j] = dp[i - 1, j - w[i]] + v[i]代码:
//【例9.11】01背包问题 O(nm)
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 35, M = 205;
int n, m;//n 容量 m 物品
int w[N], v[N]; //w 第i件物品的重量(代价) v 第i件物品的价值
int dp[N][M];
int main() {
cin >> m >> n;
for (int i = 1; i <= n; i ++)
cin >> w[i] >> v[i];
/*
dp[i, j] 用前i件物品来装容量为j的背包所能得到的最大价值
第i件物品不选
dp[i, j] = dp[i - 1, j]
第i件物品选
dp[i, j] = dp[i - 1, j - w[i]] + v[i]
*/
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= m; j ++) {
dp[i][j] = dp[i - 1][j]; //不选
if (j >= w[i]) //可选
dp[i][j] = max(dp[i][j], dp[i - 1][j - w[i]] + v[i]);
}
}
cout << dp[n][m];
return 0;
}
/*
【输入样例】
10 4
2 1
3 3
4 5
7 9
【输出样例】
12
*/代码可以拿走,请把赞留下
原题链接:信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn)