目录
算法
算法概述
算法复杂度
数据结构
数据结构的概述
物理结构
逻辑结构
简单排序
1.选择排序
1.1算法描述
1.2算法实现
2冒泡排序
2.1算法描述
2.2算法实现
3插入排序
3.1算法描述
3.2算法实现
三种算法的比较
算法
算法概述
算法是一系列程序指令,用于处理特定的运算和逻辑问题
也可以理解成,输入一个数据,通过算法可以获取需要的输出结果
算法复杂度
算法是有优劣之分的,通过时间复杂度和空间复杂度进行区别。
时间复杂度:是一个算法运行时间长度的一个度量,用大O表示。
1.常见的时间复杂度按照从低到高的排序,包括:O(1) < O(logn) < O(n) <O(nlogn) < O(n2)等
2.不同的时间复杂度的差异

3.空间复杂度:是指一个算法在运行过程中临时占用内存空间大小的度量,用大O表示。
很多时候,我们不得不在时间和空间复杂度之间做取舍。有时我们需要牺牲时间来换取空间,有时
候我们需要牺牲空间换取时间。绝大多数时候,时间复杂度更重要一些,存储空间不足可以进行扩
充,但是程序的执行速度是必须要放在首位的。
数据结构
数据结构的概述
数据结构是数据的组织、管理和存储格式,其使用目的是为了高效的修改和访问数据。
数据结构可以分为物理结构和逻辑结构
物理结构
物理结构就是计算机中真实的存储方式,主要是有数组和链表两种
1.数组存储就是将数据存放在连续内存空间中:

2.链表存储可以将数据存放在内存的任意位置,每个通过指向下一个元素的指针实现

逻辑结构
逻辑结构就是从具体问题抽象出来的模型,是抽象意义上的结构,可以按照对象中的元素之间的关
系相互分两类。
常见的逻辑结构有以下几种:
1.线性结构(按照顺序排列)
2.树结构(层次结构)
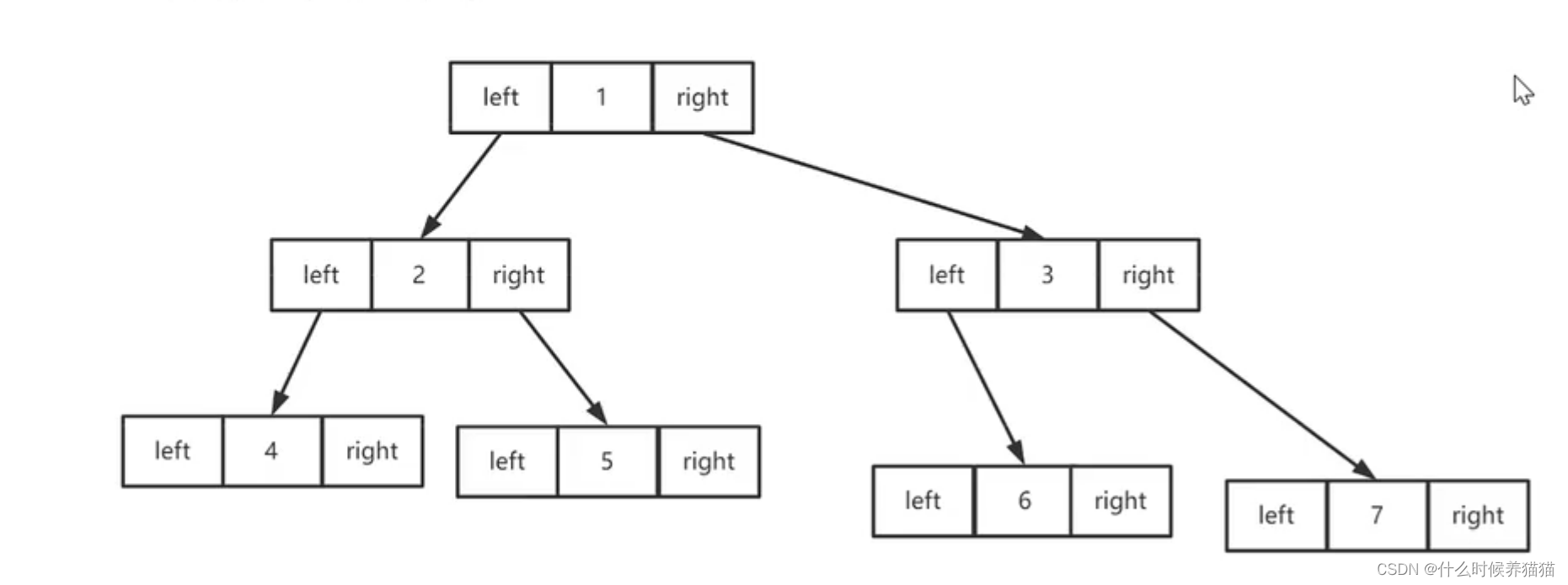
注:每一个元素只有一个父类元素。
3.图结构(网状结构)
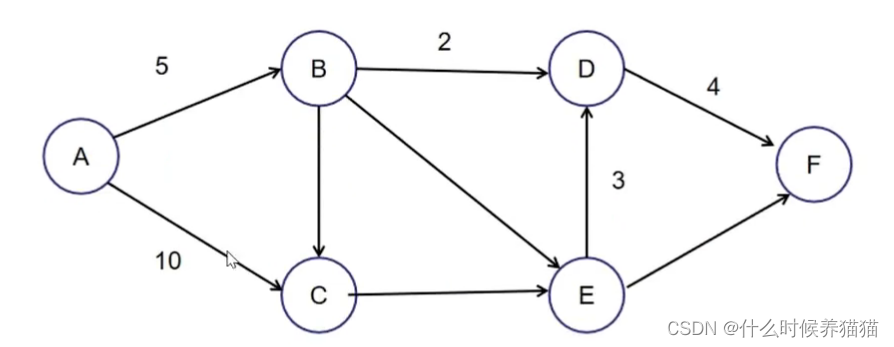
任何逻辑结构都是通过两种物理结构数组和链表进行实现,而在代码的编写过程中,野火设计一些抽象数据类(Abstract Data Type),来完成添加、删除以及遍历等这样的操作。
简单排序
1.选择排序
1.1算法描述
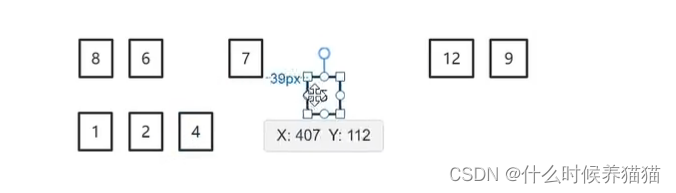
首先在未排序的序列中找到最小(大)元素,存放到排序序列的起始位置,
然后,再从剩余为排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
以此类推,直到所有元素均排序完毕。
1.2算法实现
分解1:从未排序的数组中,找到最小的元素

分解2:将最小值和未排序的数组的第一个元素进行交换


分解3:将未排序的数组分别重复分解1和分解2的操作,每次数组的起始位置增加,指导排序完毕。


分解4:使用循环操作代替Start


实操:
package SelectionSort;
public class SelectionSort001 {
public static void main(String[] args) {
int[] arrs ={8,6,1,7,2,5,4,12,9};
//存储最小值所在的位置
int minPos = 0;
//遍历数组找到最小的数字
for(int i = 0;i <arrs.length;i++){
if(arrs[minPos] > arrs[i]){
//保存最小值所在的位置
minPos = i ;
}
}
System.out.println("最小的数字为"+arrs[minPos]);
//交换
int temp = arrs[0];
arrs[0] = arrs[minPos];
arrs[minPos] = temp;
//输出结果
for(int i = 0; i < arrs.length;i++){
System.out.println(arrs[i]+",");
}
}
}
将数组中最小/最大的元素放在首位,找到它所在的下标,将首位元素交换到其位置。
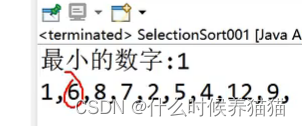
第二轮就需要改变循环开始的位置,将minPos=1;

我们可以总结规律:
package SelectionSort;
public class SelectionSort001 {
public static void main(String[] args) {
int[] arrs ={8,6,1,7,2,5,4,12,9};
for(int j = 0; j < arrs.length ; j++){
int minPos = j;
//遍历数组找到最小的数字
for(int i = j+1; i <arrs.length; i++){
if(arrs[minPos] > arrs[i]){
//保存最小值所在的位置
minPos = i ;
}
}
System.out.println("最小的数字为"+arrs[minPos]);
//交换
int temp = arrs[j];
arrs[j] = arrs[minPos];
arrs[minPos] = temp;
}
//输出结果
for(int i = 0; i < arrs.length;i++){
System.out.println(arrs[i]+",");
}
}
}
2冒泡排序
2.1算法描述
首先在未排序数组的首位开始,和后面相邻的数字进行比较,如果前面一个比后面一个大那么则进行交换。
接下来再讲第二个位置的数字和后面相邻的数字进行比较,如果大那么则进行交换,直到讲最大的数字交换到数组的尾部
然后再从排序的首位开始,重复前面两部分讲最大的数字交换到数组的尾部(交换到尾部的数字是已经排好序的)。
2.2算法实现
分解1:将第一个数字和后面的相邻的数字进行比较,如果大则进行交换

分解2:通过比较交换,将最大的数字交换到数组的尾部

分解3:重复执行分解1和分解2,将最大的数字交换到未排序数组的尾部,直到排序完成


分解4:利用循环代替重复的操作

实操:
package Sort;
public class BubbleSort002 {
public static void main(String[] args) {
int[] arrs ={8,6,1,7,2,5,4,12,9};
for(int j=1 ; j < arrs.length ;j++){
for(int i = 0;i < arrs.length - j;i++){
//比较两个元素
if(arrs[i]>arrs[i+1]){
int temp = arrs[i];
arrs[i] = arrs[i+1];
arrs[i+1] = temp;
}
}
}
//输出结果
for(int i = 0; i < arrs.length;i++){
System.out.println(arrs[i]+",");
}
}
}
3插入排序
3.1算法描述


 1.从第一个元素开始,该元素可以认为已经被排序;
1.从第一个元素开始,该元素可以认为已经被排序;
2.取出下一个元素,在已经排序的元素序列中从后往前扫描;
3.如果该元素(已排序)大于新元素,将该元素移到下一个位置;
4.重复步骤3,直到找到已排序的元素小于或等于新元素的位置;
5.将新元素插入到该位置后;
6.重复步骤2~5;
3.2算法实现
分解1:从未排序的数组中取出第一个元素,和已排序的集合中的元素进行比较,则将被比较的元素向后移动直到数组的头部或者找到比前面的比取相互元素要小的位置

分解2:重复分解1的操作,逐步扩展已排序好队列。




分解3:使用循环操作优化每一轮寻找插入位置的操作





分解4:使用循环操作优化多轮的插入操作


代码:
package Sort;
public class InsertSort003 {
public static void main(String[] args) {
int[] arrs ={8,6,1,7,2,5,4,12,9};
for(int start=1;start < arrs.length;start++){
int insert = arrs[start];//待插入的元素
while (start > 0){
if(arrs[start-1]>insert){
//前面的数字比待插入的数字大,就把前面的数字往后移
arrs[start - 1]=arrs[start];
}else{
arrs[start]= insert;
//终止循环
break;
}
start--;
}
//如果start=0直接注入到首位
if(start == 0){
arrs[0]=insert;
}
}
//输出结果
for(int i = 0; i < arrs.length;i++){
System.out.println(arrs[i]+",");
}
}
}三种算法的比较
1.上面的三种排序,冒泡、选择、插入由于军使用了嵌套循环,并且循环基本上要遍历所有的元素,所以用大O表示法需要(N^2)时间级别
2.但是三种排序还是有一些细微的区别(循环次数、交换次数)
冒泡排序的书写最为简单,但是平均性能没有选择和插入排序的好。因为它的循环次数和交换次数比较多。
选择排序循环比较的次数多,但是交换的次数少
插入排序的交换次数多,但是循环次数少