树的基本知识

树的定义

树是由n（n>=0）个结点组成的优先集合。如果n等于0，称为空树；但如果n>0，则
1）有一个特定称为根的结点，他只有直接后继，没有直接前驱。
2）除根节点之外的其他节点分为m（m>=0）个互不相交的有限集合，每个集合又是一棵树，并且称之为根的子树。每个子树的根结点有且只有一个直接前驱，但是可以有0个或多个直接后继。

树的基本概念

1.节点的度：一个结点含有子树的个数称为该结点的度
2.树的度：一棵树中，最大的结点的度称为树的度
3.叶节点或终端结点：度为0的结点
4.非终端结点或分支节点：度不为0的结点
5.父亲节点或父节点：若一个结点含有子节点，则称这个结点为其子节点的父节点
6.孩子节点或子节点：一个结点含有的子树的根结点称为该结点的子节点
7.兄弟节点：具有相同父节点的结点互称为兄弟结点
8.结点层次：从根开始定义起，根为第一层，根的子节点为第二层，以此类推
9.深度：对于任意节点n，n的深度为从根到n的唯一路径长，根的深度为0
10.高度：对于任意结点n，n的高度为从n到一篇树叶的最长路径长，所有的树叶的高度为0
11.堂兄弟结点：父节点在同一层上的结点互为堂兄弟
12.结点的祖先：从根节点到该结点所经分支上的所有结点
13.子孙：以某节点为根的子树中任意一个结点都称之为该结点的子孙
14.森林：由m（m>=0）棵互不相交的树的集合称之为森林
15.树中任意节点的子节点之间没有顺序关系，这种树称之为无序树，也叫自由树，反之为有序树

二叉树的性质

• 二叉树不同于树的特点是由一个根节点和两颗互不相交的，分别称为根节点的左子树和右子树的二叉树组成。
• 若二叉树的层次从0开始，则二叉树的第i层最多有2^i个结点
• 高度为k的二叉树，最多有2^(k+1)+1个结点
• 对于任意一棵二叉树，如果叶子节点个数为n0，度数为2的非叶子结点个数为n2，则有n0=n2+1
• 满二叉树：每一层的结点树都达到了最大值，则这个二叉树就是满二叉树
• 完全二叉树：一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。
• 具有n个结点的完全二叉树的高度为[log 2^(n+1)]-1.
  如果一棵树的左孩子和右孩子都是一颗满二叉树，那么他本身不一定是一颗满二叉树
  如果一棵树的左孩子和有孩子都是一棵完全二叉树，那么它本身也不一定是一棵完全二叉树

二叉树的存储表示

顺序存储（数组存储）

只适合存储满二叉树或者完全二叉树，否则就会存在空间浪费。

链式表示

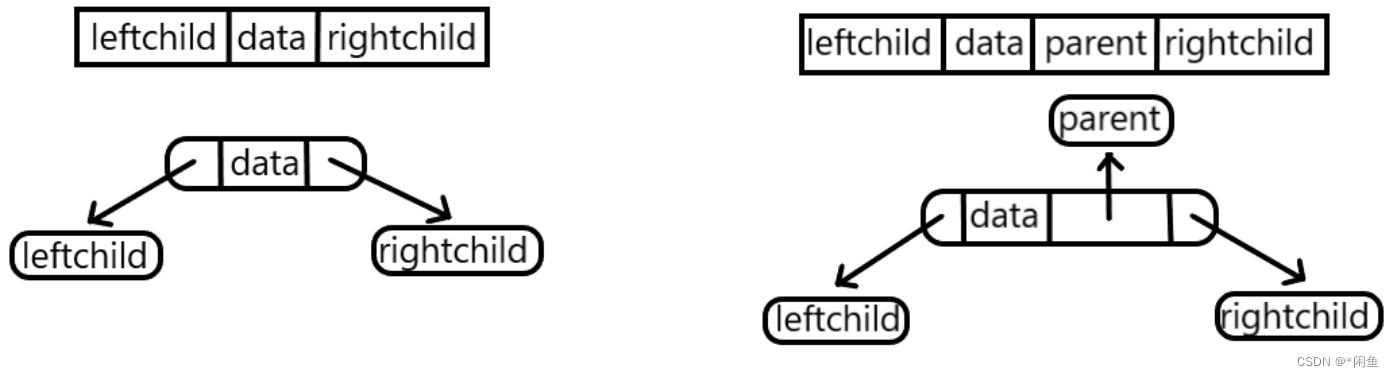
这两类差别在于是否存在双亲指针，可以通过双亲指针快速回溯。

二叉链表的静态结构（静态存储）

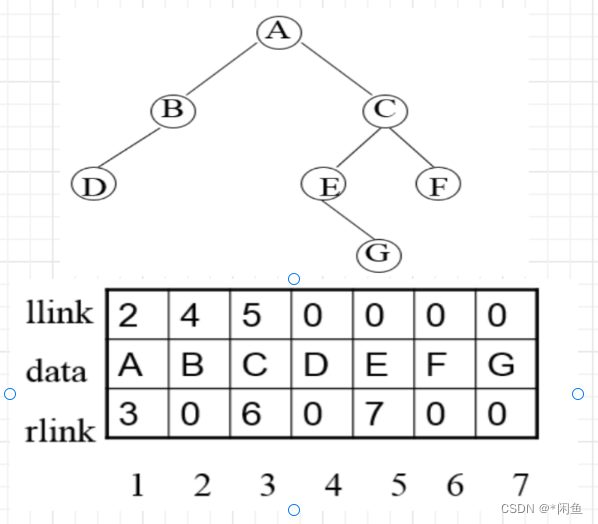
llink表示左孩子，rlink表示有孩子，表格中的数据表示下标0表示不存在。例如A结点，左孩子下标为2，2号结点为B，右孩子为3号下标的C结点，所以A结点的左孩子为B，右孩子为C。

结构体设计

//三叉链表
typedef char ElemType;
typedef struct BtNode{
struct BtNode *leftchild;
struct BtNode *parent;
struct BtNode *rightchild;
ElemType data;
}BtNode,*BinaryTree;
//二叉链表
typedef char ElemType;
typedef struct BtNode{
struct BtNode *leftchild;
struct BtNode *rightchild;
ElemType data;
}BtNode,*BinaryTree;

二叉树的遍历

遍历思路

遍历的三种顺序：
先序：根左右
中序：左根右
后序：左右根
遍历规则：因为三种顺序遍历规则大同消息，此处用中序举例
1）若二叉树为空，则结束，
2）否则按顺序访问左子树 ，根节点，右子树。

我们以上图中的树做一中序遍历进行举例：首先从根节点开始遍历根结点A，接着遍历左孩子，左孩子又当作一整棵树，按根左右的顺序进行遍历，先遍历根节点B，下来遍历左孩子，把他整体看成一棵树，先根节点D，没有左右节点，开始回溯，B结点没有右节点又开始回溯到根节点，开始 遍历根节点的右孩子，同左孩子一样，把其右孩子当作一整棵树，先遍历根节点C，接着左孩子的根节点E，E没有左孩子，开始遍历右孩子G，G为叶子节点所以回溯，回溯到C，C遍历过了所以遍历其右孩子F即可结束。所以中序遍历顺序是ABDCEGF。

代码

BtNode* Buynode(){
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (nullptr == s) {
		exit(1);
	}
	memset(s, 0, sizeof(BtNode));
	return s;
}
void PreOrder(BtNode* ptr) {
	if (ptr != nullptr) {
		printf("%c ", ptr->data);
		InOrder(ptr->leftchild);
		InOrder(ptr->rightchild);
	}

}
void InOrder(BtNode* ptr) {
	if (ptr != nullptr) {
		InOrder(ptr->leftchild);
		printf("%c ",ptr->data);
		InOrder(ptr->rightchild);
	}

}
void PastOrdor(BtNode* ptr) {
	if (ptr != nullptr) {
		InOrder(ptr->leftchild);
		InOrder(ptr->rightchild);
		printf("%c ", ptr->data);
	}

}
BtNode* CreatBtStr(const char* &str) {
	BtNode* s = nullptr;
	if (*str != '#') {
		s = Buynode();
		s->data = *str;
		s->leftchild = CreatBtStr(++str);
		s->rightchild = CreatBtStr(++str);
	}
	return s;
}
BtNode* CreatTreeStr(const char* str) {
	if (nullptr == str || strlen(str) <= 0) {
		return nullptr;
	}
	else return CreatBtStr(str);
}
int main() {
	const char* str = "ABC##DE##F##G#H##";
	BinaryTree root = CreatTreeStr(str);
	PreOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PastOrdor(root);
	printf("\n");
	return 0;
}