目录
- 缓冲区和顶点属性
- 统一变量
- 顶点属性插值
- 应用变换矩阵
- 一个3D立方体示例
- 渲染一个对象的多个副本——实例化
- 在同一场景中渲染多个不同模型
- 矩阵栈
- 应对“Z冲突”伪影
- 图元的其他选项
- 性能优先的编程方法
使用 OpenGL 渲染 3D 图形通常需要将若干数据集发送给 OpenGL 着色器管线。举个例子,想要绘制一个简单的 3D 对象,比如一个立方体,你至少需要发送以下项目:
- 立方体模型的顶点;
- 控制立方体在 3D 空间中朝向的变换矩阵。
把数据发送给 OpenGL 管线还要更加复杂一点,有两种方式:
- 通过
顶点属性的缓冲区; - 直接发送给
统一变量。
理解这两种方式的机制非常重要,因为这样我们才能为每个要发送的项目选取合适的方式。
缓冲区和顶点属性
只做一次的步骤如下,它们一般包含在 init()中:
(1)创建缓冲区;
(2)将顶点数据复制到缓冲区。
每帧都要做的步骤如下,它们一般包含在 display()中:
(1)启用包含顶点数据的缓冲区;
(2)将这个缓冲区和一个顶点属性相关联;
(3)启用这个顶点属性;
(4)使用 glDrawArrays()绘制对象。
所有缓冲区通常都在程序开始的时候统一创建,可以在 init()中。在 OpenGL 中,缓冲区被包含在顶点缓冲对象(Vertex Buffer Object,VBO)中,VBO 在C++/OpenGL 应用程序中被声明和实例化。一个场景可能需要很多 VBO,所以我们常常会在 init()中生成并填充若干个 VBO,以备程序需要时直接使用。
OpenGL 中还有一种相关的结构,叫作顶点数组对象(Vertex Array Object,VAO)。 OpenGL的 3.0 版本引入了 VAO,作为一种组织缓冲区的方法,让缓冲区在复杂场景中更容易操控。 OpenGL要求至少创建一个 VAO,OpenGL要求这些数值以数组的形式指定。
假设我们想要显示两个对象。在 C++端,我们可以声明一个 VAO 和两个相关VBO(每个对象一个),就像这样:
GLuint vao[1];// OpenGL要求这些数值以数组的形式指定
GLuint vbo[2];
...
glGenVertexArrays(1, vao);// 创建 VAO,返回它的整型 ID,存进数组 vao
glBindVertexArray(vao[0]);// 将指定的 VAO 标记为“活跃”
glGenBuffers(2, vbo);// 创建 VBO,返回它们的整型 ID,存进数组 vbo
C++缓冲区 与 GLSL顶点属性 交互的特定方式:
当 glDrawArrays()执行时,缓冲区中的数据开始流动,从缓冲区的开头开始,按顺序流过顶点着色器。顶点着色器对每个顶点执行一次。 3D 空间中的顶点需要 3 个数值,所以着色器中的顶点属性常常会使用 vec3 类型接收这 3 个数值。然后,对缓冲区中的每组这 3 个数值,着色器会被调用,如下图所示。

layout (location = 0) in vec3 position;
关键字 in 意思是“输入”(input),表示这个顶点属性将会从缓冲区中接收数值。变量的名字是 position。 layout (location=0)称为“layout 修饰符”,也就是我们把顶点属性和特定缓冲区关联起来的方法。这意味着,这个顶点属性的识别号是 0,我们后面会用到。
把一个模型的顶点加载到缓冲区( VBO)的方式取决于模型的顶点数值存储在哪里。在第 6 章中,我们将会看到通常如何使用建模工具(比如 Blender 或者 Maya)创建模型、导出成标准文件格式(比如.obj)并导入 C++/OpenGL 应用程序。我们还会看到模型的顶点如何被临时计算出来,或者在管线中使用细分着色器生成。
假设我们想要绘制一个立方体,并且假定我们的立方体的顶点数据在 C++/OpenGL 应用程序中的数组中直接指定。在这种情况下,我们需要:
(a)将这些值复制到之前生成的两个缓冲区中的一个之中,为此,我们需要使用 OpenGL 的 glBindBuffer()命令将缓冲区(例如,第 0 个缓冲区)标记为“活跃”;
(b)使用 glBufferData()命令将包含顶点数据的数组复制进活跃缓冲区(这里应该是第 0 个 VBO)。
假设顶点数据存储在名为 vPositions 的浮点类型数组中, 以下 C++代码会将这些值复制到第 0 个 VBO 中:
// 标记缓冲区为“活跃”
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
// 将数组复制进活跃缓冲区
glBufferData(GL_ARRAY_BUFFER, sizeof(vPositions), vPositions, GL_STATIC_DRAW);
接下来,我们向 display()中添加代码,将缓冲区中的值发送到着色器中的顶点属性。我们通在这个例子中声明了两个缓冲区,以强调我们常常会用到多个缓冲区。 后面我们会用到额外的缓冲区来存储顶点相关的其
他信息,比如颜色。现在,我们只用到了一个声明的缓冲区,所以只声明一个 VBO 也是足够的。
我们通过以下 3 个步骤来实现:
(a)使用 glBindBuffer()命令标记这个缓冲区为“活跃”;
(b)将活跃缓冲区与着色器中的顶点属性相关联;
(c)启用顶点属性。
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);// 标记第 0 个缓冲区为“活跃”
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);// 将第 0 个属性关联到缓冲区
glEnableVertexAttribArray(0);// 启用第 0 个顶点属性
现在,当我们执行 glDrawArrays()时,第 0 个 VBO 中的数据将传输给拥有位置 0 的 layout 修饰符的顶点属性中。这会将立方体的顶点数据发送到着色器。
统一变量
要想渲染一个场景以使它看起来是 3D 的,需要构建适当的变换矩阵并将它们应用于模型的每个顶点。在顶点着色器中应用所需的矩阵运算十分有效。此外,习惯上我们会将这些矩阵从 C++/OpenGL 应用程序发送给着色器中的统一变量。
可以使用“uniform”关键字在着色器中声明统一变量。以下示例声明了用于存储 MV 矩阵和投影矩阵的变量,足够我们的立方体程序使用:
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
关键字 mat4 表示这些矩阵是 4×4 矩阵。这里我们将用来保存 MV 矩阵的变量命名为 mv_matrix,并将用来保存投影矩阵的变量命名为 proj_matrix。
将数据从 C++/OpenGL 应用程序发送到统一变量需要执行以下步骤:
(a)获取统一变量的引用;
(b)将指向所需数值的指针与获取的统一变量的引用相关联。
在我们的立方体例子中,假设链接的渲染程序保存在名为 renderingProgram 的变量中, 则以下代码会把 MV 和投影矩阵发送到两个统一变量(即 mv_matrix 和 proj_matrix)中:
mvLoc = glGetUniformLocation(renderingProgram, "mv_matrix");// 获取着色器程序中统一变量的位置
projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvMat));// 将矩阵数据发送到统一变量中
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
GLM 函数调用 value_ptr() 返回对矩阵数据的引用, glUniformMatrix4fv()需要将这些矩阵数据传递给统一变量。
统一块:
#version 430
...
struct PositionalLight {
vec4 ambient;
vec4 diffuse;
vec4 specular;
vec3 position;
}
uniform PositionalLight light;
...
void main() {
...
vec3 l = light.position - P.xyz;
...
}
顶点属性插值
相较于如何处理统一变量,了解如何在 OpenGL 管线中处理顶点属性非常重要。在片段着色器栅格化之前,由顶点定义的图元(如三角形)被转换为片段。栅格化过程会线性插值顶点属性值,以便显示的像素能无缝连接建模后的曲面。

相比之下,统一变量的行为类似于初始化过的常量,并且在每次顶点着色器调用(即从缓冲区发送的每个顶点)中保持不变。统一变量本身不是插值的,无论顶点数量有多少,变量都始终包含相同的值。
光栅着色器对顶点属性进行的插值在很多方面都很有用。稍后,我们将使用栅格化来插值颜色、纹理坐标和曲面法向量。重要的是要理解,通过缓冲区发送到顶点属性的所有值都将在管线中被进一步插值。
顶点属性还可以改为被声明为 out,这意味着它们会将值发送到管线中的下一个阶段。
OpenGL 有一个内置的 out vec4 变量:gl_Position。在顶点着色器中,我们将矩阵变换应用于传入的顶点(之前声明为位置的顶点),并将结果赋值给 gl_Position:
gl_Position = proj_matrix * mv_matrix * position;
然后,变换后的顶点将自动输出到光栅着色器,最终将相应的像素位置发送到片段着色器。
应用变换矩阵

永远不会改变的矩阵可以在 init()中构建,但那些会改变的矩阵需要在 display() 中构建,以便在每帧重建。我们假设模型是变动的、相机是可移动的,那么:
- 需要每帧为每个模型创建模型矩阵;
- 视图矩阵需要每帧创建(因为相机可以移动),但是对于在这一帧期间渲染的所有对象,它都是一样的;
- 透视矩阵只需要创建一次(在 init()中),它需要使用屏幕窗口的宽度和高度(以及所需的视锥参数),除非调整窗口大小,否则它通常保持不变。
在 display()函数中生成模型和视图矩阵,如下所示:
(1)根据所需的相机位置和朝向构建视图矩阵;
(2)对于每个模型,进行以下操作:
i.根据模型的位置和朝向构建模型矩阵;
ii.将模型和视图矩阵结合成单个 MV 矩阵;
iii.将 MV 矩阵和投影矩阵发送到相应的着色器统一变量。
一个3D立方体示例
...
#define numVAOs 1
#define numVBOs 2
Utils util = Utils();
float cameraX, cameraY, cameraZ;
float cubeLocX, cubeLocY, cubeLocZ;
GLuint renderingProgram;
GLuint vao[numVAOs];
GLuint vbo[numVBOs];
// variable allocation for display
GLuint mvLoc, projLoc;
int width, height;
float aspect;
glm::mat4 pMat, vMat, mMat, mvMat;
// 36个顶点(6x2x3:立方体每个面由2个三角形构成,每个三角形由3个顶点指定)
// 立方体中心为(0,0,0),坐标范围都是−1.0~+1.0
void setupVertices(void) {
float vertexPositions[108] = {
-1.0f, 1.0f, -1.0f, -1.0f, -1.0f, -1.0f, 1.0f, -1.0f, -1.0f,
1.0f, -1.0f, -1.0f, 1.0f, 1.0f, -1.0f, -1.0f, 1.0f, -1.0f,
1.0f, -1.0f, -1.0f, 1.0f, -1.0f, 1.0f, 1.0f, 1.0f, -1.0f,
1.0f, -1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f, -1.0f,
1.0f, -1.0f, 1.0f, -1.0f, -1.0f, 1.0f, 1.0f, 1.0f, 1.0f,
-1.0f, -1.0f, 1.0f, -1.0f, 1.0f, 1.0f, 1.0f, 1.0f, 1.0f,
-1.0f, -1.0f, 1.0f, -1.0f, -1.0f, -1.0f, -1.0f, 1.0f, 1.0f,
-1.0f, -1.0f, -1.0f, -1.0f, 1.0f, -1.0f, -1.0f, 1.0f, 1.0f,
-1.0f, -1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 1.0f, -1.0f, -1.0f,
1.0f, -1.0f, -1.0f, -1.0f, -1.0f, -1.0f, -1.0f, -1.0f, 1.0f,
-1.0f, 1.0f, -1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 1.0f, 1.0f,
1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 1.0f, -1.0f, 1.0f, -1.0f
};
glGenVertexArrays(1, vao);
glBindVertexArray(vao[0]);
glGenBuffers(numVBOs, vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertexPositions), vertexPositions, GL_STATIC_DRAW);
}
void init(GLFWwindow* window) {
renderingProgram = Utils::createShaderProgram("vertShader.glsl", "fragShader.glsl");
cameraX = 0.0f; cameraY = 0.0f; cameraZ = 8.0f;
cubeLocX = 0.0f; cubeLocY = -2.0f; cubeLocZ = 0.0f;
setupVertices();
}
void display(GLFWwindow* window, double currentTime) {
glClear(GL_DEPTH_BUFFER_BIT);
glUseProgram(renderingProgram);
mvLoc = glGetUniformLocation(renderingProgram, "mv_matrix");
projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
// 获取window窗口的帧缓冲区的大小。当窗口大小改变时,aspect参数也会变化。
glfwGetFramebufferSize(window, &width, &height);
aspect = (float)width / (float)height;
pMat = glm::perspective(1.0472f, aspect, 0.1f, 1000.0f);// FOV=60°
vMat = glm::translate(glm::mat4(1.0f), glm::vec3(-cameraX, -cameraY, -cameraZ));
mMat = glm::translate(glm::mat4(1.0f), glm::vec3(cubeLocX, cubeLocY, cubeLocZ));
mvMat = vMat * mMat;
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvMat));
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
// 第一个参数:指定要修改的通用顶点属性的索引。等于 GLSL 中的layout(location=?)的?值。
glVertexAttribPointer(0, 3, GL_FLOAT, false, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, 36);
}
int main(void) { ... }
顶点着色器:
#version 430
layout(location = 0) in vec3 position;
uniform mat4 mv_matrix;
uniform mat4 proj_matrix;
void main() {
gl_Position = proj_matrix * mv_matrix * vec4(position, 1.0);
}
片段着色器:
#versition 430
out vec4 color;
void main() {
color = vec4(1.0, 0.0, 0.0, 1.0);
}

mat<4,4,T,Q> glm::translate(mat<4,4,T,Q> const& m, vec<3,T,Q> const& v)
从3元素的向量创建一个4×4的转换矩阵。
m - 输入矩阵乘以这个平移矩阵。
v - 平移向量的坐标。
[ v x 0 0 0 0 v y 0 0 0 0 v z 0 0 0 0 1 ] = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] ( v x v y v z 1 ) \begin{bmatrix} v_x& 0& 0&0 \\ 0& v_y& 0&0 \\ 0& 0& v_z&0 \\ 0& 0& 0&1 \end{bmatrix}= \begin{bmatrix} 1& 0& 0&0 \\ 0& 1& 0&0 \\ 0& 0& 1&0 \\ 0& 0& 0&1 \end{bmatrix} \begin{pmatrix} v_x\\ v_y\\ v_z\\ 1 \end{pmatrix} vx0000vy0000vz00001 = 1000010000100001 vxvyvz1
glm::mat4 t = glm::translate(glm::mat4(1.0f), glm::vec3(vx, vy, vz));
打印变量矩阵 t 的所有值:
(可以直接对mat4对象使用和二维数组一样的方式用下标t[i][j]访问所有元素,因为ma4类重载了[]运算符)
t[0][0] == 1.0f, t[0][1] == 0.0f, t[0][2] == 0.0f, t[0][3] == 0.0f
t[1][0] == 0.0f, t[1][1] == 1.0f, t[1][2] == 0.0f, t[1][3] == 0.0f
t[2][0] == 0.0f, t[2][1] == 0.0f, t[2][2] == 1.0f, t[2][3] == 0.0f
t[3][0] == vx , t[3][1] == vy , t[3][2] == vz , t[3][3] == 1.0f
由于GLM中是按【列】组织数据的,即[m][n]:第m-1列的第n-1个元素。
常规表示法为:
1 0 0 vx
0 1 0 vy
0 0 1 vz
0 0 0 1 (刚好满足平移变换矩阵格式)
示例中vMat = glm::translate(glm::mat4(1.0f), glm::vec3(-cameraX, -cameraY, -cameraZ));
构建了一个平移变换矩阵:通过单位矩阵(由glm::mat4(1.0f)构造) 与平移向量(由glm::vec3(x, y, z)构造),构造出一个4×4平移变换矩阵。
通常,我们需要在渲染帧之前清除深度缓冲区,以便正确地进行隐藏面消除(不清除深度缓冲区有时会导致每个曲面都被移除,从而黑屏) 。默认情况下, OpenGL 中的深度值范围为 0.0~ 1.0。调用 glClear(GL_DEPTH_BUFFER_BIT)就可以清除深度缓冲区,这时程序会使用默认值(通常为 1.0)填充深度缓冲区。我们启用深度测试glEnable(GL_DEPTH_TEST)并指定希望 OpenGL 使用的特定深度测试方法glDepthFunc(GL_LEQUAL)。接下来, display()通过调用 glUseProgram()来启用着色器,在 GPU 上加载 GLSL 代码。
为立方体设置动画:
/* 在display()函数中的部分代码 */
glClear(GL_DEPTH_BUFFER_BIT);
glClear(GL_COLOR_BUFFER_BIT);
...
// 使用当前时间来计算 x 轴、 y 轴、 z 轴坐标的不同变换
tMat = glm::translate(glm::mat4(1.0f), glm::vec3(sin(0.35f*currentTime)*2.0f, cos(0.52f*currentTime)*2.0f, sin(0.7f*currentTime)*2.0f));
// 用 1.75 来调整旋转速度
rMat = glm::rotate(glm::mat4(1.0f), 1.75f*(float)currentTime, glm::vec3(0.0f, 1.0f, 0.0f));
rMat = glm::rotate(rMat, 1.75f*(float)currentTime, glm::vec3(1.0f, 0.0f, 0.0f));
rMat = glm::rotate(rMat, 1.75f*(float)currentTime, glm::vec3(0.0f, 0.0f, 1.0f));
mMat = tMat * rMat;
当顶点与矩阵相乘时,计算从右到左进行,这意味着首先完成旋转,然后才是平移。变换的应用顺序很重要,改变顺序会导致不同的行为。
渲染一个对象的多个副本——实例化
假设我们希望扩展前面的示例,以便呈现“一群”( 24 个)翻滚的立方体。
通过循环实现:
void display(GLFWwindow* window, double currentTime) {
...
for (i = 0; i < 24; i++) {
tf = currentTime + i; // tf == "time factor(时间因子) ",声明为浮点类型
...
glDrawArrays(GL_TRIANGLES, 0, 36);
}
}
通过实例化实现:
实例化(instancing)提供了一种机制,可以只用一个C++/OpenGL 调用就告诉显卡渲染一个对象的多个副本。这可以带来显著的性能优势,特别是在绘制有数千甚至数百万个对象时,例如渲染在场地中的许多花朵。
在实例化时,顶点着色器可以访问内置变量 gl_InstanceID。这是一个整数,指向当前正在处理对象的实例的序号。
由于 GLSL 不提供平移或旋转函数,并且我们无法从着色器内部调用 GLM,因此需要在 GLSL 代码中编写相关的工具函数。
顶点着色器:
#version 430
layout (location=0) in vec3 position;
uniform mat4 v_matrix;
uniform mat4 proj_matrix;
uniform float tf;
out vec4 varyingColor;
mat4 buildRotateX(float rad);
mat4 buildRotateY(float rad);
mat4 buildRotateZ(float rad);
mat4 buildTranslate(float x, float y, float z);
void main(void) {
float i = gl_InstanceID + tf;
// float a = sin(203.0 * i/8000.0) * 403.0; //when 100000 instances
// float b = cos(301.0 * i/4001.0) * 401.0;
// float c = sin(400.0 * i/6003.0) * 405.0;
float a = sin(.35 * i) * 8.0; // when 24 instances
float b = cos(.52 * i) * 8.0;
float c = sin(.70 * i) * 8.0;
mat4 localRotX = buildRotateX(1.75*i);
mat4 localRotY = buildRotateY(1.75*i);
mat4 localRotZ = buildRotateZ(1.75*i);
mat4 localTrans = buildTranslate(a, b, c);
mat4 newM_matrix = localTrans * localRotX * localRotY * localRotZ;
mat4 mv_matrix = v_matrix * newM_matrix;
gl_Position = proj_matrix * mv_matrix * vec4(position, 1.0);
varyingColor = vec4(position,1.0)*0.5 + vec4(0.5, 0.5, 0.5, 0.5);
}
mat4 buildTranslate(float x, float y, float z) {
mat4 trans = mat4( 1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
x, y, z, 1.0 );
return trans;
}
// rotation around the X axis
mat4 buildRotateX(float rad) {
mat4 xrot = mat4( 1.0, 0.0, 0.0, 0.0,
0.0, cos(rad), -sin(rad), 0.0,
0.0, sin(rad), cos(rad), 0.0,
0.0, 0.0, 0.0, 1.0 );
return xrot;
}
// rotation around the Y axis
mat4 buildRotateY(float rad) {
mat4 yrot = mat4( cos(rad), 0.0, sin(rad), 0.0,
0.0, 1.0, 0.0, 0.0,
-sin(rad), 0.0, cos(rad), 0.0,
0.0, 0.0, 0.0, 1.0 );
return yrot;
}
// rotation around the Z axis
mat4 buildRotateZ(float rad) {
mat4 zrot = mat4( cos(rad), sin(rad), 0.0, 0.0,
-sin(rad), cos(rad), 0.0, 0.0,
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0 );
return zrot;
}
片段着色器:
#version 430
in vec4 varyingColor;
out vec4 color;
void main(void) {
color = varyingColor;
}
OpenGL/C++:
...
#define numVAOs 1
#define numVBOs 1
float cameraX, cameraY, cameraZ;
GLuint renderingProgram;
GLuint vao[numVAOs];
GLuint vbo[numVBOs];
// variable allocation for display
GLuint mLoc, vLoc, projLoc, tfLoc;
int width, height;
float aspect, timeFactor;
glm::mat4 pMat, vMat, mMat, mvMat;
void setupVertices() {
float vertexPositions[108] = {...};
glGenVertexArrays(1, vao);
glBindVertexArray(vao[0]);
glGenBuffers(numVBOs, vbo);
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertexPositions), vertexPositions, GL_STATIC_DRAW);
}
void init(GLFWwindow* window) {
renderingProgram = Utils::createShaderProgram("vertShader.glsl", "fragShader.glsl");
glfwGetFramebufferSize(window, &width, &height);
aspect = (float)width / (float)height;
pMat = glm::perspective(1.0472f, aspect, 0.1f, 1000.0f);
cameraX = 0.0f; cameraY = 0.0f; cameraZ = 32.0f; // Z=32.0f when 24 instances, 420.0f when 100000 instances
setupVertices();
}
void display(GLFWwindow* window, double currentTime) {
glClear(GL_DEPTH_BUFFER_BIT);
glClearColor(0.0, 0.0, 0.0, 1.0);
glClear(GL_COLOR_BUFFER_BIT);
glUseProgram(renderingProgram);
vLoc = glGetUniformLocation(renderingProgram, "v_matrix");
projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
vMat = glm::translate(glm::mat4(1.0f), glm::vec3(-cameraX, -cameraY, -cameraZ));
glUniformMatrix4fv(vLoc, 1, GL_FALSE, glm::value_ptr(vMat));
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
timeFactor = ((float)currentTime);
tfLoc = glGetUniformLocation(renderingProgram, "tf");
glUniform1f(tfLoc, (float)timeFactor);
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glVertexAttribPointer(0, 3, GL_FLOAT, false, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArraysInstanced(GL_TRIANGLES, 0, 36, 24);// 0, 36, 24 (or 100000)
}
void window_size_callback(GLFWwindow* win, int newWidth, int newHeight) {
aspect = (float)newWidth / (float)newHeight;
glViewport(0, 0, newWidth, newHeight);
pMat = glm::perspective(1.0472f, aspect, 0.1f, 1000.0f);
}
int main(void) {
...
glfwSetWindowSizeCallback(window, window_size_callback);
init(window);
...
}

如果注释掉glViewport(0, 0, newWidth, newHeight);拖动窗口大小时模型就不会自动居中显示了。
void glViewport(GLint x, GLint y, GLsizei width, GLsizei height);
x,y - 指定视口矩形的左下角(以像素为单位)。初始值为(0,0)。
width,height - 指定视口的宽度和高度。当GL上下文第一次附着到窗口时,宽度和高度将设置为该窗口的尺寸。
设置视口(viewport)——指定x和y从标准化设备坐标(normalized device coordinates)到窗口坐标(window coordinates)的仿射变换。
标准化设备坐标NDC:是一个x、y在[-1.0…1.0],z在[0…1]的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪,不会显示在你的屏幕上。
设(Xnd, Ynd)为标准化设备坐标。然后窗口坐标(Xw,Yw)计算如下:
Xw=(Xnd + 1) × width / 2 + x
Yw=(Ynd + 1) × height / 2 + y
视口的宽度和高度会自动钳制到一个范围,该范围取决于实现。
由于Xnd、Ynd∊[-1, 1],所以Xnd+1、Ynd+1∊[0, 2],x,y取初始值(0,0),则Xw∊[0, width]、Yw∊[0, height]。这样就完成了(Xnd,Ynd)到(Xw,Yw)的“仿射”。
虽然通常并不需要重新计算透视矩阵,但是如果运行应用程序的用户调整窗口大小(例如通过拖动窗口的角落),则重新计算就是必要的。GLFW 可以配置在调整窗口大小时自动回调指定的函数。在调用 init()之前,我们将以下内容添加到了 main():glfwSetWindowSizeCallback(window, window_reshape_callback)。
在同一场景中渲染多个不同模型
#define numVAOs 1
#define numVBOs 2
float cameraX, cameraY, cameraZ;
float cubeLocX, cubeLocY, cubeLocZ;
float pyrLocX, pyrLocY, pyrLocZ;
GLuint renderingProgram;
GLuint vao[numVAOs];
GLuint vbo[numVBOs];
// variable allocation for display
GLuint mvLoc, projLoc;
int width, height;
float aspect;
glm::mat4 pMat, vMat, mMat, mvMat;
void setupVertices(void) {
float vertexPositions[108] = {...};// 立方体
float pyramidPositions[54] =// 金字塔,6个三角形(侧面4个,底面2个)
{ -1.0f, -1.0f, 1.0f, 1.0f, -1.0f, 1.0f, 0.0f, 1.0f, 0.0f, //front
1.0f, -1.0f, 1.0f, 1.0f, -1.0f, -1.0f, 0.0f, 1.0f, 0.0f, //right
1.0f, -1.0f, -1.0f, -1.0f, -1.0f, -1.0f, 0.0f, 1.0f, 0.0f, //back
-1.0f, -1.0f, -1.0f, -1.0f, -1.0f, 1.0f, 0.0f, 1.0f, 0.0f, //left
-1.0f, -1.0f, -1.0f, 1.0f, -1.0f, 1.0f, -1.0f, -1.0f, 1.0f, //LF
1.0f, -1.0f, 1.0f, -1.0f, -1.0f, -1.0f, 1.0f, -1.0f, -1.0f //RR
};
glGenVertexArrays(1, vao);// 我们需要至少 1 个 VAO
glBindVertexArray(vao[0]);
glGenBuffers(numVBOs, vbo);// 我们需要至少 2 个 VBO
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glBufferData(GL_ARRAY_BUFFER, sizeof(vertexPositions), vertexPositions, GL_STATIC_DRAW);
glBindBuffer(GL_ARRAY_BUFFER, vbo[1]);
glBufferData(GL_ARRAY_BUFFER, sizeof(pyramidPositions), pyramidPositions, GL_STATIC_DRAW);
}
void init(GLFWwindow* window) {
renderingProgram = Utils::createShaderProgram("vertShader.glsl", "fragShader.glsl");
glfwGetFramebufferSize(window, &width, &height);
aspect = (float)width / (float)height;
pMat = glm::perspective(1.0472f, aspect, 0.1f, 1000.0f);
cameraX = 0.0f; cameraY = 0.0f; cameraZ = 8.0f;
cubeLocX = 0.0f; cubeLocY = -2.0f; cubeLocZ = 0.0f;
pyrLocX = 2.0f; pyrLocY = 2.0f; pyrLocZ = 0.0f;
setupVertices();
}
void display(GLFWwindow* window, double currentTime) {
glClear(GL_DEPTH_BUFFER_BIT);
glUseProgram(renderingProgram);
mvLoc = glGetUniformLocation(renderingProgram, "mv_matrix");
projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
vMat = glm::translate(glm::mat4(1.0f), glm::vec3(-cameraX, -cameraY, -cameraZ));
// draw the cube using buffer #0:包含立方体的顶点
mMat = glm::translate(glm::mat4(1.0f), glm::vec3(cubeLocX, cubeLocY, cubeLocZ));
mvMat = vMat * mMat;
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvMat));
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, 36);
// draw the pyramid using buffer #1:包含四棱锥的顶点
mMat = glm::translate(glm::mat4(1.0f), glm::vec3(pyrLocX, pyrLocY, pyrLocZ));
mvMat = vMat * mMat;
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvMat));
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
glBindBuffer(GL_ARRAY_BUFFER, vbo[1]);
glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, 18);
}

矩阵栈


假设:太阳(金字塔)绕X轴自转,地球(大立方体)绕Y轴自转并绕太阳公转,月球(小立方体)绕Z轴自转并绕地球公转。
压入栈的第一个矩阵通常是视图矩阵。它上面的矩阵是复杂程度越来越高的 MV 矩阵,也就是说,它们应用了越来越多的模型变换。这些变换既可以直接应用,也可以先结合其他矩阵再应用。
在我们的太阳系示例中,位于视图矩阵上方的矩阵是太阳的 MV 矩阵。再向上是地球的 MV 矩阵,其由太阳的 MV 矩阵的副本和应用于其之上的地球模型矩阵变换组成。也就是说,地球的 MV 矩阵是通过将地球的变换结合到太阳的变换中而建立的。同样,月球的 MV 矩阵位于地球的 MV 矩阵之上, 并通过将月球的模型矩阵变换应用于紧邻其下方的地球的 MV 矩阵来构建。
在渲染月球之后,可以通过从栈中弹出第一个月球的矩阵(将栈顶部的矩阵恢复为地球的 MV 矩阵),然后重复月球的变换过程,来渲染第二个月球。
基本方法如下:
(1)声明栈,命名为 mvStack。
(2)当相对于父对象创建新对象时,调用 mvStack.push(mvStack.top())。
(3)应用新对象所需的变换,也就是与所需的变换矩阵相乘。
(4)完成对象或子对象的绘制后,调用 mvStack.pop()从矩阵栈顶部移除其 MV 矩阵。
请注意,太阳的自转在它自己的局部坐标空间中进行,不应影响“子对象”(此处的地球和月球)。因此,太阳的旋转被推到栈上,但是在绘制太阳之后,它必须被从栈中移除(弹出)。
地球的公转将影响月球的运动,因此被压入栈并在绘制月球时保持在那里。相比之下,它的自转是局部的,不会影响月球,因此在绘制月球之前需要从栈中弹出。
类似地,我们会将变换矩阵压入栈以实现月球的旋转(包含公转和自转)。
以下是针对地球的代码顺序:
- push()压入地球的 MV 矩阵中会影响子对象的部分;
- translate()将地球运动结合到地球的 MV 矩阵中。在这个例子中,我们使用三角函数来计算地球运动中的平移部分;
- push()压入地球的完整 MV 矩阵,也包括它的自转;
- rotate()结合地球的轴旋转(稍后会弹出,不会影响子对象);
- glm::value_ptr(mvStack.top())获取 MV 矩阵,然后将其发送到 MV 统一变量;
- 绘制地球;
- pop()将地球的 MV 矩阵从栈中移除,暴露出它下面的地球 MV 矩阵早期副本,而该副本不包括地球的自转(因此只有地球的平移会影响月球)。
void init(GLFWwindow* window) {
renderingProgram = Utils::createShaderProgram("vertShader.glsl", "fragShader.glsl");
glfwGetFramebufferSize(window, &width, &height);
aspect = (float)width / (float)height;
pMat = glm::perspective(1.0472f, aspect, 0.1f, 1000.0f);
cameraX = 0.0f; cameraY = 0.0f; cameraZ = 12.0f;
setupVertices();
}
void display(GLFWwindow* window, double currentTime) {
glClear(GL_DEPTH_BUFFER_BIT);
glClearColor(0.0, 0.0, 0.0, 1.0);
glClear(GL_COLOR_BUFFER_BIT);
glUseProgram(renderingProgram);
mvLoc = glGetUniformLocation(renderingProgram, "mv_matrix");
projLoc = glGetUniformLocation(renderingProgram, "proj_matrix");
vMat = glm::translate(glm::mat4(1.0f), glm::vec3(-cameraX, -cameraY, -cameraZ));
// 「stack」: 1.vMat
mvStack.push(vMat);
glUniformMatrix4fv(projLoc, 1, GL_FALSE, glm::value_ptr(pMat));
// ---------------------- pyramid == sun
// 「stack」: 1.vMat 2.vMat
mvStack.push(mvStack.top());
// 「stack」: 1.vMat 2.vMat*sunTMat
mvStack.top() *= glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 0.0f, 0.0f));// 太阳位置
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat
mvStack.push(mvStack.top());
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*sunRMat
mvStack.top() *= rotate(glm::mat4(1.0f), (float)currentTime, glm::vec3(1.0, 0.0, 0.0));// 太阳旋转
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvStack.top()));
glBindBuffer(GL_ARRAY_BUFFER, vbo[1]);
glVertexAttribPointer(0, 3, GL_FLOAT, false, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, 18);
// 「stack」: 1.vMat 2.vMat*sunTMat
mvStack.pop();
//----------------------- cube == planet
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat
mvStack.push(mvStack.top());
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat
mvStack.top() *= glm::translate(glm::mat4(1.0f), glm::vec3(sin((float)currentTime)*4.0, 0.0f, cos((float)currentTime)*4.0));
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat 4.vMat*sunTMat*earthTMat
mvStack.push(mvStack.top());
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat 4.vMat*sunTMat*earthTMat*earthRMat
mvStack.top() *= rotate(glm::mat4(1.0f), (float)currentTime, glm::vec3(0.0, 1.0, 0.0));
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvStack.top()));
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glVertexAttribPointer(0, 3, GL_FLOAT, false, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, 36);
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat
mvStack.pop();
//----------------------- smaller cube == moon
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat 4.vMat*sunTMat*earthTMat
mvStack.push(mvStack.top());
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat 4.vMat*sunTMat*earthTMat*moonTMat
mvStack.top() *= glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, sin((float)currentTime)*2.0, cos((float)currentTime)*2.0));
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat 4.vMat*sunTMat*earthTMat*moonTMat*moonRMat
mvStack.top() *= rotate(glm::mat4(1.0f), (float)currentTime, glm::vec3(0.0, 0.0, 1.0));
// 「stack」: 1.vMat 2.vMat*sunTMat 3.vMat*sunTMat*earthTMat 4.vMat*sunTMat*earthTMat*moonTMat*moonRMat*moonSMat
mvStack.top() *= scale(glm::mat4(1.0f), glm::vec3(0.25f, 0.25f, 0.25f));
glUniformMatrix4fv(mvLoc, 1, GL_FALSE, glm::value_ptr(mvStack.top()));
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glVertexAttribPointer(0, 3, GL_FLOAT, false, 0, 0);
glEnableVertexAttribArray(0);
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glDrawArrays(GL_TRIANGLES, 0, 36);
// 「stack」: 1.vMat
mvStack.pop(); mvStack.pop(); mvStack.pop();
// 「stack」: Empty
mvStack.pop();// the final pop is for the view matrix
}
应对“Z冲突”伪影

在渲染多个对象时, OpenGL 使用 Z-buffer 算法来进行隐藏面消除。通常情况下,通过选择最接近相机的相应片段的颜色作为像素的颜色,这种方法可决定哪些物体的曲面可见并呈现到屏幕,而位于其他物体后面的曲面不应该被渲染。
然而,有时候场景中的两个物体表面重叠并位于重合的平面中,这使得深度缓冲区算法难以确定应该渲染两个表面中的哪一个(因为两者都不“最接近”相机)。发生这种情况时,浮点舍入误差可能会导致渲染表面的某些部分使用其中一个对象的颜色,而其他部分则使用另一个对象的颜色。这种不自然的伪影称为 Z冲突(Z-fighting)或深度冲突(depth-fighting),是渲染的片段在深度缓冲区中相互对应的像素条目上“斗争”的结果。
创建地形或阴影时经常会出现这种情况。在这种情况下,有时 Z 冲突是可以预知的, 并且校正它的常用方法是稍微移动一个物体,使得表面不再共面。
Z 冲突出现的原因还可能是深度缓冲区中的值的精度有限。对于由 Z-buffer 算法处理的每个像素,其深度信息的精度受深度缓冲区中可存储的位数限制。用于构建透视矩阵的近、远剪裁平面之间的距离越远,具有相似(但不相等)的实际深度的两个对象的点在深度缓冲区中的数值表示越可能相同。因此,程序员可以选择适当的近、远剪裁平面值来最小化两个平面之间的距离,同时仍然确保场景必需的所有对象都位于视锥内。
同样重要的是,由于透视变换的影响,改变近剪裁平面值可能比对远剪裁平面进行等效变化对于 Z 冲突伪影具有更大的影响。因此,建议避免选择太靠近相机的近剪裁平面。
本书前面的例子只是简单地(在我们对 perspective()的调用中)使用了 0.1 和 1000 作为近、远剪裁平面的坐标值。这些值可能需要针对你的场景进行调整。
图元的其他选项
OpenGL 支持许多图元类型。OpenGL 支持的图元如下:

性能优先的编程方法
随着 3D 场景的复杂性增加,我们将越来越关注性能。我们已经看到一些这样的例子:为了速度做出一些编程上的决策,例如使用实例化或将“昂贵”的计算转移到着色器。
❶尽量减少动态内存空间分配
将 display()函数的开销保持在最低限度的一个重要方法是避免任何需要内存分配的步骤。因此,明显要避免的步骤包括:
- 实例化对象;
- 声明变量。
我们实际上在调用 display()函数之前就已经声明了 display()函数中使用到的每个变量,并分配了相应的空间。声明或实例化几乎从不出现在display()函数中。例如,示例程序包含以下代码块:
// 分配在 display()函数中使用的变量空间,这样它们就不必在渲染过程中分配
GLuint mvLoc, projLoc;
int width, height;
float aspect;
glm::mat4 pMat, vMat, mMat, mvMat;
❷预先计算透视矩阵
可以减少 display()函数开销的另一个优化是将透视矩阵的计算移动到 init() 函数中。
❸背面剔除
提高渲染效率的另一种方法是利用 OpenGL 的背面剔除能力。 当 3D 模型完全“闭合” 时,意味着内部永远不可见(例如对于立方体和四棱锥),那么外表面的那些与观察者背离且呈一定角度的部分将始终被同一模型的其他部分遮挡。也就是说,那些背离观察者的三角形不可能被看到(无论如何它们都会在隐藏面消除的过程中被覆盖),因此没有理由栅格化或渲染它们。
我们可以使用命令 glEnable(GL_CULL_FACE) 要求 OpenGL 识别并“剔除”(不渲染)背向的三角形。我们还可以使用 glDisable(GL_CULL_FACE) 禁用背面剔除。默认情况下,背面剔除是关闭的,因此如果你希望 OpenGL 剔除背向三角形,必须手动启用它。
启用背面剔除时, 默认情况下, 三角形只有朝前时才会被渲染。 此外, 默认情况下, 从 OpenGL相机的角度看,如果三角形的 3 个顶点是以逆时针顺序排列的(基于它们在缓冲区中定义的顺序),则三角形被视为朝前;顶点沿顺时针方向排列的三角形是朝后的,不会被渲染。这种定义“前向”的顶点顺序有时被称为缠绕顺序,可以使用 glFrontFace(GL_CCW) 显式设置逆时针为正向(默认如此),或使用glFrontFace(GL_CW)设置顺时针为正向。类似地,也可以显式设置是否渲染正向或背向的三角形。实际上,为了达到这个目的,我们指定哪些三角形不被渲染,即哪些三角形被“剔除”。我们可以通过调用 glCullFace(GL_BACK)指定背向的三角形被剔除(尽管这是不必要的,因为它是默认的),或者通过用 GL_FRONT 和 GL_FRONT_ AND_BACK 替换参数 GL_BACK 来分别指定剔除前向三角形和所有三角形。
3D 模型通常被设计成外表面由相同缠绕顺序的三角形构成。如果启用剔除,则默认情况下模型的外部面向相机的表面部分会被渲染,因为默认情况下 OpenGL 假定的缠绕顺序是逆时针方向;如果模型设计缠绕顺序为顺时针方向,那么如果启用了背面剔除, 需要由程序员调用 gl_FrontFace (GL_CW)来解决剔除部分不正确
的问题。
注意,在 GL_TRIANGLE_STRIP 的情况下,每个三角形的缠绕顺序不停地互换。 OpenGL 通过在连续构建三角形时不断“颠倒”顶点顺序来补偿这一点,如依次使用 0-1-2、 2-1-3、 2-3-4、4-3-5、 4-5-6 等顶点组合构建三角形。
背面剔除通过确保 OpenGL 不花时间栅格化和渲染从不被看到的表面来提高性能。我们在本章中看到的大多数示例都非常小,以至于没有必要进行背面剔除(对于实例化 100000 个多边形动画实例,可能会对某些系统造成性能挑战)。在实践中,大多数 3D 模型通常是“闭合的”,因此习惯上会常规地启用背面剔除。例如,我们可以通过修改 display()函数向示例程序添加背面剔除:
void display(GLFWwindow* window, double currentTime) {
...
glEnable(GL_CULL_FACE);
// 绘制立方体
...
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glFrontFace(GL_CW);// 立方体顶点的缠绕顺序为顺时针方向
glDrawArrays(GL_TRIANGLES, 0, 36);
// 绘制四棱锥
...
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_LEQUAL);
glFrontFace(GL_CCW);// 四棱锥顶点缠绕顺序为逆时针方向(默认)
glDrawArrays(GL_TRIANGLES, 0, 18);
}
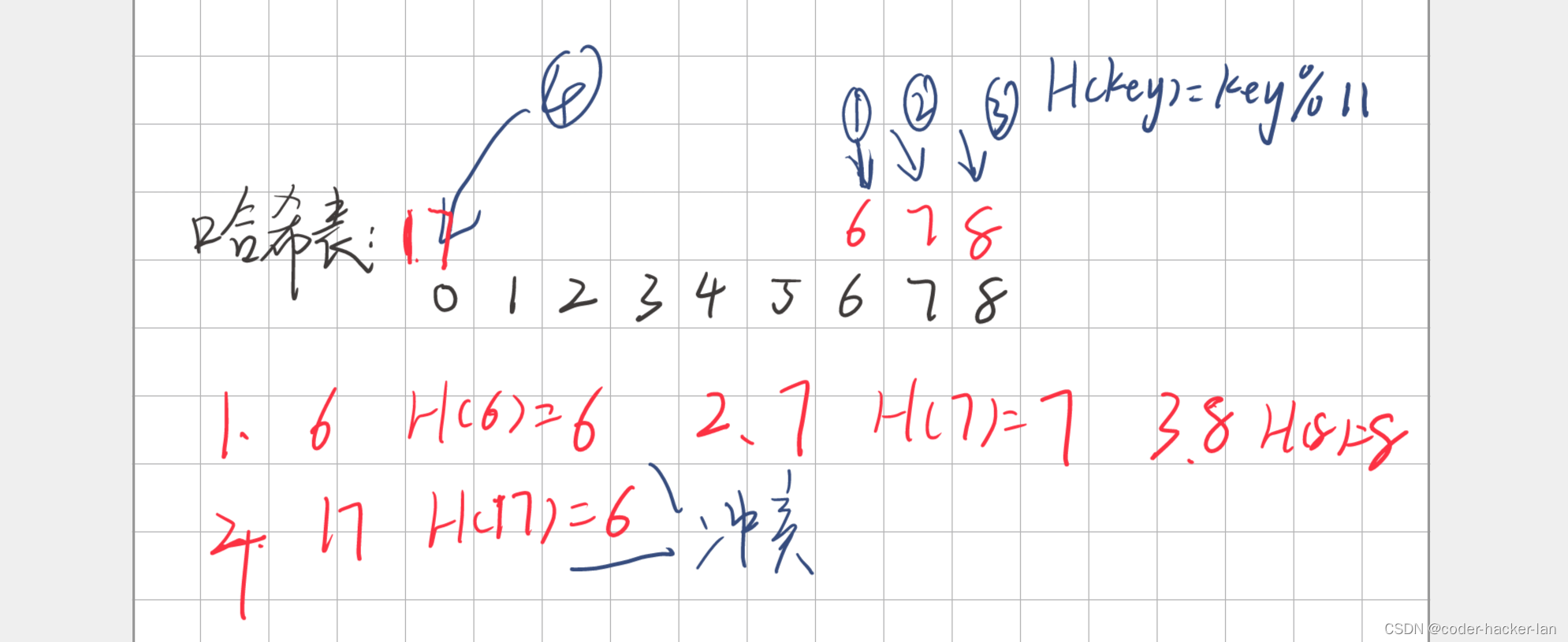




![[足式机器人]Part4 南科大高等机器人控制课 Ch08 Rigid Body Dynamics](https://img-blog.csdnimg.cn/direct/1677268e1f9f4a919827801b77b5c093.png)